基于几何学的无线传感器网络节点定位算法研究

陶琳， 杨俊成， 杨新锋

(1.河南工业职业技术学院 电子信息工程系， 南阳 473003 2.南阳理工学院 计算机与信息工程学院， 南阳 473003)

基于几何学的无线传感器网络节点定位算法研究

陶琳1， 杨俊成1， 杨新锋2

(1.河南工业职业技术学院 电子信息工程系， 南阳 473003 2.南阳理工学院 计算机与信息工程学院， 南阳 473003)

将几何学中的斜率概念引入到无线传感器网络定位算法中，提出了一种分析锚节点之间位置关系的方法，并给出了一种基于几何学的定位方案。在二维平面上定位一个目标节点需要3个位置已知的锚节点，这3个锚节点的选取是非常重要的，如果未知节点所选取的锚节点位置不合理将无法定位出节点的位置，因此，节点在定位前根据提出的方案选出最优的锚节点组合，然后再进行定位，可以提高定位的准确性。为定位算法中锚节点的选取提供可靠依据，从而达到了提高定位精度和定位覆盖率的效果。

无线传感器网络； 节点定位； 几何学； 斜率

0 引言

无线传感器网络WSN(wireless sensor network)是一种由许多微型传感器节点组成的自组织网络，这些传感器节点集成数据采集、数据处理和无线通信等功能，且它们具备制作成本低、功耗低、体积微小等特点，WSN已经成为一种新型的信息获取和处理技术[1]。传感器节点采集监测区域内的感知信息，通过中间节点进行一系列处理，并以多跳的方式传输给汇聚节点实现网络自动监测；同时汇聚节点也可以向网络中的传感器节点传输控制指令来执行特殊任务。无线传感器网络改变了人类与自然界的交互方式，扩大了人类认知世界的能力[2]。美国商业周刊将无线传感器网络誉为21世纪最具有影响力的21项技术和改变世界的十大技术之一[3]。

无线传感器网络中每个传感器节点搜集到监测的数据之后，通过无线通信的方式发送给汇聚节点，最终传输给管理者。在处理数据的过程中，最重要的是我们要知道数据的来源，是哪个位置的传感器发来的数据，从而为用户提供最有意义的数据[4]。传感器节点可以配备GPS定位系统来获得自身的绝对位置，但是受体积、价格和能耗的影响[5],每个节点都使用GPS系统并不适合于无线传感器网络[6]。在本文中，网络中仅仅设置少量位置已知的节点，记为锚节点，其它节点是通过这些已知节点的位置信息，基于一些定位算法来获得自身位置坐标，所以开发简单和准确的定位算法是研究者的追求目标。

1 WSN定位技术的研究现状

为了估计出未知节点的位置，锚节点与未知节点需要通过无线通信的方式彼此交互信息。由此产生两种定位技术[7]：一种是基于测距的定位技术，利用硬件设备，例如超声波、无线电和天线阵列等获得节点之间的信号强度、到达时间以及到达角度，利用这些参数计算出未知节点到达锚节点的真实距离，从而估计未知节点的位置，是一种高精度的定位方法[8]；另一种是非测距的定位技术，利用网络中的锚节点信息和网络的连通度，间接得到锚节点与未知节点的距离，这种方法不需要测得节点间的真实距离，是一种粗粒度定位的方法。通过以上两种方法得到了锚节点到未知节点的距离之后，采用位置计算的数学方法计算出节点的位置。

基于测距的定位算法的是依据锚节点到目标节点的距离或者角度进行定位。目前，具有代表性的定位算法有基于到达角度(Angle of Arrival, AOA)、基于到达时间(Time of Arrival, TOA)、基于到达时间差(Time difference of Arrival, TDOA)和基于信号接收强度指示(Received Signal Strength Indicator, RSSI)的定位方法。非测距定位算法是一种粗粒度定位估计方法，对于无线传感器网络某些应用也是可以满足的，是一种追求低成本的定位技术，因此，这种方法也备受关注。目前，典型的非测距定位算法包括APS(DV-Hop、DV-distance、Euclidean)、APIT、Centroid、Amorphous等，在这些方法的基础上，广大学者针对非测距定位算法提出了新的定位方法。

2 几何学定位算法描述

为更好地利用锚节点的信息，本文提出一种基于几何学的定位算法。首先，我们使用几何学中的斜率方法，即用斜率来判断锚节点之间的分布关系。其次，又分析了当锚节点个数为3个和大于3个的时候，分别采用的不同方法来求解未知节点的位置。

2.1 模型建立

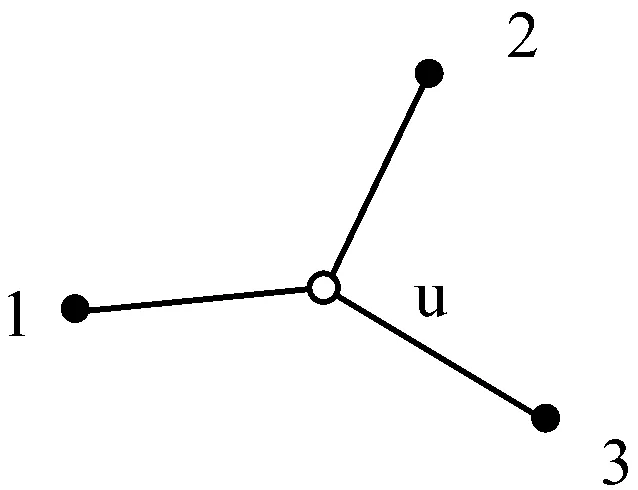
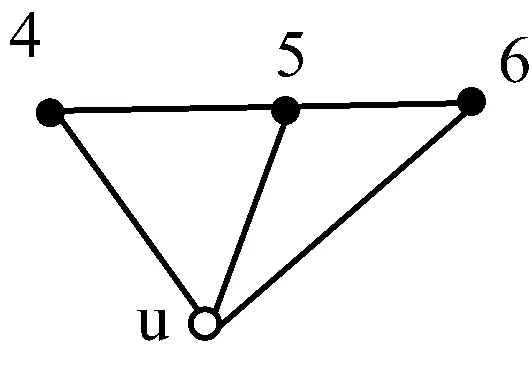
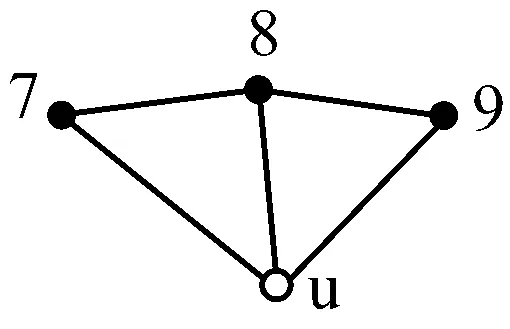
无线传感器网络定位的数学模型描述如下：假设设置m个传感器节点(锚节点)，并且每个节点都知道自己的位置，二维空间坐标αk∈R2，k=1,2,…,m。n个传感器节点(非锚节点)xj∈R2，j=1,2,…,n，这些节点称为未知节点。在一个二维空间中，要想实现一个目标的定位，最少需要3点才能够确定目标的位置。在二维平面中，两个节点在平面的分布关系可以用斜率值表示，判断任意一点与其它两个点连线角度关系用斜率差表示，如图1所示(如图1(a)所示)。

3个黑色节点1、2、3为锚节点，空心u为未知节点，3个锚节点可以很容易求出未知节点u的位置。图1(b)中锚节点4、5、6在同一条直线上，那从几何角度考虑，这种分布的点是无法解出未知点u。图1(c)中锚节点7、8、9虽然不是在一条直线上，但是趋近于直线，如果测距存在误差，可能造成无法解出未知节点u。因此，本文提出一种方法来选取一种相对最优的锚节点组合。

(a)

(b)

(c)

2.2 锚节点最优组合选择

在无线传感器网络中，DV-Hop属于非测距的定位算法，不需要借助外在的硬件设备测量锚节点到未知节点的真实距离，从而减少了节点的成本开销和能量消耗，此算法简单、覆盖度高和可行性好，所以这种定位算法被很多学者所青睐，在应用中是最有潜力的一种定位算法。但由于DV-Hop算法在锚节点位置选择上不一定是最优的，会造成未知节点无法定位，尤其是未知节点接收到超过3个锚节点时，如果3个锚节点在一条直线节点将无法求解，严重影响网络的整体定位精度。然而平面几何学中的斜率方法可以判断锚节点之间的位置关系，从而选取最优的锚节点序列，能够更精确的确定未知节点的位置。同时分析了待定位节点的邻居锚节点数量对定位精度的影响。

算法的具体步骤如下：

步骤1：网络初始化

步骤2：计算网络中所有锚节点的平均每跳距离值，并进行广播

步骤3：未知节点对锚节点的选取。当网络中的未知节点接收到锚节点平均每跳校正值时，判断锚节点的个数，判断的具体过程描述如下：(1)当锚节点数目小于3时，无法执行最小二乘定位；(2)当锚节点等于3时，判断3点是否接近共线，如图4.3所示，首先计算直线L1L2的斜率为K1，再计算直线L2L5，的斜率K2，当K2-K1的值越接近0的时候，3点越接近共线，利用这3个点计算未知节点的位置就不准确了，重新选择锚节点；(3)当锚节点大于3时，首先选取最先接收到锚节点的信息作为参考节点，在从其余的锚节点中选取两个锚节点进行定位，进行多次求出未知节点的位置，再把求出的位置求均值。如图2所示。

如果待定位节点同时收到锚节点L1，L2，L3，L4，L5发送的信息包时，待定位节点将最先接收到L1的消息，把L1作为参考节点，分别从其它锚节点中选出两个锚节点，构成3个锚节点，反回步骤(2)判断3个锚节点是否共线。

几何学算法的具体流程，如图3所示。

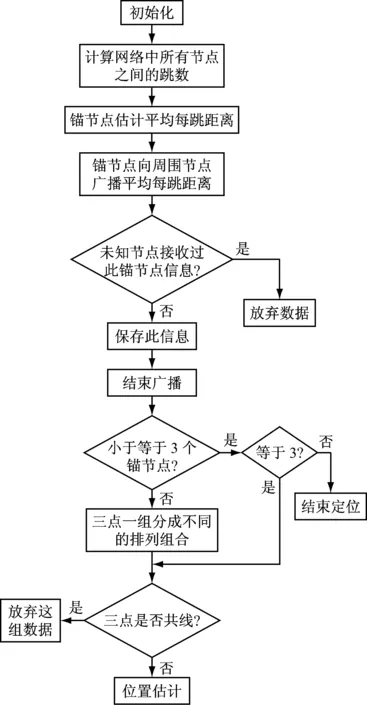
图3 几何学算法流程

算法的初始化阶段和平均每跳距离的求解步骤与DV-Hop算法相同，只有在选择锚节点定位时本文采取斜率判断法来获得最优的锚节点组合，从而实现精准的定位。

2.3 位置估计

最后，根据最小二乘法估计出未知节点A的位置。以L1作为参考节点，分别从其它四个锚节点中选出两个节点构成最小二乘定位，求出未知节点A的坐标，一共有6种组合，求出未知节点A有6个坐标A1(x1,y1)，A2(x2,y2)，A3(x3,y3)，A4(x4,y4)，A5(x5,y5)，A6(x6,y6)，之后对这六个坐标求平均，得到A(xreal,yreal)。

3 仿真测试

(1)网络场景设置

使用MATLAB对无线传感器网络DV-Hop定位算法以及本文所提出的定位算法进行仿真，研究整个网络中锚节点之间的位置关系和所选锚节点数量的最优组合对网络性能的影响。实验中采用的网络拓扑结构：锚节点和未知节点都是随机产生，锚节点分布在网络中不同的位置。仿真参数设置为：网络范围100 m×100，节点数目100个，传输距离为10 m、20 m及30 m，锚节点个数为10、15、20、25、30、35、50。

(2)仿真结果与分析

随着锚节点数量的增加，本文的几何学定位算法定位误差逐渐下降。图4为网络的拓扑结构图，如图4所示。

图4 网络节点分布图

星节点为锚节点，当随机播撒节点的时候，有些锚节点排列成直线分布，在一条直线上的3个点是无法定位出一个点的位置的，这样用原始的DV-Hop算法定位，误差将会很大。

仿真的横坐标代表锚节点的个数;纵坐标为节点的定位精度，即平均定位误差与通信半径的百分比。实验结果表明，随着通信半径的增加，锚节点数目相同的情况下，确实改进了网络定位精度。

如图5所示:

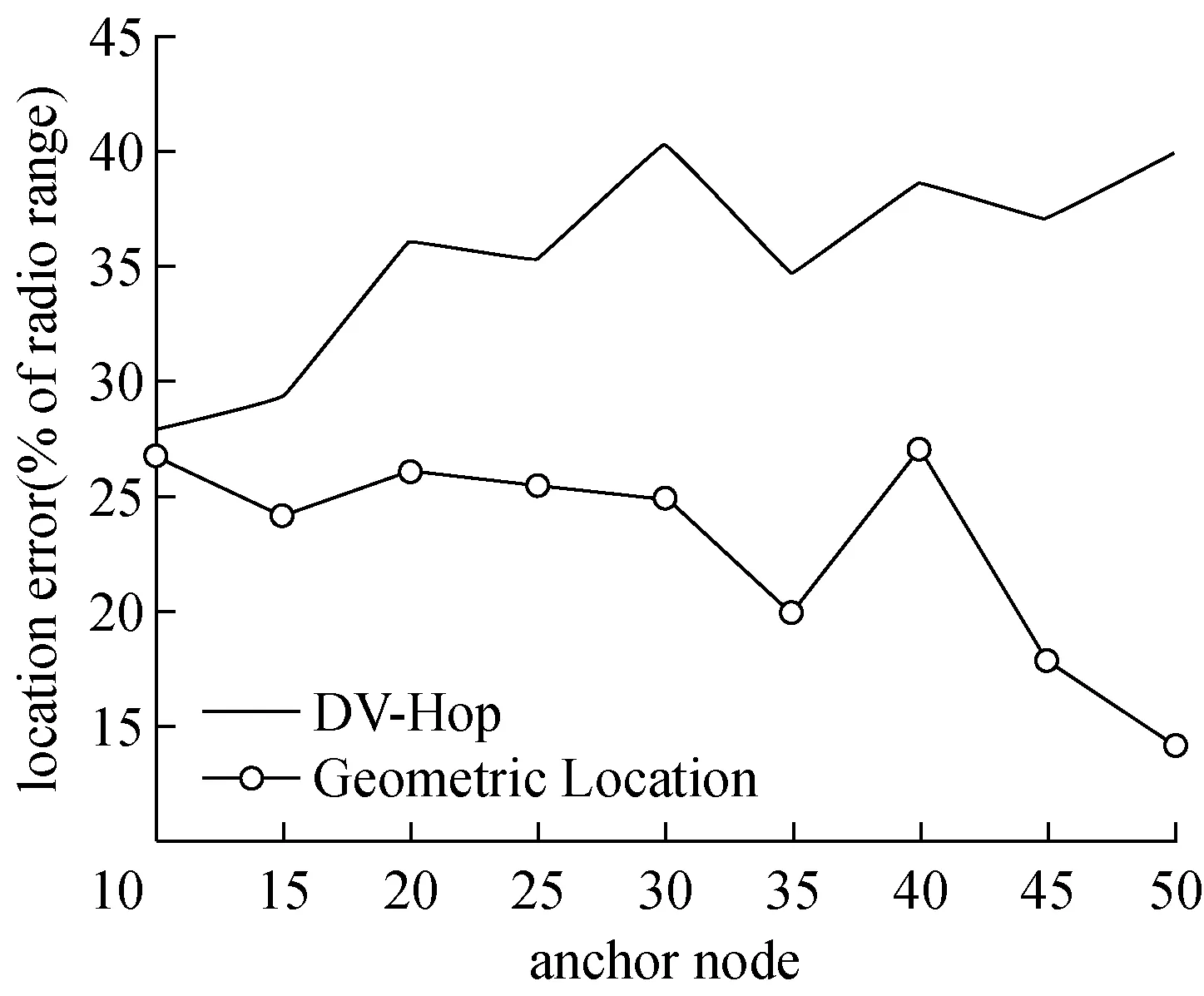
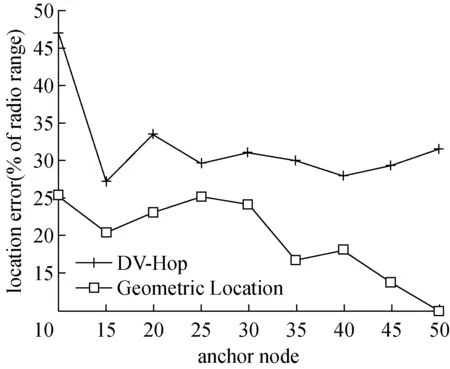
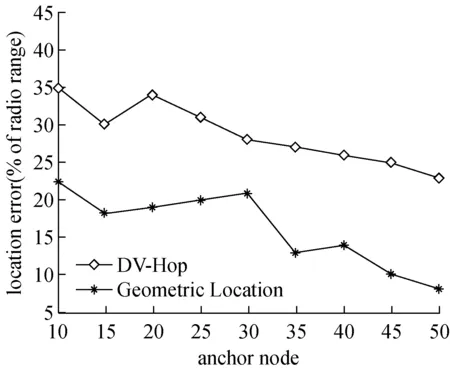
图5(a)、(b)和(c)表示通信半径R=10、20、30时本文定位算法(Geometric Location)与DV-Hop定位算法误差的对比。在不同通信半径下本文算法(Geometric Location)的定位误差变化，如图6所示。锚节点大于25时定位误差明显下降，如图6所示。

如图7所示。

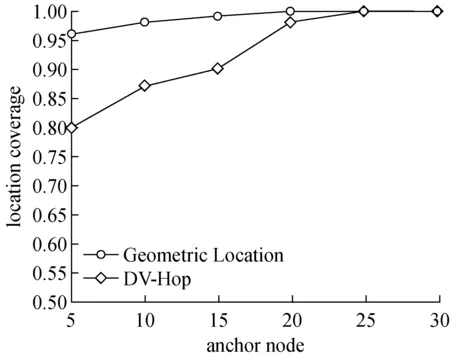
图7(a)、(b)和(c)表示表示通信半径R=10、20、30时本文定位算法(geometric location)与DV-Hop定位算法定位率的对比，证明了通信半径增加，可以提高定位率。在不同的通信半径下本文定位算法(geometric location)定位率的变化关系，如图8所示。

随着锚节点增多本文算法的定位率在逐渐的提升。

(a)通信半径R=10

(b)通信半径R=20

(c)通信半径R=30

图6 不同通信半径下Geometric Location的定位误差对比

(a)通信半径R=10

(b)通信半径R=20

(c)通信半径R=30

图8 不同通信半径下Geometric Location的定位率对比

4 总结

在无线传感器网络中，无论是基于测距的定位技术还是非测距定位技术锚节点的信息都是一个不可或缺的重要因素。本文将几何学中的斜率概念引入到了无线传感器网络定位算法中，分析锚节点之间的位置关系对定位精度的影响，并给出一种基于此方法的定位方案。当未知节点定位时需对所选择的锚节点组合进行分析处理，根据斜率判断锚节点是否趋于一条直线或者未知节点与锚节点是否在一条直线，是则放弃，直到选出最优的锚节点组合；其次分析了待定位节点的邻居锚节点数量对该定位算法定位精度的影响，提出了基于几何学中斜率的方法找出锚节点最优组合的选择策略，在不同的通信半径下，该策略的定位精度和定位率相比DV-Hop定位算法都有很大的提升。此方法为定位算法中锚节点的选取提供可靠依据，从而达到了提高定位精度和定位覆盖率的效果。

[1] 郑增威, 吴朝晖, 金水祥. 无线传感器网络及其应用[J]. 计算机科学, 2003, 30(10): 138-140.

[2] 马祖长, 孙怡宁, 梅涛. 无线传感器网络综述[J]. 通信学报, 2004, 25(4): 114-124.

[3] 刘刚, 周兴社, 谷建华等. 自组织、自适应无线传感器网络理论研究[J]. 计算机应用研究, 2005, 5: 30-33.

[4] Martusevicius V, Kazanavicius E. Self-localization system for wireless sensor network[J]. Elektronika Ir Elektrothchnika, 2010, 16(10): 17-20.

[5] Guoqiang Mao, Baris Fidan, Brian D.O.Anderson. Wireless sensor network localization techniques[J]. Computer Networks, 2007, 51(10): 2529-2553.

[6] Randolph L Moses, Dushyanth Krishnamurthy, Robert Patterson. A self-localization method for wireless sensor networks[J]. EURASIP Journal on Applied Signal Processing, 2003(4): 348-358.

[7] Chen J C, Hudson R E, Yao K. Maximum-likelihood source localization and unknown sensor location estimation for wideband signals in the near-filed[J]. IEEE Transaction on Signal Processing, 2002, 50(8):1843-1854.

[8] 刘影, 钱志鸿, 刘月一, 张旭. 基于几何学的无线传感器网络定位算法[J]. 光电子·激光期刊, 2010, 10(21):1435-1438.

Research on Wireless Sensor Network Node Localization Algorithm Based on Geometry

Tao Lin1,Yang Juncheng1,Yang Xinfeng2

(1. Department of Electronic Information Engineering,Henan Polytechnic Institute,Nanyang 473004,China;2. School of Computer and Information Engineering,Nanyang Institute of Technology,Nanyang 473004,China)

It was the first time that the gradient concept of geometry was applied to the wireless sensor network localization algorithm. The method for analyzing the position relationship between anchor nodes has been investigated and given by the location of geometric algorithm. In two-dimensional plane, locating a target node requires three anchor nodes which have a significant selected position. If the selected anchor node doesn’t fit, this cannot locate the position of unknown node. Therefore, before localization, the optimum anchor node combination should be selected in accordance with the proposed scheme, and then locating these nodes can improve the accuracy of localization. This method provides reliable basis for the selection of anchor nodes in localization algorithm, and then improves location accuracy and location coverage.

Wireless sensor network; Node localization; Geometry; Gradient

河南省科技攻关重点计划项目(112102210500)

陶 琳(1979-)，女，河南南阳人，工程硕士，讲师，研究方向：计算机应用，南阳 473003 杨俊成(1982-)，男，河南南阳人，硕士，讲师，研究方向：人工智能、嵌入式系统，南阳 473003 杨新锋(1979-)，男，河南南阳人，硕士，副教授，研究方向：图像处理，南阳 473003

1007-757X(2017)01-0026-04

TP393

A

2016.05.10)