基于GSPN和蒙特卡罗仿真的软件可靠性研究

冷令, 吴伟斌

(1. 中山职业技术学院， 中山 528400； 2. 华南农业大学工程学院， 广州 510642)

基于GSPN和蒙特卡罗仿真的软件可靠性研究

冷令1, 吴伟斌2

(1. 中山职业技术学院， 中山 528400； 2. 华南农业大学工程学院， 广州 510642)

提出了一种基于广义随机Petri网(Generalized Stochastic Petri Net，GSPN)和蒙特卡罗仿真的软件可靠性建模与分析方法。在探讨GSPN模型要素图符表示及用法的基础上，给出了基于GSPN的软件可靠性建模流程。以软件可靠性分析GSPN模型基础，采用蒙特卡罗仿真方法对模型中库所、变迁持续时间等参数进行统计，计算软件的可用度参数。实例研究验证了所提方法的有效性，该方法可以为软件可靠性分析与设计提供有益参考。

软件； 广义随机Petri网； 蒙特卡罗仿真； 可靠性

0 引言

软件可靠性建模与分析是软件开发与设计过程中的关键环节之一。传统分析方法存在诸多不足[1]，如：故障树等模型不能模拟软件动态特性，Markov链等模型虽然能模拟软件动态特性，但模型可解算性较差。近年来，广义随机Petri网(generalized stochastic Petri net，GSPN)[2]在模拟软件可靠性动态行为方面表现出了良好的性能[3-5]，但是由于模型大多复杂也无法克服状态空间爆炸的问题。蒙特卡罗仿真方法[6-8]在系统可靠性分析中能够适应各种规模的系统可靠性求解，弥补了GSPN在可靠性参数求解方面的不足。

本文目的在于研究一种基于GSPN和蒙特卡罗仿真的软件可靠性分析方法，以期为相关研究提供新思路。

1 基于GSPN的软件可靠性建模

1.1 GSPN定义

一个广义随机Petri网系统可以记为GSPN=(P,T,I,O,H,M0,W,λ)，其中：

(1)P={P1,P2,…,Pn}为库所的有穷集合；

(2)T={T1,T2,…,Tm}为变迁的有穷集合；

(3)I⊆P×T为输入弧的有穷集合；

(4)O⊆T×P为输出弧的有穷集合；

(5)H为禁止弧的有穷集合；

(6)M0为系统初始标识的集合；

(7)W为弧权函数的有穷集合；

(8)λ={λ1,λ2,…,λm}为变迁的平均实施速率。时间变迁中λ为变迁所服从的泊松分布参数；瞬时变迁中λ为变迁实施概率值。

1.2 GSPN模型要素图符表示及用法

GSPN模型要素的图符表示及用法[11-12],如表1所示。

1.3 建模流程

软件可靠性的GSPN建模的具体步骤如下：

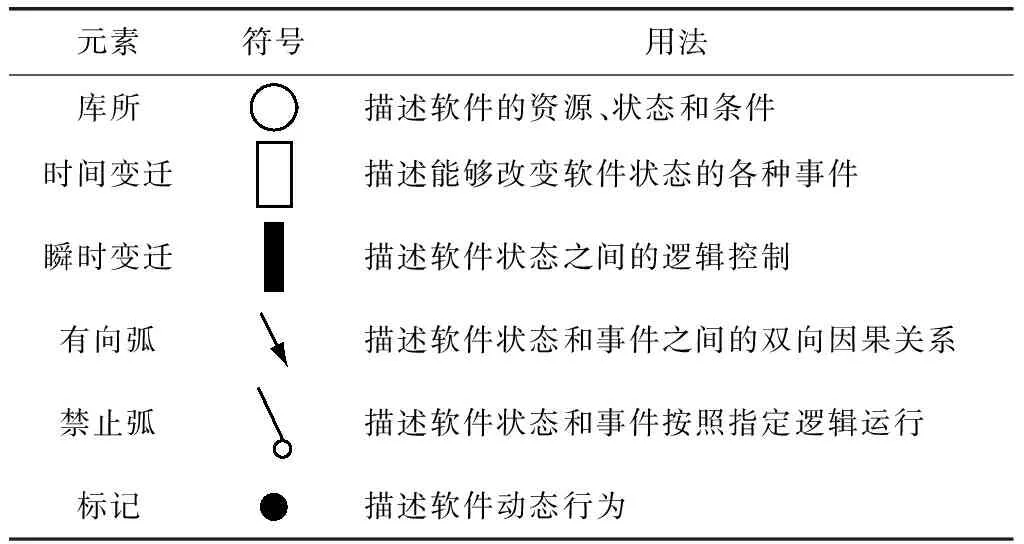
表1 GSPN模型要素图符表示及用法

(1) 深入分析软件的功能结构，将软件分解为若干逻辑关系组合的功能模块。

(2) 根据软件中各功能模块间的连接与因果逻辑关系，建立软件的可靠性框图模型。

(3) 应用GSPN描述软件的可靠性框图模型，构建基于GSPN的软件可靠性分析模型。

(4) 根据软件中构件的故障率和维修率，设置GSPN模型相应的参数，采用蒙特卡罗仿真方法分析求解软件的可用度。

2 基于蒙特卡罗仿真的软件可用度计算

GSPN模型可以有效地刻画软件的动态行为及其演化过程，为计算软件可靠性参数提供了条件[9-10]。如图1所示。

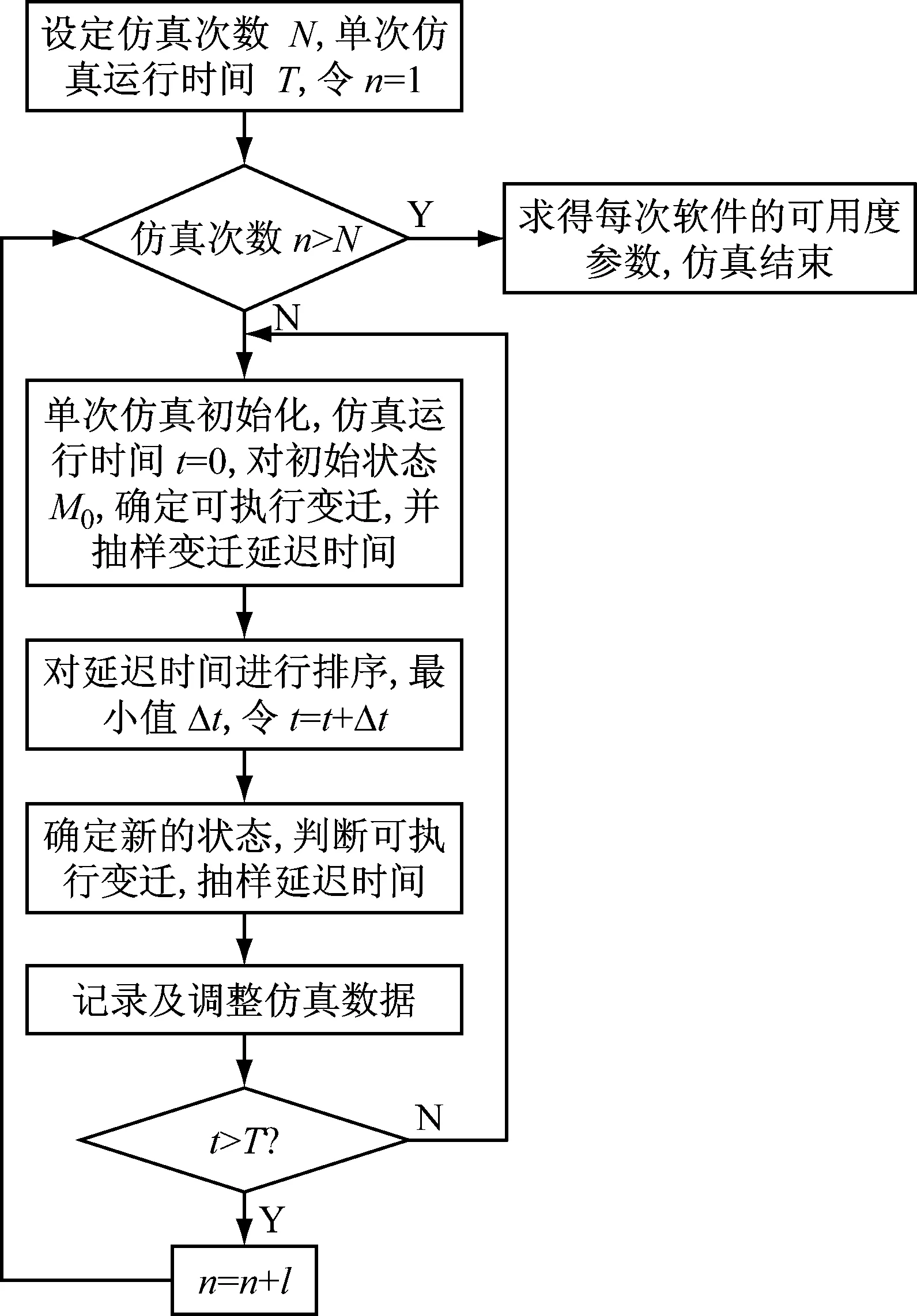
图1 基于蒙特卡罗仿真的软件可用度计算流程

本文采用蒙特卡罗仿真方法统计软件可靠性分析GSPN模型中库所、变迁、软件状态的持续时间，进而计算软件平均无故障工作时间MTBF、平均维修时间MTTR及可用度As等参数，相应计算公式分别为式(1)、式(2)和式(3)。

(1)

(2)

(3)

其中：Mi表示软件处于故障状态i；tn表示第n次仿真所消耗的时间；t(Mi)表示软件处于故障状态i的持续时间；Pi表示软件处于故障状态i的概率；Mni表示第n次仿真中软件处于故障状态i；t(Mni)第n次仿真中软件处于故障状态i的持续时间；f(Mni)表示第n次仿真中软件处于故障状态i的次数。

3 实例研究

本小节选择某工程软件服务流程作为研究对象，考察本文方法的有效性。该软件服务流程中包括S1、S2、S3、S4、S5和S6共6个软件子服务，其中软件子服务S2和S5属于同类型服务，共用一种异常处理模式进行修复。按照所提方法的步骤，建立的可靠性框图模型，如图2所示。

图2 某软件服务流程可靠性框图模型

在保证所建GSPN模型正确有效的基本前提下，做以下假设：

(1) 以软件子服务为建模基本单元，不做进一步更加细的划分。

(2) 仅考虑软件故障和正常两种工作状态。

(3) 软件故障服从故障率为λ=1/MTBF的泊松分布。

(4) 软件异常处理模式健全，软件故障后即时处理，服从维修率为μ=1/MTTR的泊松分布，且修复如新。

基于上述假设，根据该软件服务流程可靠性框图，建立其可靠性分析GSPN模型，如图3所示。

图3中：库所Psf表示软件整体处于故障状态；库所Pwi(i=1,2,…,6)表示软件子服务Si处于正常状态；库所Pfi(i=1,2,…,6)表示软件子服务Si处于故障状态；库所Pr表示软件子服务S2和S5的共用异常处理机制的使用权；库所Pcri(i=2,6)表示软件子服务Si的异常处理机制处于可用状态；时间变迁Tfi(i=1,2,…,6)表示软件子服务Si发生故障；时间变迁Tri(i=1,2,…,6)表示软件子服务Si的故障被修复；瞬时变迁Tsfi(i=1,2,…,6)表示软件子服务Si发生故障导致软件整体故障；瞬时变迁Tcri(i=2,6)表示软件子服务Si的异常处理机制可以进行工作；各软件子服务的故障率与维修率，如表2所示。

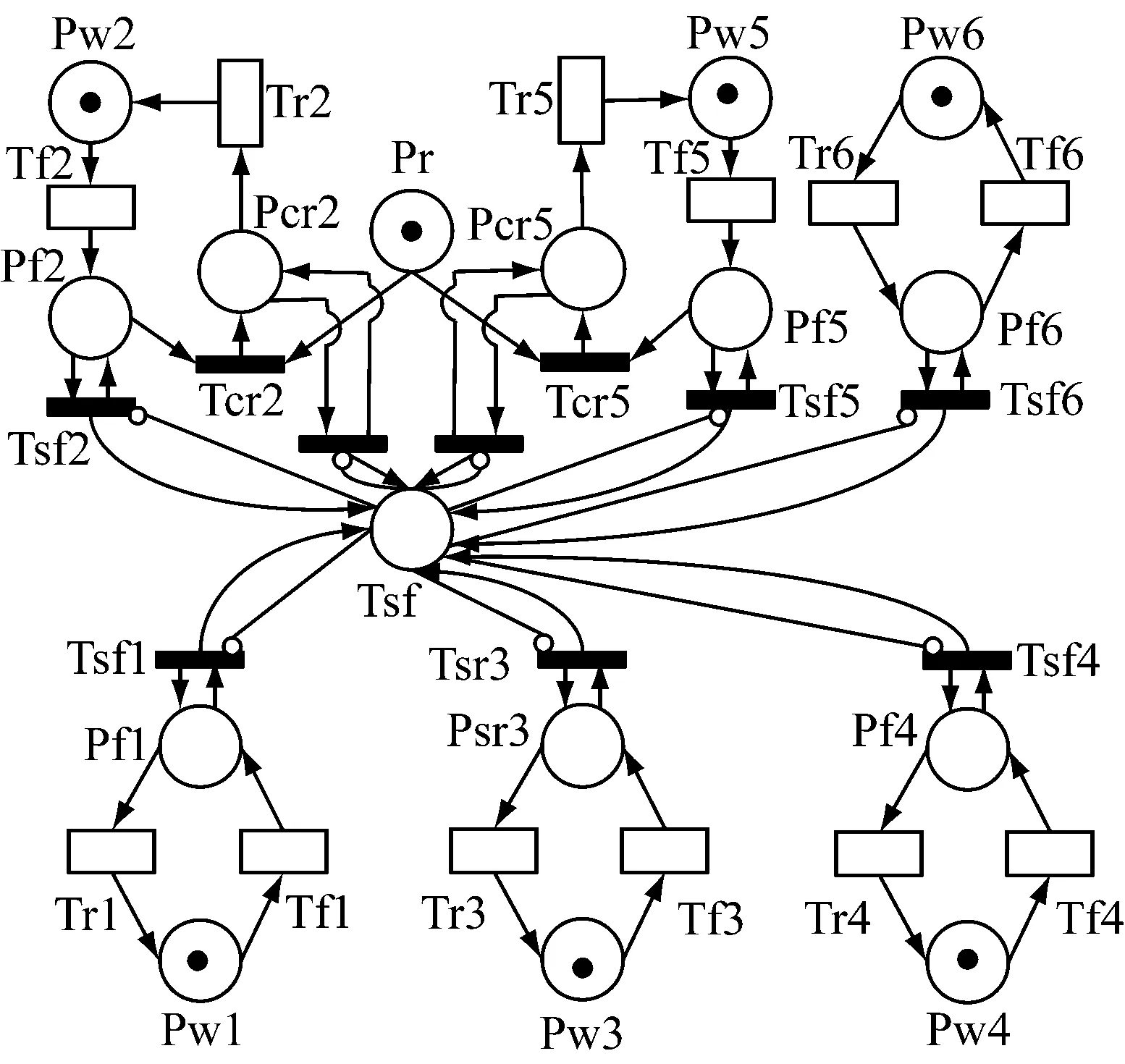
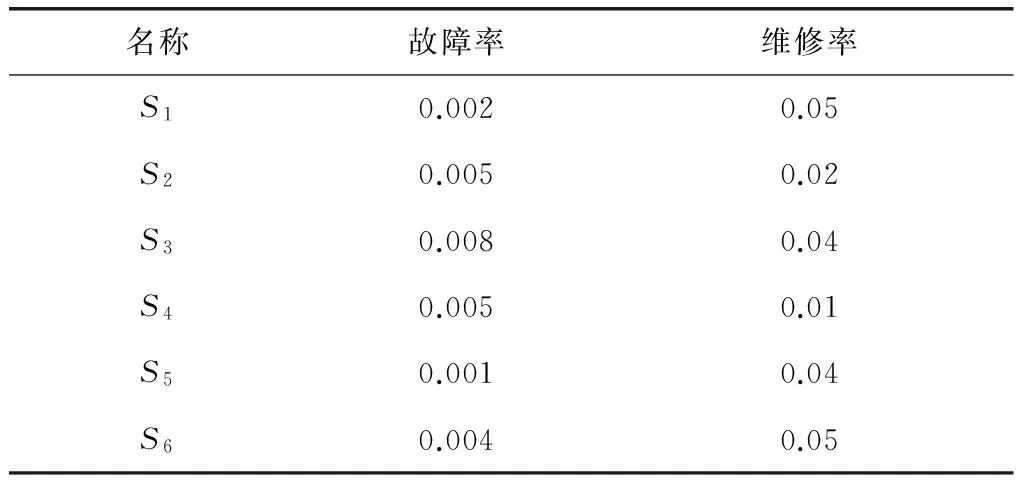
图3 某软件服务流程可靠性分析GSPN模型

在Matlab 2011a软件环境[9]下，对该软件服务流程进行蒙特卡罗仿真，进而得到软件可用度变化曲线，如图4所示。

图4 某软件服务流程可用度曲线

由仿真结果可知：该软件服务流程可用度曲线在时间段0≤t≤50 h内,随着时间的增加迅速下降，从100%到80.3%；当时间t≥50 h以后，系统的可用度大致趋于平稳，但略有微小浮动，最后为79.5%。这是由于该软件服务流程的故障时候各个软件子服务的故障累加的结果，因此在设计软件流程时，应尽量采用精化设计，减少没必要的软件子服务。

4 总结

本文提出了一种基于GSPN和蒙特卡罗仿真的软件可靠性分析方法，该方法可以有效地模拟软件的动态行为。在建立软件可靠性分析GSPN模型的基础上，采用蒙特卡罗仿真方法可以快速计算软件的可用度参数。以某工程软件服务流程为例，仿真验证了所提方法的有效性。下一步将结合智能算法研究各个软件子服务在不同故障率和维修率分布条件下的可用度参数变化规律。

[1] 王少萍. 工程可靠性[M]. 北京:北京航空航天大学出版社, 2000:18-42.

[2] 林闯. 计算机网络和计算机系统的性能评价[M]. 北京:清华大学出版社, 2001:133-162.

[3] 苏春. 基于GSPN模型的系统动态可靠性仿真研究[J].航空学报,2006,19(1):1-5.

[4] 石健, 王少萍, 王康. 基于GSPN的机载液压作动系统可靠性模型[J].航空学报,2011,32(5):920-933.[5] 谷春英, 姚青山. 基于GSPN的计算机硬件系统可靠性分析[J].微电子学与计算机,2013,30(6):122-126.[6] 肖刚, 李天柁. 系统可靠性分析中的蒙特卡罗方法[M].北京：北京科学出版社,2003:32-76.

[7] 王圣金, 苏春, 许映秋. 基于Petri网和蒙特卡洛仿真的液压系统可靠性研究[J].机械科学与技术,2006,25(10):1206-1237.

[8] 李世毅, 马振利, 张承良,等. 广义随机Petri网和Monte Carlo仿真在系统可靠性分配中的应用[J].科学技术与工程,2010,36:9035-9038.

[9] 张志涌. 精通Matlab 2011a[M].北京：北京航空航天大学出版社 ，2011:150-233.

[10] 戴志辉,王增平,焦彦军. 基于动态故障树与蒙特卡罗仿真的保护系统动态可靠性评估[J]. 中国电机工程学报. 2011(19)：107-115.

[11] 陈克伟,董利霞,李丹. 基于GSPN的网络系统动态可靠性建模方法[J]. 计算机测量与控制. 2012(04)：1091-1094.

[12] 吴恒润.计算机硬件系统维护原则与方法讨论[J]. 无线互联科技,2013(12)：97-98.

Research on Software Reliability Based on Generalized Stochastic Petri Net and Monte Carlo Simulation

Leng Ling1,Wu Weibin2

(1. Zhongshan Polytechnic Institute,Zhongshan 528400,China;2. College of Engineering,South China Agricultural University，Guangzhou 510642,China)

This paper presents a new reliability analysis method for software based on generalized stochastic petri net(GSPN) and Monte Carlo simulation. By discussing the model element icons and their usage of GSPN, the reliability of modeling process of software based on GSPN is given. On the basis of reliability analysis of GSPN model for software, Monte Carlo simulation is used to obtain statistical parameters of duration time of transition and places, and calculate the availability of software. A certain engineering software is used to validate the proposed method. The work of this paper can provide theoretical guidance for the reliability analysis and design of software.

software; generalized stochastic petri net; Monte Carlo simulation; reliability

“十二五”农村领域国家科技计划项目(2014BAD16B0103)；2015年度国家星火计划(2015GA780063)；广东省省级科技计划项目(2014A070713032)

冷令(1980-)，男，辽宁沈阳人，硕士，信息系统项目管理师/讲师，研究方向：计算机网络技术, 广州 528400； 吴伟斌(1978-)，男，广东中山人，博士，教授，硕士生导师，中国农业工程学会高级会员(E041200601S)，研究方向：农业工程、机电一体化和信息技术应用研究。广州 510642

1007-757X(2017)01-0009-03

TP391

A

2016.08.08)