BTT导弹状态反馈H∞控制自动驾驶仪设计

屈秀敏，刘珊中，刘永斌

（河南科技大学信息工程学院，河南洛阳471023）

BTT导弹状态反馈H∞控制自动驾驶仪设计

屈秀敏，刘珊中，刘永斌

（河南科技大学信息工程学院，河南洛阳471023）

针对倾斜转弯（BTT）导弹自动驾驶仪的抗干扰性和鲁棒性问题，以考虑耦合的情况下建立的更接近于实际的导弹数学模型为基础，将通道间的耦合作为干扰，在弹道特征点上对导弹模型进行解耦和线性化，得到各个通道的数学模型；设计基于线性矩阵不等式（LMI）的状态反馈H∞控制自动驾驶仪，搭建全耦合状态下的三通道仿真模型，并进行联合仿真研究。结果表明所设计的状态反馈H∞控制自动驾驶仪能够实现对导弹制导指令的有效跟踪，满足BTT导弹控制的要求。

倾斜转弯导弹，状态反馈H∞控制，线性矩阵不等式，自动驾驶仪

0 引言

倾斜转弯（BTT）技术因其具有快速大空域机动、升组比高、兼容性好、气动稳定性好、有利于开发新的气动导弹外形布局和载机的保形外挂等优点得以迅速发展［1］。BTT导弹作为一个具有非线性、时变、不确定和强耦合等特点的研究对象，其跟踪性能提高的主要困难来自空气动力参数和耦合等不确定性影响，因此，提高自动驾驶仪的鲁棒性成为提高导弹跟踪性能的关键问题。

传统的导弹自动驾驶仪是通过频域法和根轨迹法对每个通道独立设计，最后，经过反复调试参数实现对导弹的姿态控制［2-3］。在智能控制方面，基于反馈线性化和神经网络设计的自动驾驶仪，可以使具有不确定性的BTT导弹系统获得要求的跟踪性能，较好地控制侧滑角［4］。文献［5］设计了BTT导弹H∞鲁棒自动驾驶仪，通过仿真验证了控制器的性能，但设计过程中仅考虑了测量噪声对系统的影响，并没有分析系统中存在的其他不确定性。文献［6-7］将鲁棒控制与自适应控制相结合构成的控制器用于导弹姿态控制系统中可达到很好的效果。文献［8-9］将模糊和滑模变结构控制相结合后，控制算法简单，对模型的不确定性和外部干扰具有较强的鲁棒性，同时又能改善系统的控制性能。H∞控制是为多输入多输出（MIMO）且具有模型摄动的系统，提供的一种频域的鲁棒控制器设计方法，其最大特点是鲁棒性好［11］。本文在考虑耦合的情况下，建立更接近于实际的数学模型，并设计状态反馈H∞控制自动驾驶仪，进行耦合状态下的联合仿真研究，以验证所设计自动驾驶仪的有效性和可行性。

1 BTT导弹数学模型的建立

考虑各通道间的相互耦合，并作如下简化和假设:①不考虑导弹的挠性，视其为刚体；②不考虑推力偏心的作用，假设发动机推力的方向与弹体纵轴重合，忽略重力影响；③仅考虑导弹的短周期运动，认为导弹速度变化缓慢，在所研究的弹道特征点上，导弹的质量（m），转动惯量（J），速度（v），大气参数等视为常数；④导弹的攻角和侧滑角均为小量，即sin α≈α，cos α≈1，sin β≈β，cos β≈1，忽略二阶小量，即α2≈β2≈αβ≈0；⑤忽略舵机的非线性，用3个等效的一阶惯性环节代替实际舵机。

以某型BTT导弹为研究对象，基于以上假设，得到耦合状态下的数学模型如式（1）所示:

式（1）中:a1、a2、a3、a4、a5、b1、b2、b3、b4、b5、c1、c3为弹体的动力学系数，Jx、Jy、Jz为弹体的转动惯量；δxc、δyc、δzc为舵偏角指令，δx、δy、δz为实际舵偏角；为舵机的时间常数。

2 状态反馈H∞控制自动驾驶仪设计

由式（1）可知，BTT导弹数学模型存在耦合并且是非线性的，不便于控制器的设计和研究，需要进行解耦和线性化处理。把通道之间的耦合作用看作是有界干扰，同时在飞行导弹的弹道特征点上对导弹模型进行线性化，分别得到适合于状态反馈H∞控制器设计的各通道状态方程。由此所建立的三通道数学模型不同于直接忽略通道间的耦合得到的数学模型，其更接近于实际。

在实际中，攻角α和侧滑角β难以测量，所以BTT导弹自动驾驶仪设计时，一般采用法向过载ny和侧向过载nz作为状态变量，同时，为了使滚转角γ跟踪指令信号γc，故重新定义了两个误差er，eny作为滚转和俯仰通道中的一个新的状态变量，具体设计过程如下。

①滚转通道:选取变量er=rc-γ，r˙c=0，e˙r=-wx，结合导弹数学模型式（1），得到以x=［er，wx，δx］T为状态变量，控制输入u=δxc，干扰输入w=wywz的滚转通道数学模型如式（2）所示:

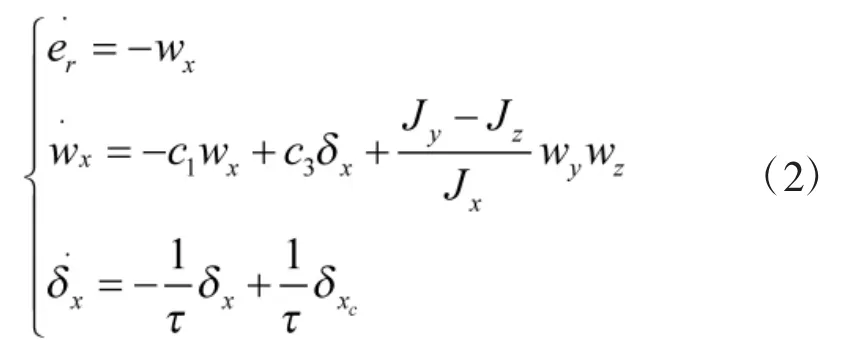
状态方程形式为:

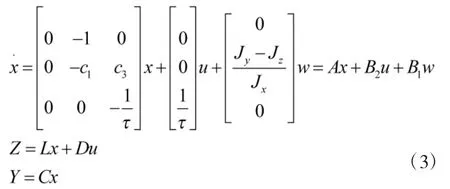
设计静态状态反馈控制器u=kx使得相应的闭环系统（3）是渐进稳定的:

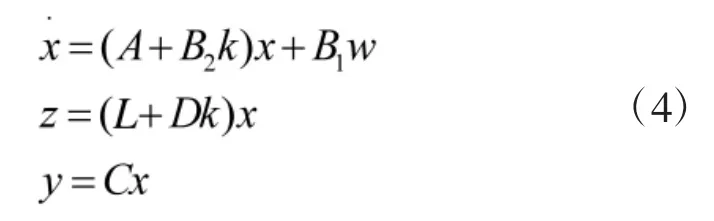
定理［11］:对于系统（4），存在一个状态反馈H∞控制器，当且仅当存在一个对称正定矩阵X和W，使得式（5）的矩阵不等式:

成立，进而，如果矩阵不等式（5）存在一个可行解X和W，那么u=W*X-1x是系统（4）的一个状态反馈H∞控制器。

代入某型BTT导弹滚转通道特征点的参数可得:

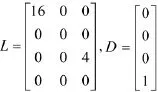
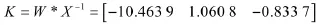
②俯仰通道:选取变量eny=nyc-ny，结合导弹数学模型式（1），得到以x=［eny，wz，δz，nyc］T为状态变量，控制输入u=δzc，干扰输入w=［wxβ，wxwy］T的俯仰通道数学模型为:x˙=Ax+B2u+B1w，其中，

代入BTT导弹特征点参数的具体参数值，利用MATLAB软件包求解线性矩阵不等式（5），求得可行解X和W，进而状态反馈H∞控制器为:

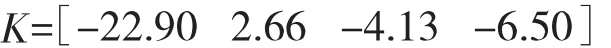
③偏航通道:结合导弹数学模型式（1），得到以x=［nz，wy，δy］T为状态变量，控制输入u=δyc，干扰输入w=［wxα，wxwz］T的偏航通道数学模型为:x˙=Ax+B2u+ B1w，其中，

代入BTT导弹特征点参数的具体值，利用MATLAB软件包求解线性矩阵不等式（5），可得可行解X和W，进而得到状态反馈H∞控制器为:

3 BTT三通道simulink联合仿真

BTT三通道联合仿真的期望目标是:滚转通道的滚转角γ能跟踪滚转角指令信号γc，俯仰通道的输出法向过载ny能尽快的跟踪给定的过载指令信号，同时偏航通道的输出侧滑角β和输出侧向过载nz尽可能保持为零。为了在工程上更具有实际意义，要求δmax≤45°，引入舵机模型，把三通道间的耦合作用作为干扰，根据前述所设计的自动驾驶仪搭建三通道联合仿真模型如图1所示。

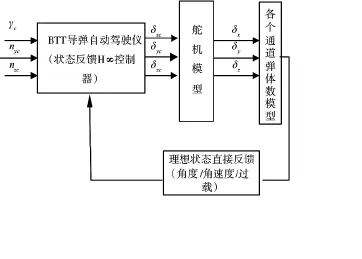
图1 BTT导弹三通道联合仿真框图

4 仿真研究与分析

根据所搭建的三通道BTT导弹自动驾驶仪仿真模型，在全耦合的状态下，进行三通道联合仿真。在滚转通道、俯仰通道分别加阶跃信号，幅值都为1，偏航通道指令nzc=0，滚转通道阶跃响应如图2所示，攻角、侧滑角响应如图3所示，滚转角速度、俯仰角速度、偏航角速度响应如图4所示，俯仰过载、偏航过载响应如图5所示。

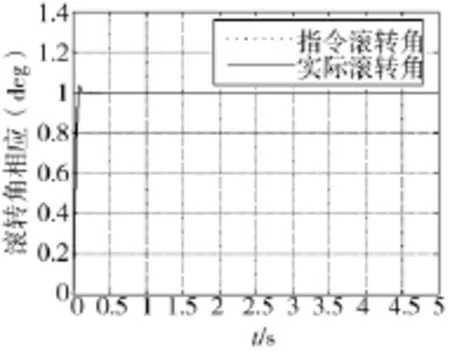
图2 滚转角响应曲线

从图2中可看出，实际滚转角指令可以快速跟踪指令滚转角，超调量小于3%，动态性能良好，最终能够实现无误差跟踪。

图3 攻角/侧滑角响应曲线

从图3中可看出，攻角响应经过1 s左右达到稳定并维持在1.8°左右，侧滑角最终趋于0°，满足BTT导弹|β|＜3°的控制要求。

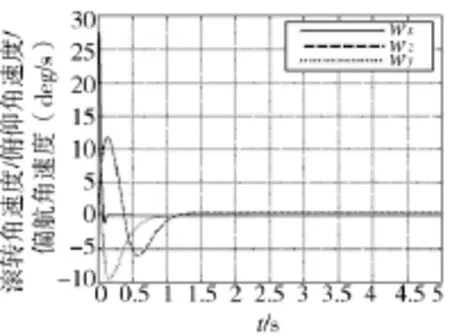
图4 滚转角速度/俯仰角速度/偏航角速度响应

从图4中可看出，滚转角速度、俯仰角速度、偏航角速度响应速度快，最终趋向稳定，满足BTT导弹三通道自动驾驶仪设计要求。

从图5中可看出，俯仰通道实际过载指令可以实现对过载指令信号的无误差跟踪。偏航通道的过载响应最终趋向于0，满足BTT导弹三通道自动驾驶仪设计要求。

5 结论

图5 俯仰过载/偏航过载响应曲线

以某型BTT导弹为研究对象，在考虑耦合的情况下得到更接近实际的导弹数学模型。在此基础上把通道之间的耦合作用看作是有界干扰，同时在飞行导弹的弹道特征点上，采用“小扰动”线性化方法将导弹模型进行线性化，分别得到适合于状态反馈H∞控制器设计的各通道状态方程。对三通道分别设计基于线性矩阵不等式的状态反馈H∞控制自动驾驶仪。根据所设计的自动驾驶仪，引入舵机模型，搭建BTT导弹三通道全耦合状态下的仿真模型，进行三通道联合仿真研究，结果表明所设计的状态反馈H∞控制自动驾驶仪能够实现对导弹制导指令的有效跟踪，满足BTT导弹的控制要求。

［1］童春霞，王正杰.双滑模变结构控制的BTT导弹自动驾驶仪设计研究［J］.系统仿真学报，2005，17（3）:518-521.

［2］王凌艳，吕鸣.BTT导弹的解耦问题综述［J］.飞航导弹，2009，6（2）:60-64.

［3］董翔宇，任利，刘云飞，等.BTT导弹变结构自适应控制仿真研究［J］.计算机仿真，2009，26（11）:65-68.

［4］张友安，杨旭，崔平远，等.BTT导弹的神经网络的自适应反馈线性化控制［J］.航空学报，2002，21（1）:84-86.

［5］林德福，孙彩英.H∞理论在BTT导弹自动驾仪设计中的应用［J］.系统仿真学报，2010，22（4）:991-995.

［6］王垒，王瑞革.基于H∞和μ综合的防空导弹鲁棒控制器设计［J］.舰船电子工程，2013，224（2）:38-40.

［7］赵红超，范绍里，徐君明.弹道导弹的自适应模糊滑模控制研究［J］.航天控制，2009，27（1）:49-52.

［8］ZHENG W G.An adaptive fuzzy variable structure controller for bank-to-turn missile［J］.Journal of Computional Information System，2011，7（2）:562-569.

［9］LIN C K.Mixed H2/H∞autopilot design of bank-to turn missiles using fuzzy basis function networks［J］.Fuzzy Sets and Systems，2007（158）:2268-2287.

［10］林建林，郑鲲鹏.导弹纵向自动驾驶仪线性二次型控制器设计［J］.四川兵工学报，2014，35（6）:19-21.

［11］郭艳艳，陈澜，张婧.无人机混合PID/H∞鲁棒着陆控制器［J］.火力与指挥控制，2011，36（7）:107-110.

［12］俞立.线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002.

Design of Autopilot of State Feedback H∞for BTT Missile

QU Xiu-min，LIU Shan-zhong，LIU Yong-bin
（Information Engineering College，Henan University of Science and Technology，Luoyang 471023，China）

In order to solve the problem of anti-jamming and robustness of bluetail ticket tracker（BTT）missile，considering coupling missile mathematical model is built，which makes it closer to the actual missile mathematical model.The coupling among the channels are used as interference and the missile model is made decoupled and linearized in the ballistic characteristics of the missile model.So that missile mathematical model of each channel is obtained.State feedback H∞controller is designed based on linear matrix inequality（LMI）.A full coupling of the three-channel simulation model is built，and then combined with simulation studies.The simulation results show that the design of the state feedback H∞control can achieve tracking of the missile guidance command effectively and meet the requirements of the BTT missile control.

bluetail ticket tracker missile，state feedback H∞control，linear matrix inequality，autopilot

V249.1；TJ765.3

A

1002-0640（2017）04-0142-04

2016-03-13

2016-04-06

国家自然科学基金（61203047）；河南省教育厅自然科学研究基金资助项目（12A120004）

屈秀敏（1990-），女，河南新乡人，硕士。研究方向：导弹控制算法。