基于对策论的舰载反潜机反潜作战兵力部署研究*

邓歌明，周晓光，冯百胜，刘洋

（1.海军航空兵学院，辽宁葫芦岛125001；2.解放军93357部队，辽宁鞍山114225）

基于对策论的舰载反潜机反潜作战兵力部署研究*

邓歌明1，周晓光1，冯百胜1，刘洋2

（1.海军航空兵学院，辽宁葫芦岛125001；2.解放军93357部队，辽宁鞍山114225）

为提高舰载反潜机反潜作战兵力部署的科学性，提升舰载反潜机反潜作战规划的能力，提出了一种基于对策论的舰载反潜机反潜作战兵力部署方法。首先推导了反潜机搜索条件下的潜艇生存概率模型，在此基础上，考虑潜艇打击能力、进攻目标价值等因素，构建了舰载反潜机反潜作战兵力部署maxminmax模型，给出了舰载反潜机反潜作战兵力部署maxminmax模型的求解算法，最后应用典型案例验证了模型的可行性和有效性。研究成果可为舰载反潜机反潜作战提供量化参考和实践依据。

舰载反潜机，反潜作战，兵力部署

0 引言

航母编队集多种反潜兵力、武器于一身，通过立体、大纵深、多方位对潜预警和侦察网络的侦察保障，在信息化指挥控制系统的指挥控制下以各种方式实施反潜作战。航母反潜多层防御体系如下页图1所示［1-2］。航母编队反潜作战力量通常包括反潜机、攻击型核潜艇、反潜直升机和水面作战舰艇等，分布在外、中、内反潜监视区内，构成纵深、立体、多层次的反潜防护体系。

舰载反潜机以航空母舰为基地，随航空母舰执行机动反潜任务，包括对潜艇实行搜索、监视、定位和攻击。舰载反潜机是航母编队最为重要的反潜作战力量，主要承担远程和中程的反潜作战任务，由于航母编队反潜作战力量数量有限，如何针对敌情，有效部署舰载反潜机作战力量，提高反潜作战效能是一个值得深入研究的课题。

外军在舰载反潜机反潜作战方面作了大量的研究工作，设计了多款反潜作战决策辅助训练系统［3-4］。国内在舰载反潜机反潜作战方面的研究刚刚起步，取得了一定的研究成果［5-9］。本文在前人研究的基础上对舰载反潜机反潜作战兵力部署问题进行了建模研究，提出了舰载反潜机反潜作战兵力部署优化模型，研究结果可为舰载反潜机反潜作战兵力部署提供方法和手段。

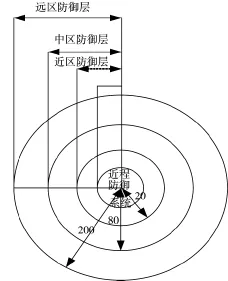
图1 航母编队反潜多层防御体系

1 舰载反潜机反潜作战兵力部署模型

1.1 潜艇生存概率

首先，推导y架反潜飞机在某一海域对一艘潜艇进行搜索攻击条件下，潜艇的生存概率。假定巡逻海域的面积为A。反潜飞机没有获取潜艇的位置的先验概率信息，因此，采取随机搜索策略。一旦潜艇被飞机搜索探测到，假定潜艇就被反潜飞机摧毁。因为潜艇相对于反潜飞机的速度较小，因此，可以假定在时间段Δt内，潜艇位置不变，那么y架反潜飞机在时间段Δt内对潜艇的探测概率为SyΔt/A，其中S为一架反潜飞机在单位时间内的搜扫面积。假定p（t）为到t时刻潜艇仍生存的概率，那么:

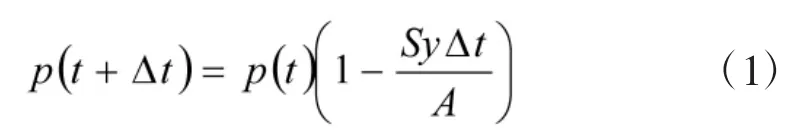
或者

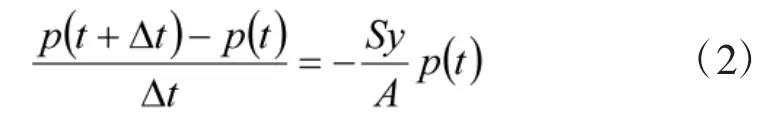
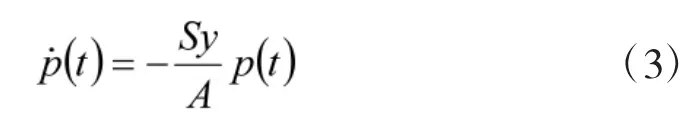
1.2 反潜作战兵力部署maxmin模型

为构建模型，定义符号如下:N为巡逻区域数量；X为潜艇数量；Y为舰载反潜机数量；Ai为在巡逻区域i内潜艇的不确定区域；Ti为在巡逻区域内舰载反潜机反潜时间；wi为在巡逻区域i内每艘潜艇所携带的武器数量；xi为巡逻区域i内潜艇部署的数量；yi为巡逻区域i内舰载反潜机部署的数量。

那么生存的潜艇所携带武器数量的期望为:

因此，最优的潜艇部署分布x*应该满足:

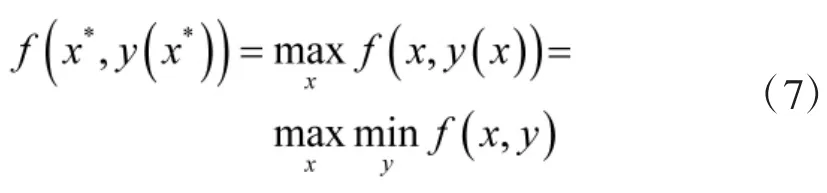
模型的完整形式如下:

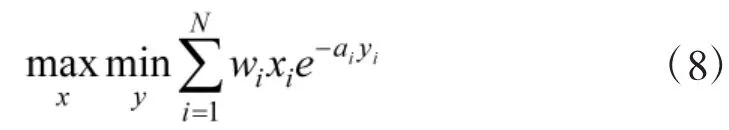
约束条件为:

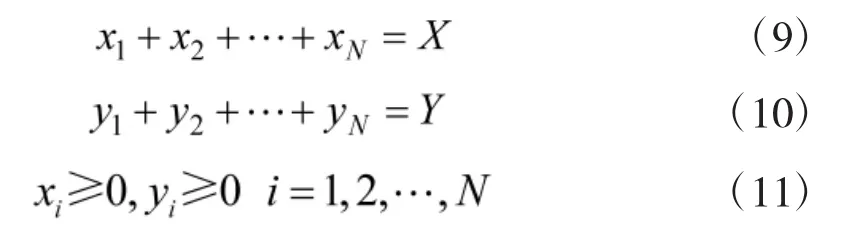
约束条件式（9）为进攻潜艇数量约束；约束条件式（10）为舰载反潜机数量约束；约束条件式（11）确保解为非负值，消除无意义的解。

上述构建模型中，没有考虑生存潜艇所载武器对航母群目标的摧毁打击问题。因为仅考虑潜艇的生存问题，为最大化潜艇的生存数量，将出现将潜艇放置在远离进攻目标位置的情况，以便最小化舰载反潜机对潜艇的摧毁数量，这与潜艇的进攻目标是相矛盾的。为解决这个问题，将目标价值引入目标函数，衡量潜艇对目标的摧毁数量和价值。

假定航母编队群由M地理单位格组成，在地理单位格内存在一个价值Vj的目标，如果栅格单位格内不存在目标，那么Vj=0。假定潜艇从区域i进攻单元格j内的目标毁伤概率为pij。区域i内潜艇对地理单位格j内目标进行攻击描述为zij。maxminmax优化模型为:

其中，约束条件式（16）是对每艘进攻潜艇打击次数的限制。约束条件式（17）是对潜艇对栅格内目标第一次攻击的武器数量的限制。

2 求解算法

在maxmin模型中，假定局中人X选择的策略为x0，那么针对局中人X的选择结果，局中人Y的最优选择策略y1可由下式确定:

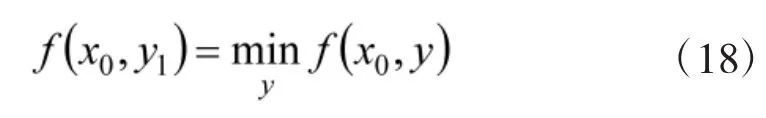
针对局中人Y的最优选择策略y1，局中X的最优选择策略x1可由下式确定:

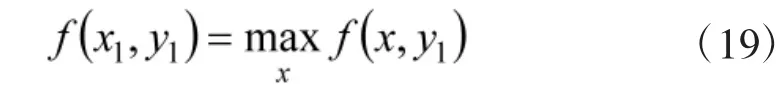
针对局中人Y相应的可以继续确定最优策略y2。针对局中人Y的策略y1和y2，局中人X的的最优策略x2可以由下式确定:

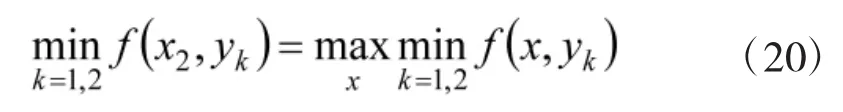
局中人交替采用同样的方式，那么xn和yn应该满足如下公式:

并且

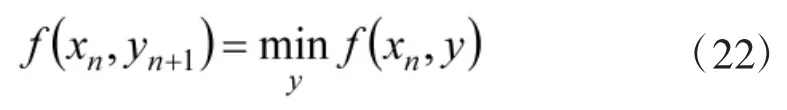
如果x*是的一个极值点，y*是相对于x*的反潜机反潜搜索的最优策略，那么（x*，y*）是一个鞍点解。

在求解局中人策略时，采用微分进化算法（DE）进行求解。DE算法被证明为最为有效的求解非线性规划的进化算法［10-12］。

用DE求解maxmin规划的算法流程如下:

Step 1:初始化种群规模NP（NP=10D），问题的维数D，缩放比例因子K，交叉概率CR，初始群体M，在定义域内随机初始化每一个个体。设置最大迭代次数T，置当前迭代计数器t=0，置最优值未变化计数器tt=0。用于表征问题解，

Step 2:计算每个个体的适应度fitness，求出最优适应度bestfitness及最优个体xgbest；

Step 3:若bestfitness变大，则tt=0，否则tt=tt+1；

Step 4:在种群中随机选择3个与xti不同的个体，按式（23）进行变异操作，生成变异个体

其中，rand（j）为［0，1］之间的均匀分布随机数，CR为范围在［0，1］之间的交叉概率；rnbr（i）为{1，2，…，D}之间的随机量。

其中，f为目标函数。

Step5:t=t+1，若tt＜M且t＜Iter，返回Step2，否则转入Step6；

Step6:优化结束。

3 典型案例分析

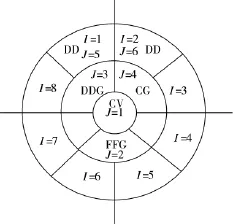
图2 舰载反潜机反潜作战想定

某典型舰载机反潜作战想定如图2所示。航母编队由1艘航母（CV），1艘导弹护卫舰（FFG），1艘导弹驱逐舰（DDG），1艘导弹巡洋舰（CG），2艘驱逐舰（DD）组成。

根据航母编队配置位置关系，划分为J=6个区域，对每个区域内编队组成进行标注价值如表1所示。

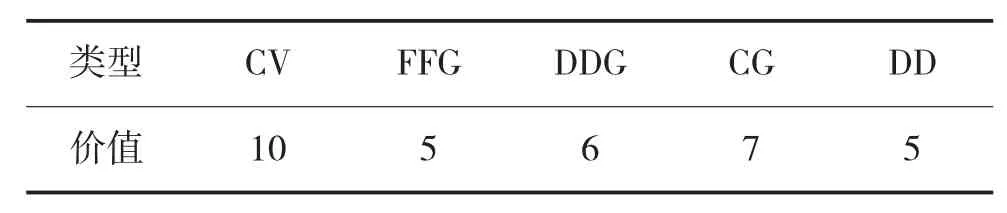
表1 航母编队目标价值

假定进攻潜艇采取中远程进攻策略，可进攻部署区域如下页图2所示区域:I=1，…，8。潜艇在区域I=1，…，8内对J=1，…，6区域内航母编队目标打击摧毁的概率如下页表2所示。

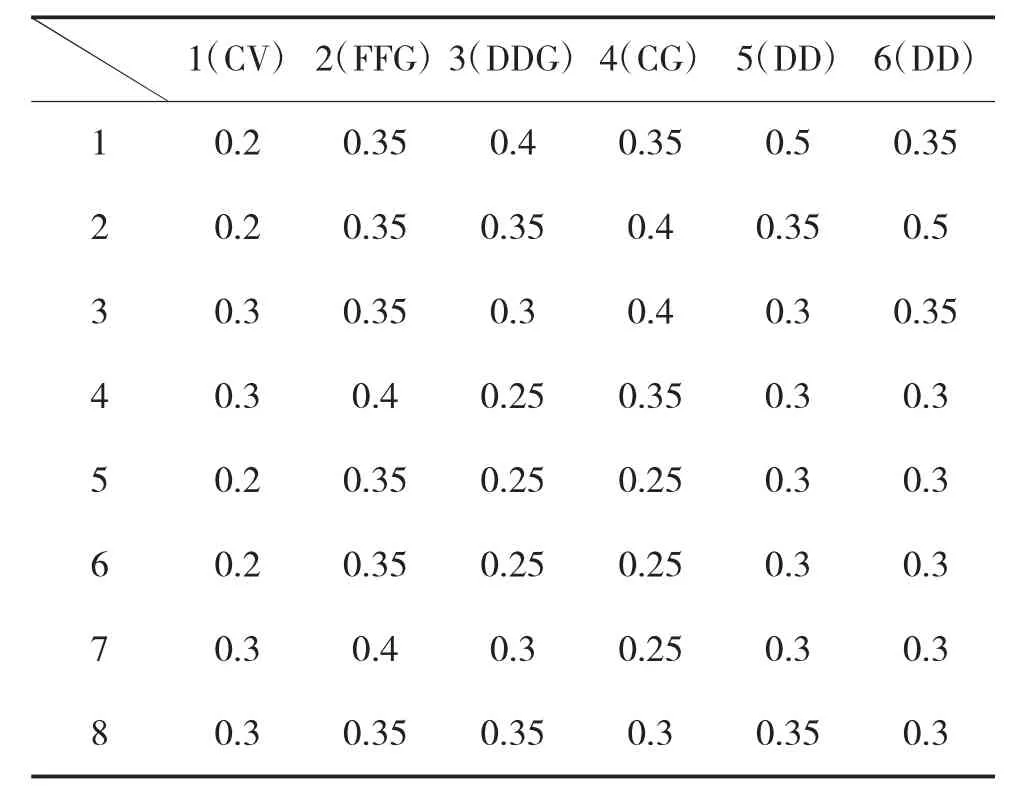
表2 各区域潜艇对区域内目标摧毁概率

假定进攻潜艇的数量为3，携带进攻武器数量为1。舰载反潜机的数量为3，根据作战想定可以假定舰载反潜机巡逻区域为1 000 km*km，舰载反潜机反潜时间为3 h。

根据上述假设，采用本文提出的基于DE的求解算法求解模型式（12），可以求得双方的最优部署策略和潜艇的进攻策略如下:

即潜艇应部署在区域，其中区域4，7，8内的潜艇选择一次打击，打击目标均为价值为10的航母。相对应的舰载反潜机的部署区域也为4，7，8。

4 结论

针对航母舰载反潜机反潜作战需求，本文提出了一种基于对策论的舰载反潜机反潜作战规划方法，并应用典型仿真案例验证了模型的有效性和可行性。研究结果显示，合理部署舰载反潜机可以有效提高舰载反潜机反潜作战效能。下一步的研究工作是舰载反潜机与航母其他反潜作战力量的协同作战问题。

［1］ADAM J.Tri-level optimization for anti-submarine warfare mission planning［D］.USA，California，Naval Postgraduate School，2008.

［2］SCOTT D.Game theoretic anti-submarine warefare mission planner［D］.USA，California，Naval Postgraduate School，2009.

［3］BROWN S.Optimal Search for a moving target in discrete time andspace［J］.OperationsResearch，1980，28（6）: 1275-1289.

［4］周晓光.舰载机作战运筹分析［M］.北京:国防大学出版社，2015.

［5］严必虎.透视航母战斗群反潜作战［J］.航母运用，2013（2）:47-53.

［6］屈也频.舰载固定翼反潜飞机的发展历程与启示［J］.论证与研究，2014，3（2）:9-13.

［7］陆铭华.基于多Agent仿真的编队协同反潜作战效能分析方法研究［J］.系统仿真学报，2011，23（3）:446-450.

［8］冯申，袁彩锦.航母战斗群与潜艇群对抗的建模分析［C］//西安军事运筹学年会，2013:335-338.

［9］顾建良.潜艇编队攻击航空母舰编队作战能力计算概述［J］.海军装备，1994，13（2）:22-26.

［10］阳明盛，罗长童.最优化原理、方法及其求解软件［M］.北京:科学出版社，2006.

［11］周晓光.基于预定作业周期的航母作战部署调度研究［J］.火力与指挥控制，2016，41（8）:70-74.

［12］吴亮红，王耀南，周少武.采用非固定多段映射罚函数的非线性约束优化差分进化算法［J］.系统工程理论与实践，2007，11（3）:128-133.

Research of Troop Disposition of Carrier-based Anti-submarine Airplane Based on Game Theory

DENG Ge-ming1，ZHOU Xiao-guang1，FENG Bai-sheng1，LIU Yang2
（1.Naval Aviation Institute，Huludao 125001，China；2.Unit 93357 of PLA，Anshan 114225，China）

In order to improve scientific decision and ability of operational planning of carrierbased anti-submarine airplane，the paper present a method of troop disposition of carrier-based antisubmarine airplane based on game theory.Firstly，the survival probability of a single submarine which comes under attact by anti-submarine airplane is deduced.Taking into account of attack abability of submaine and target value，the maxminmax troop disposition model is given.The Solving algorithm is given.Finally，experimental results demonstrate the feasibility and effectivity of the model for troop disposition.The research results can provide quantitative inference and operational evidence for troop disposition of carrier-based anti-submarine airplane.

carrier-based anti-submarine airplane，anti-submarine warefare，troop disposition

E925.4

A

1002-0640（2017）04-0063-04

2016-03-05

2016-04-07

国家社科基金（军事学）资助项目（14J003-XXX）

邓歌明（1972-），男，辽宁葫芦岛人，副教授。研究方向：航空反潜。