基于粒子群优化算法和烟花算法的图像配准
2017-05-02曹源武艳超
曹源+武艳超
【摘要】 本文以互信息作为相似性测度,提出改进的粒子群算法与烟花算法结合的混合算法来进行图像配准,该方法中粒子群的惯性权重动态变化提高粒子的搜索范围,并利用烟花算法的高斯变异算子增加粒子的多样性,防止粒子群算法陷入局部极值,并提高了配准的精确度,实验证明该方法在图像配准中取得不错的效果。
【关键词】 图像配准 互信息 粒子群优化算法 烟花算法
引言
图像配准是图像处理应用方面的一个基本问题,主要目的是将不同传感器、不同角度、不同时间或不同拍摄条件下获取的同一场景的两幅或者多幅图像进行对准、叠加(主要是几何意义上的),在很多领域有着广泛的应用,如计算机视觉、医学诊断与辅助治疗、遥感影像、三维建模、图像拼接等。通常情况下图像配准过程可分为3部分,首先确定参考图像和配准图像的变换方式,其次确定图像配准的相似性测度方式即相似性测度函数,最后确定对图像配准参数求解的优化算法。现有的图像配准方法主要分为基于特征的图像配准和基于灰度的图像配准。前者虽然计算简单且算法效率高,但是特征点的选取对配准精度和配准结果的影响很大,且特征点的正确选取较为困难。 而后者主要取决于图像的灰度统计特征,无需进行图像预处理且配准精度高,所以广泛应用于图像配准中。
一、标准的PSO算法
粒子群算法(PSO)是kennedy和Eberhart于1995年提出的一种基于群智能的随机优化算法。这类算法的仿生基点是:群集动物(如蚂蚁、鸟、鱼等)通过群聚而有效的觅食和逃避追捕。在这类群体的动物中,每个个体的行为是建立在群体行为的基础之上的,即在整个群体中信息是共享的,而且在个体之间存在着信息的交换与协作。粒子群算法就是以模拟鸟的群集智能为特征,以求解连续变量优化问题为背景的一种优化算法。
在粒子群算法,每个粒子代表所求解的优化问题中的一个可行解,它的适应度值由目标函数来确定,每个粒子都有自己的飞行速度,整个粒子群会共享最优解信息且跟随个体极值和全局极值进行移动,不断调整自己的位置和速度,直到最终发现最优解。

其中,pbesti(t)表示进化到t代时粒子i的个体最优位置;gbest(t)表示进化到第t代时整个粒子群的最优位置。
在公式(1)中粒子群算法的速度更新由三部分组成,第一部分成为粒子的先前速度,第二部分称为“认知(cognition)”部分,表明粒子个体的认知能力,来源于粒子自身的经验和思考,加速因子c1可以调节粒子飞向自身最好位置的飞行步长,第三部分称为粒子的“社会(social)”部分,表明粒子间的信息共享和相互作用,加速因子c2可以调节粒子向群体最优位置的飞行步长。
二、烟花算法
烟花算法通过模拟燃放的烟花在空中爆炸的这种行为建立相应的数学模型,通过引入随机因素和选择策略形成一种并行爆炸式搜索方式,进而发展成为能够求解复杂优化问题最优解的全局概率搜索方法。
烟花算法由四部分组成:爆炸算子、变异算子、映射策略、选择策略组成。
烟花算法具有局部搜索能力和全局搜索能力自调节机制。烟花算法中每个烟花的爆炸半径和爆炸火花数是不同的,适应度值差的烟花的爆炸半径较大,使其具有更大的“探索能力”———勘探性。适应度值好的烟花的爆炸半径较小,使其能够在该位置
周围具有更大的“挖掘能力”———开采性。此外,高斯变异火花的引入可以进一步增加种群的多样性。
三、互信息测度
互信息是信息理论汇总的一个基本概念,通常用于描述两个系统间的统计相关性,或者是一个系统中所包含的另一个系统信息的多少,它可以用熵来描述。互信息可用于图像配准的理论依据是:如果两幅图像已经配准,则它们的互信息达到极大值。

四、粒子群优化算法的改进
通过对标准粒子群算法的分析可以发现粒子群优化算法中存在如下问题:首先,参数控制范围太过笼统,针对不同的问题,如何选择合适的参数来达到最优化的效果。其次,粒子容易早熟,粒子的過早收敛会使函数陷入局部最优不能得到配准参数的全局最优值。本文对粒子群算法的改进思想是:首先将粒子群初始化,在进化过程中将根据粒子的收敛性动态调整惯性权重系数,因为当惯性权重w较小时,粒子群算法类似于局部搜索算法具有很强的局部开发能力;当惯性权重w较大时,粒子群算法类似于全局搜索算法,具有很强的全局搜索能力可以探索更广阔的搜索区域,但它的收敛速度更慢,根据以上情况我们可以动态调整粒子群的惯性权重,使得在粒子群飞行的前期,w值较大,在粒子群飞行的后期w值较小,公式如下: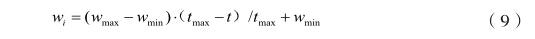
wi为当前粒子i的惯性权重,ai为粒子的适应度函数值,amax为粒子群当前最大适应度函数值,t为当前的跌倒次数,tmax为最大迭代次数;由于粒子群是从随机解出发寻找最优解,且存在早熟的可能不能保证每次均能找到最优解,此时我们需要定义一个粒子群适应度的理论最优值Fbest和适应度的标准差S,当S=0时,若全局适应度全局最优值gbest=Fbest,我们可知粒子得到全局最优解,若gbest
我们引入烟花算法中的高斯变异算子改变粒子的多样性,公式如下
xij=xij+(xbj-xij)·e (10)
其中,e为一个高斯分布的随机变量,其均值为0,方差为1;xbj为当前烟花种群中适应度最优的烟花在第j维上的位置信息。xij为当前烟花i在第j维上的位置信息。此时算法的具体步骤如下。
1、输入参考图像和配准图像,初始化粒子群的位置和速度。
2、根据公式(5)计算粒子的适应度。
3、根据公式(3)和(4)更新粒子的个体极值和全局极值。
4、根据公式(9),更新粒子的惯性权重w
5、根据公式(1)和(2)更新粒子的速度和位置。
6、判断终止。计算群体适应度标准差 S。并根据适应度理论最优值Fbest判断粒子群是否达到全局最优,若达到则终止;若未达到则进行下一步。
7、根据公式(10),更新粒子的位置。返回步骤(2)继续运行。
五、实验结果及分析
在本次算法的实验中,参考图像大小均为为256×256,分别使用标准粒子群优化算法,本文的混合优化算法和文献[5]算法進行处理。实验数据如表1;配准前后的3组图像如图1。
从表1中可以看出:由于粒子群初始解的随机性,标准的PSO算法和文献[5]的算法在图像配准中均会陷入局部极值,虽然这两种算法运算速度快,但是图像配准的精确度不够高,而且配准的平均误差比较大,本文中的算法虽然比其它两种算法相比耗时较长,但是该算法配准的精度高,对图像配准有不错的效果。
六、 结论
本文提出的基于互信息的PSO-FWA算法的图像配准方法,在配准过程中人工干预少,且只依赖图像的灰度统计信息,避免了图像预分割和特征提取等操作,大大提高了图像的配准效率。而且经过实验证明,该算法可极大的避免函数陷入局部最优值,保证了较高的配准精度,在图像配准方面有很好的效果,具有较好的实用性和实际应用价值。
参 考 文 献
[1] 张银蒲,基于互信息的图像配准技术的研究[J].核电子学与探测技术,2012,32(5):562-568
[2] 陈显毅,图像配准技术及其MATLAB 编程实现[M].北京: 电子工业出版社, 2009.
[3] 黄琨,多模态优化粒子群算法的研究[J].大众科技,2016,18(2):29-31
[4] 谭营,郑少秋,烟花算法研究进展[J].智能系统学报,2014,9(5):515-528
