基于当前统计模型的水下目标自适应跟踪算法

张晴月++蒋志迪

【摘 要】为实现水下机动目标的精确跟踪，提出了一种基于当前统计模型的水下目标自适应跟踪算法。该算法引入当前统计模型作为模型基础，并结合卡尔曼滤波算法，通过自适应调整滤波增益，对目标当前状态进行实时估计，较为准确地反映水下目标实际机动特性，解决了传统卡尔曼滤波算法不能有效跟踪水下目标转弯、变速等复杂机动情况的问题。仿真结果表明，在6000 m×5000 m×3000 m的水下三维空间内，算法跟踪效果较好，有效实现了对水下机动目标的精确跟踪。

【关键词】水下目标跟踪 当前统计模型 卡尔曼滤波 自适应跟踪法

1 引言

近年来，陆地资源逐渐被开采殆尽，海洋资源的勘测与开发便越来越受到世界各国重视，水下目标跟踪技术也因此得到不断发展，对其精度的要求变得越来越高。

在复杂的水下环境中，目标运动存在转弯、加速等多种复杂机动的可能。建立机动目标运动模型是对目标进行跟踪的基础[1]。目前，描述目标机动运动的模型主要有Jerk模型、交互多模型、当前统计模型等[2]。其中，Jerk模型在目标机动性较高的情况下具有良好的跟踪效果，但在处理阶跃机动时存在确定性误差，性能有所限制。交互多模型利用多个运动模型交互进行加权估计，适合于多运动状态跟踪的处理，但受模型集影响，性能较依赖于单个模型，易出现模型偏差问题[3]。当前统计模型作为非零均值时间相关模型，具有加速度自适应特性，能较准确地估计机动目标当前状态，机动实时适应能力较强，并有良好的鲁棒性，受到广泛应用[4]。

水下跟踪定位系统中，所测角度、距离等目标信息的处理占据重要环节[5]。为保证跟踪技术得到有效实现，需要有性能较优的滤波算法来进行滤波处理，完成对目标的状态估计和预测。常用的滤波跟踪算法有α-β滤波、粒子滤波和卡尔曼滤波等。α-β滤波形式简单，易于工程实现，但滤波性能受所选参数限制，精度不高。粒子滤波能有效处理非线性非高斯情况，但计算量较大，运算相对复杂[6]。卡尔曼滤波对于线性高斯问题能达到较为理想的处理效果，但当水下目标处于转弯等多种机动状态时，并不能很好地调整参数以适应目标状态，从而导致收敛速度变慢，跟踪精度下降[7]。

为了提高水下机动目标跟踪的精确性，本文将当前统计模型与卡尔曼滤波算法相结合，提出基于当前统计模型的水下目标自适应卡尔曼跟踪算法（ACS-KF，Adaptive Current Statistical model-Kalman Filter algorithm），利用当前统计模型的自适应特性，实时调整卡尔曼滤波算法中滤波增益，以适应水下目标运动状态的不断变化，有效地实现对水下目标转弯、加速等多种复杂机动情况的精确跟踪，提高跟踪精度。

本文首先介绍水下目标跟踪背景，提出ACS-KF自适应跟踪算法，接着阐述算法原理，并将其应用于三维水下目标跟踪，最后通过仿真对该算法的性能进行验证。

2 基于当前统计模型的水下目标自适应

跟踪算法

2.1 当前统计模型

目标在复杂的水下环境中可能会出现多种机动状态，如果采用零均值加速度模型来描述，易出现与实际状态不符的情况，导致跟踪出现较大偏差。本文采用的目标运动模型为当前统计模型，其本质上属于非零均值时间相关模型，采用修正的瑞利分布描述加速度的概率密度，其均值为当前加速度预测值，并假定机动目标在以当前加速度进行机动时，下一时刻的加速度范围有限，且在当前加速度的邻域内。根据当前统计模型的假设，目标加速度满足式（1）、式（2）：

3 实验仿真与分析

在水下三维空间中布置声呐基阵，测量基阵到运动目标的方位角、距离、多普勒频移以及径向速度等观测值，再利用相应定位算法进行解算，最终确定目标的测量方位。实际水下环境较为复杂，经定位算法解算后，水声基阵获得的目标三维坐标信息含有测量噪声等干扰。现模拟水下基阵对水下目标进行定位环境跟踪，假定探测器沿三坐标轴方向独立地检测目标运动，获得目标三维坐标测量值。实际系统测量值为目标真实值与测量噪声的叠加，仿真对应真实轨迹与零均值、方差为30的高斯白噪声叠加。

水下目标通常在距离水面一定深度的地方运动，可能出现匀速、变速和转弯等多種机动状态。仿真中，目标在水下三维空间的运动轨迹包含匀速直线、匀加/减速，慢、快转弯等多种可能的运动情况，具有代表性。根据目标水下实际机动特性，当前统计模型机动频率β为0.1，加速度范围为[-0.2 m/s2， 0.2 m/s2]。蒙特卡罗仿真100次，通过对KF算法和ACS-KF算法进行比较，验证算法跟踪性能。

目标模拟机动过程如下：扫描3200次，扫描周期为0.25 s，其中：在0 s—200 s、300 s—500 s，目标作匀速直线运动；在200 s—300 s、500 s—600 s、600 s—800 s，目标分别作了三个转弯，机动强度逐渐增大。在200 s—300 s段，目标沿X轴方向以加速度0.05 m/s2作匀加速运动，Y轴方向以加速度0.02 m/s2作匀加速运动，Z轴保持速度0 m/s；500 s—600 s段，X轴上保持0 m/s，Y轴上以加速度-0.15 m/s2作匀加速运动，Z轴方向开始以加速度0.15 m/s2作匀加速运动，运动到D处；600 s—800 s段，Y轴方向加速度变为-0.02 m/s2，Z轴方向以10 m/s匀速运动，直至运动结束。目标初始位置为O点，坐标（x0， y0， z0）为（6000 m， 1000 m， 0 m），初始速度（vx0， vy0， vz0）为（8 m/s， 5 m/s， -10 m/s）。

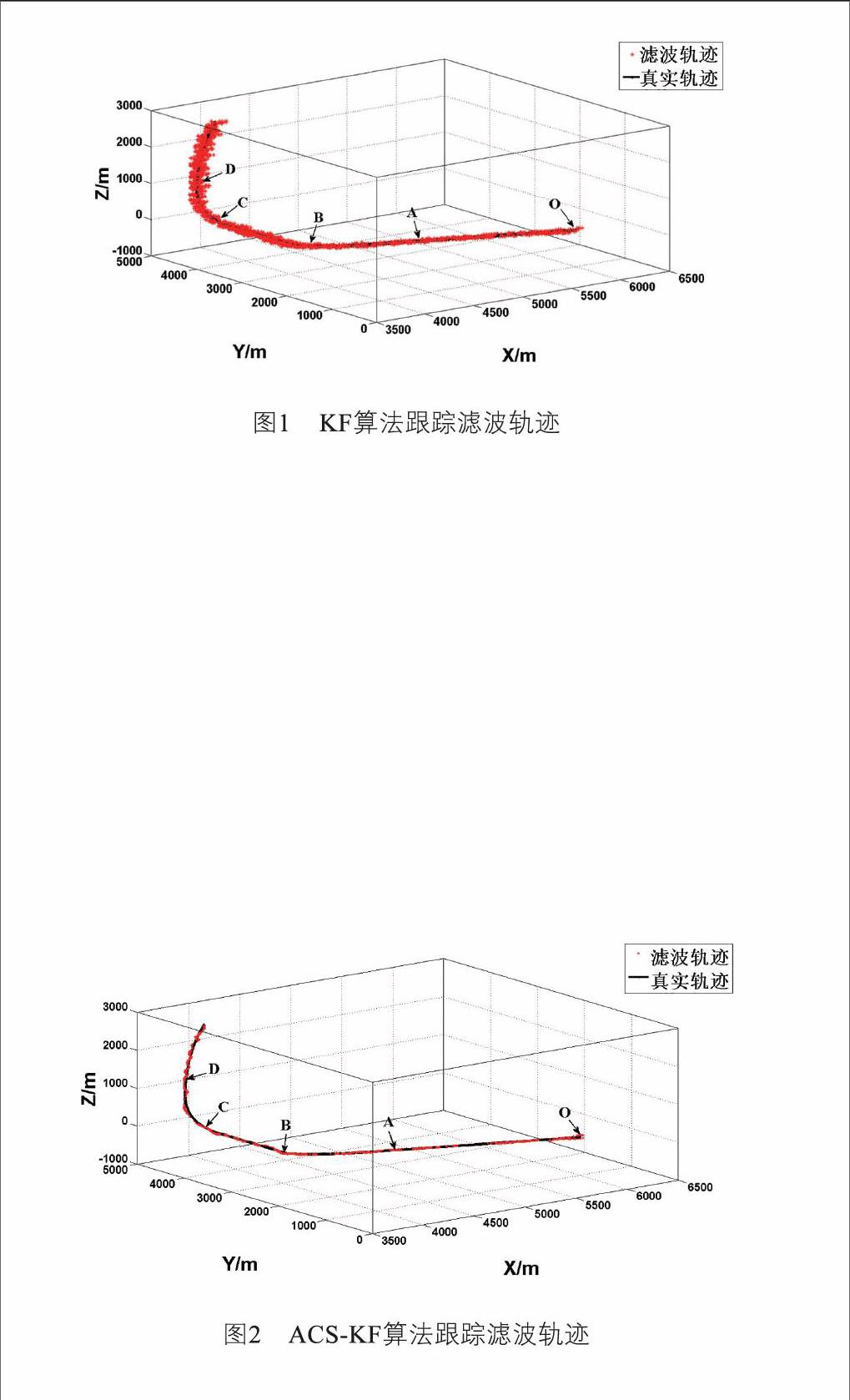
图1为采用KF滤波算法的目标滤波轨迹，可以看出，单独KF滤波处理后的轨迹以真实轨迹为中心有较大的波动，偏离较大。在初始OA段，目标作匀速直线运动，滤波后轨迹与真实轨迹较为接近，扰动较小。从A点开始作慢转弯运动，此时滤波轨迹与原轨迹开始出现明显偏离，在接下来的BC段进行匀加速直线运动，虽然较接近于真实轨迹，但仍存在波动。而后在C、D两处快转弯，明显出现较大偏差。整个运动过程中，目标滤波轨迹整体偏差偏大，各个方向上误差由最初几米增大到近一百米左右。

圖2为采用ACS-KF算法的目标滤波轨迹。可以看出，在A、B的慢转弯处，以及C、D的快转弯处，ACS-KF算法滤波轨迹在目标真实轨迹附近波动较小，与图1中KF算法滤波轨迹相比较，其滤波轨迹与真实轨迹较为接近，偏差较小。同时在其他非机动时间段基本保持与原KF算法同样良好的处理效果。由此看出，ACS-KF算法在实现目标机动与非机动情况的精确跟踪方面有较好的优势，跟踪精度较高。

图3和图4分别为KF算法和ACS-KF算法下目标机动加速度估计值与真实值曲线。图4中ACS-KF算法得到的加速度滤波估计值与真实值基本趋于一致，在各个方向轴加速度变化时间段，加速度滤波估计值在真实值附近仅小范围波动，而图3中加速度滤波估计曲线波动较大，同真实值存在较大偏差，跟踪效果较差。由此看出，ACS-KF算法能够自适应跟踪机动加速度的变化，及时反映目标机动特性，较单独KF算法有优势。

图5为KF算法下各坐标轴方向的误差标准差。测量间隔时间设为100 s，选取7个对应时刻坐标点进行分析。图中标注的数值为每一间隔点处测得的各方向轴误差均值标准差。可看出，100 s—700 s段产生的误差标准差取值基本处在0.4～0.6 m，维持在0.5 m左右产生小幅度波动。比较图6，ACS-KF算法下各方向轴的误差标准差取值范围在0.1～0.2 m，保持在较低水平，相比KF算法对应标准差值有显著减小，减小幅度为0.3～0.4 m左右，具备良好的跟踪效果。

综上所述，通过对两算法滤波轨迹、机动加速度自适应跟踪特性以及各坐标轴运动误差标准差值进行分析与比较，ACS-KF算法相对于传统KF算法滤波效果改进较为显著，对于水下机动目标的自适应跟踪能力较强，跟踪精度有明显提高。

4 结束语

本文提出的ACS-KF算法利用当前统计模型加速度方差自适应特性，通过实时调整滤波中过程噪声方差，进而自适应调整卡尔曼滤波增益，可提高跟踪精度。以水下基阵对水下目标跟踪定位为仿真背景，采用ACS-KF算法对目标进行跟踪。当目标出现变速、转弯等多种复杂机动情况时，ACS-KF算法通过自适应调整滤波参数，能够较准确地反映水下目标实际机动特性。仿真结果表明，所提出的ACS-KF算法得到的目标轨迹误差处于较低水平，滤波效果改进较为显著，有效提高了跟踪精度，实现了对水下目标更为精确的跟踪。

参考文献

[1] Jianfeng WU， Gang LI， Fuzhou MA. Research on Target Tracking Algorithm Using Improved Current Statistical Model[A]. Proceedings of IEEE International Conference on Electrical and Control Engineering （ICECE）[C]. 2011： 2515-2516.

[2] 侯俊林. 高机动目标Jerk模型跟踪算法研究[D]. 哈尔滨： 哈尔滨工程大学， 2013： 31-46.

[3] Blom H A P， Bar-Shalom Y. The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients[J]. IEEE Transactions on Automatic Control， 1998，33（8）： 780-783.

[4] Zhou Hongren， Jing Zhongliang， Wang Peide. Maneuver-ingTarget Tracking[M]. Beijing： National Defense Industry Press， 1991： 10-153.

[5] Maki T， Matsuda T， Sakamaki T， et al. Navigation Method for Underwater Vehicles Based on Mutual Acoustical Positioning With a Single Seafloor Station[J]. IEEE Journal of Oceanic Engineering， 2013，38（1）： 167-177.

[6] P H Foo， G W Ng. Combining the interacting multiple model method with particle filters for maneuvering target tracking[J]. IET Radar， Sonar and Navigation， 2011，5（3）： 234-235.

[7] 王康，蒋志迪，张晴月. 基于IMMKF-3D的水下目标跟踪算法[J]. 移动通信， 2016，40（16）： 73-79.

[8] 黄小平，王岩. 卡尔曼滤波原理及应用——MATLAB仿真[M]. 北京： 电子工业出版社， 2015： 1-4， 36-37.

[9] 杨艳成，张丽珂，郭永亮. 一种“当前统计”模型的模糊自适应算法[J]. 指挥控制与仿真， 2011，33（3）： 46-49.

[10] 钱华明，陈亮，满国晶，等. 基于当前统计模型的机动目标自适应跟踪算法[J]. 系统工程与电子技术， 2011，33（10）： 2154-2158.

[11] Yongjian Yang， Xiaoguang Fan， Shengda Wang， et al. A new parameters adaptively adjusting method of current statistical model[A]. Proceedings of the 2015 IEEE International Conference on Information and Automation[C]. 2015： 1738-1739.

[12] S Vasuhi， V Vaidehi， T Rincy. IMM Estimator for Maneuvering Target Tracking with Improved Current Statistical Model[A]. Proceedings of IEEE-International Conference on Recent Trends in Information Technology[C]. 2011： 286-290. ★