带有分支梁的导弹模态剪力和模态弯矩计算方法

王 乐，冷德新，蔡毅鹏

（中国运载火箭技术研究院，北京，100076）

带有分支梁的导弹模态剪力和模态弯矩计算方法

王 乐，冷德新，蔡毅鹏

（中国运载火箭技术研究院，北京，100076）

模态剪力和模态弯矩是导弹横向动态载荷计算及识别的重要基础，完善了带有分支梁的导弹模态剪力和模态弯矩计算方法。首先从剪力和弯矩的基本定义出发，推导了梁-质量块有限元模型主梁和分支梁模态剪力和模态弯矩计算方法，然后采用模态叠加方法计算横向静力作用下导弹的飞行载荷，并与静力学计算结果进行对比。结果表明，采用模态剪力叠加和模态弯矩叠加计算结果随着模态数量的增加逐渐逼近静力学计算结果，当考虑所有的模态时，计算结果与静力学计算结果完全相同，验证了模态剪力和模态弯矩计算方法的正确性。

主梁；分支梁；模态；模态剪力；模态弯矩

0 引 言

载荷设计是导弹总体设计的重要内容，其主要任务是根据作用于导弹的外力给出结构内部的剪力、弯矩和轴力等为结构设计和强度校核提供依据。载荷设计中的静力学方法是工程设计中广泛使用的方法[1]，研究外力作用周期较长情况下结构的内力。例如计算导弹横向飞行载荷时，首先根据作用于导弹上的外力计算导弹整体的平移和转动加速度，然后依据外力和惯性力平衡原理，用截面法得到各个截面的剪力和弯矩。文献[2]指出，静力理论忽略了结构本身的振动、变形性质，没有考虑结构的动力特性。在某些情况下，如计算潜射导弹出水过程中由空泡溃灭产生的横向冲击载荷时[3]，静力学方法是不适用的，必须根据结构的动力响应研究导弹的内力，模态叠加法是其中最重要的方法，该方法在出水过程横向载荷设计和飞行载荷识别中得到了广泛应用[2,4,5]。

采用模态叠加法计算横向载荷时，需要计算各阶模态的模态剪力和模态弯矩，然后将模态剪力和模态弯矩用相应的模态坐标进行线性叠加，就得到动态外力作用下真实的结构内力。梁-质量块有限元模型是工程设计中常用的动力学模型，在计算模态弯矩时，一些文献忽略了节点上转动惯量的影响[6～9]，此外，分支梁模态剪力和模态弯矩的计算方法还需进一步完善。

为此，本文从剪力和弯矩的基本定义出发，推导了梁-质量块有限元模型主梁和分支梁模态剪力和模态弯矩计算方法，考虑了节点转动惯量对模态弯矩的影响。为了检验本文计算方法的正确性，采用模态叠加方法计算了横向静力作用下导弹的飞行载荷，并与静力学计算结果进行对比。结果表明，采用模态剪力叠加和模态弯矩叠加计算结果随着模态数量的增加逐渐逼近静力学计算结果，当考虑所有的模态时，计算结果与静力学计算结果完全相同。本文带有分支梁的导弹模态剪力和模态弯矩计算方法对于飞行载荷识别、动载荷计算具有一定的参考价值。

1 主梁的模态剪力、模态弯矩计算方法

设主梁-质量块有限元模型一共有n个截面，每个截面上有一个线位移和角位移，并且有集中质量mi和转动惯量Ii，每个节点上作用的集中力和集中力矩分别为Fi和FMi，如图1所示。

图1中共有2n个自由度，由总质量矩阵M和总刚度矩阵K可得模型的频率和振型，共有2n阶模态，其中前两阶为刚体模态，对任意一阶振型和频率，有：

则：

式中φ为各阶振型组成的矩阵；根据模态叠加原理，位移可以分解为 =Xφq，则：

式（3）进一步可写为

式中为广义坐标。

由于本文讨论的是集中质量系统，则总质量矩阵M为对角矩阵，因此有：

1.1 模态剪力

如果不考虑阻尼力，导弹的运动方程为

式中F为各个节点外力所构成的列向量。本文采用材料力学中剪力和弯矩的符号定义，由力的平衡方程可得第j截面的剪力为

对于有2n个元素的列向量A，定义算子，使得：

则：

由式（4）可得：

由式（5）可得：

交换求和顺序可得：

则第j个截面的第i阶模态剪力为

1.2 模态弯矩

根据力矩平衡方程可得第j个截面的弯矩可写为

对于有2n个元素的列向量A，定义算子，使得：

定义2 2×nn的对角矩阵：

则，

由式（4）可得：

由式（5）可得：

交换求和顺序可得：

第j个截面的第i阶模态弯矩为

2 分支梁的模态剪力、模态弯矩计算方法

图2为有一端固支，另一端自由的分支梁。

按照主梁模态剪力和模态弯矩的计算方法可得分支梁各位置左截面的模态剪力和模态弯矩为

3 算 例

为了验证本文带有分支梁的导弹模态剪力和模态弯矩计算方法的正确性，将计算结果与静力学结果对比。现有某导弹作用在主梁上各节点的横向外力如图3所示。各节点无外力矩，分支梁无任何外力。

在静力学计算中不考虑导弹的初始位移和速度，各阶模态的广义坐标为

式中为第i阶模态的广义力；为第i阶模态的广义刚度。

以平面梁单元建立导弹有限元模型，主梁上有49个节点，分支梁有6个节点，主梁和分支梁共用1个节点，共有108个自由度，前两阶模态为刚体模态，导弹的前三阶弹性模态频率如表1所示，振型如图4所示。

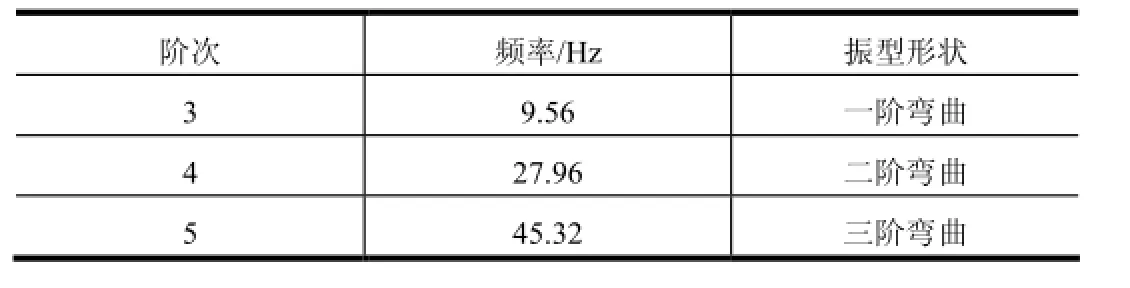
表1 前三阶弹性模态频率

按式（22）的方法计算弹体各阶模态的广义坐标，分别采用静力学方法和模态剪力叠加和模态弯矩叠加的方法计算飞行载荷。计算结果如图5～图12所示。

由图5～图12可知，当只考虑一阶弹性模态时，模态剪力叠加结果和模态弯矩叠加结果与静力学计算结果相比相差较大；随着模态数量的增加，计算结果逐渐逼近静力学计算结果；当考虑所有的模态时，计算结果与静力学结果完全相同。

当考虑所有的模态时，采用以上两种方法计算的分支梁载荷对比结果如表2所示。

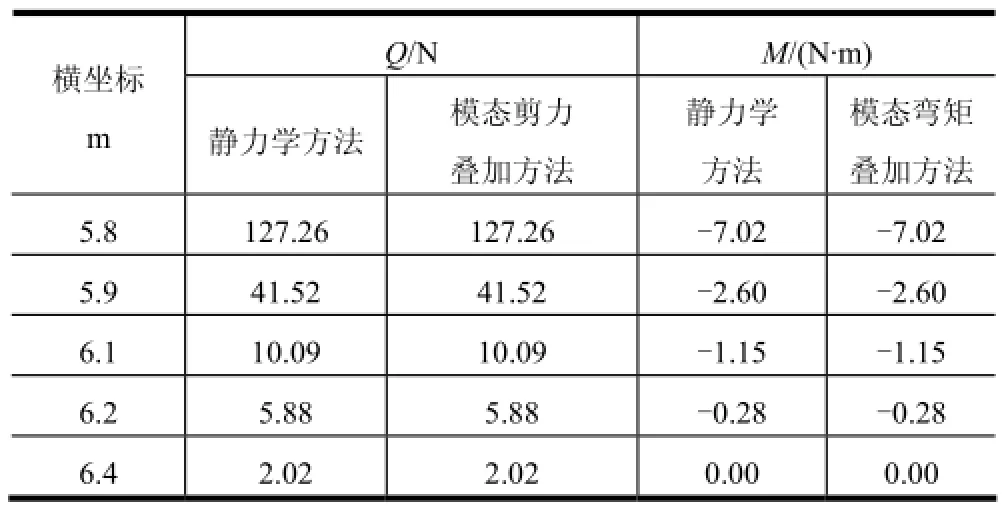
表2 分支梁载荷对比

由表2可知，采用两种方法计算的分支梁载荷结果完全一致。

4 结 论

本文从剪力和弯矩的基本定义出发，推导了带有分支梁导弹的模态剪力和模态弯矩计算方法，考虑了节点转动惯量对模态弯矩的影响，给出了主梁和分支梁模态剪力和模态弯矩的计算公式。为验证计算方法的正确性，采用模态叠加方法计算了横向静力作用下导弹的飞行载荷，并与静力学计算结果进行对比。结果表明，采用模态剪力叠加和模态弯矩叠加的计算结果随着模态数量的增加逐渐逼近静力学结果；当考虑所有的模态时，计算结果与静力学计算结果完全相同。

[1] 蒋鲁佳, 辛万青, 孟令涛, 戴婷婷, 庞宝强, 杨新龙. 导弹超声速飞行横向气动载荷估算系统[J]. 导弹与航天运载技术, 2010(5): 21-23.

[2] 尹云玉, 吕海波, 李宁, 陈敏. 潜射火箭出水过程横向响应载荷研究[J].导弹与航天运载技术, 2007(6): 12-16.

[3] 权晓波, 李岩, 魏海鹏, 吕海波, 辛万青, 鲁传敬. 航行体出水过程空泡溃灭特性研究[J]. 船舶力学, 2008, 12(4): 545-549.

[4] 尹云玉. 固体火箭自由运行状态截面弯矩识别方法[J]. 宇航学报, 2010, 31(7): 1706-1710.

[5] 尹云玉. 固体火箭横向响应载荷识别方法[J]. 宇航学报, 2009, 30(6): 2135-2139.

[6] 龙乐豪, 等. 总体设计(上册) [M]. 北京: 宇航出版社, 1989.

[7] 黄怀德, 等. 振动工程(下册) [M]. 北京: 宇航出版社, 1995.

[8] 吕海波, 权晓波, 尹云玉, 魏海鹏, 姚熊亮. 考虑水弹性影响的水下航行体结构动响应研究[J]. 力学学报, 2010, 42(3): 350-356.

[9] 陈智勇. 时变弹性梁横向响应载荷识别[J]. 导弹与航天运载技术, 2008(2): 49-52.

A Method of Obtaining Modal Shear Forces and Modal Bending Moments of the Missile with Branch Beam

Wang Le, Leng De-xin, Cai Yi-peng
(China Academy of Launch Vehicle Technology, Beijing, 100076)

Modal shear force and modal bending moment are the foundation of the calculation and identification of transverse dynamic load, the method of obtaining modal shear forces and modal bending moments of the missile with branch beam was improved. First, the modal shear forces and modal bending moments of the major beam and branch beam in the Beam-Mass finite element model were deduced from the definition of shear force and bending moment. Then, the flight loads of a missile under transverse static loads were calculated by mode superposition method, the results were compared to those of statics. It’s showed that the results of mode superposition method gradually approach those of statics with the numbers of modes, they are the same when all the modes are included, so the method of obtaining modal shear forces and modal bending moments is verified.

Major beam; Branch beam; Mode; Modal shear force; Modal bending moment

O327

A

1004-7182(2017)02-0020-05

10.7654/j.issn.1004-7182.20170205

2015-07-03；

2016-01-15

王 乐（1984-），男，高级工程师，主要研究方向为载荷与环境设计