沙地樟子松边材宽度与胸径关系研究

周凤艳

(辽宁省固沙造林研究所，辽宁 阜新 123000)

沙地樟子松边材宽度与胸径关系研究

周凤艳

(辽宁省固沙造林研究所，辽宁 阜新 123000)

对相同立地条件下的10、20、30、40年生樟子松人工固沙林进行胸径、边材厚度测定，分析不同年龄边材厚度与胸径相关关系及不同年龄边材生长特征。结果表明：10年生时平均边材宽度为6 cm；20～30年生平均边材增幅小；30～40年生时边材增幅大。10年、20年生樟子松边材厚度与胸径关系模型符合抛物线模型，拟合方程分别为y=0.146 2x2-1.554 6x+6.401 7 (R2=0.975 3)、y=-0.057 6x2+1.456 1x-4.761 9(R2=0.669 7)；30年生樟子松东、南两个方位边材厚度与胸径关系可用曲线拟合，东方位符合指数模型，方程为y= 0.980 1 e0.081 1x(R2=0.733 7)，南方位符合抛物线方程y=0.009x2-0.07x+1.940 4 (R2=0.518 7) 或指数方程y=1.082 7 e0.065 4x(R2=0.516 4)；40年生樟子松的东方位和北方位可用幂指数模型拟合，分别为y=0.196 5x1.077 2(R2=0.476 8)和y= 0.029 1x1.748 8(R2= 0.785 5)，南、西方位的相关关系可用指数模型拟合，表达式分别为y=0.673 e0.104 7x(R2=0.750 4)和y= 0.455 8 e0.123 84x(R2=0.934 6)。不同年龄边材宽度显著差异，可以反映其生长状况、水分利用对策、物质生产等方面的特征。

边材厚度；樟子松；胸径；沙地

边材向心材的转化过程是树木生长中的一个重要的生理学过程，树木叶量或叶面积与树干的边材面积呈正相关，边材面积与叶面积之比也常常用于表征树木的蒸腾耗水或固碳能力；心材和边材材性上的差异也会影响木材的加工和利用，因此研究树木边材和心材生长发育规律，是探索树木水分关系和碳代谢机理、构建树木生长收获模型、有效利用木材的基础[1]。

樟子松(Pinussylvestrisvar.mongolica)原产内蒙古红花尔基地区，20世纪50年代成功引种到辽宁省阜新市章古台沙地(科尔沁沙地的东南部)。与中国主要森林树种相比，虽然樟子松的天然林面积和蓄积量较小，但樟子松具有较强的耐寒、耐旱、耐贫瘠土壤，较速生、树干通直，材质良好等特性，适合沙地生长，在中国北方，尤其是干旱、半干旱风沙地区，已经成为营造防风固沙林、农田草牧场防护林、水土保持林和用材林的主要树种。自

20世纪90年代初以来，最早引种的樟子松人工固沙林出现了大面积的衰退死亡现象以来，很多学者从栽植密度[2]、群落稳定性[3]、林木生长状况[4,5]、水分胁迫[6]、水分亏缺[7]等角度分析了沙地樟子松死亡原因，但栽植密度大小、群落稳定与否、林木生长状况好坏，水分亏缺与否，归根到底还是树木本身的水分平衡问题。研究树木的水分平衡比较复杂，从植物对水资源的利用情况看，凡影响光合、蒸腾和蒸发过程的环境因素均影响水分利用效率，主要有大气、土壤和栽培等管理因素[8]，在地下水埋浅且处于生长季节的高密度的乔木林植物蒸腾作用强烈，蒸腾消耗的水分最多[9]。树木的蒸腾耗水的测定目前最精确的测定方法为热扩散式探针法(thermal dissipation probe method，即TDP法)，该方法从原理上克服了蒸腾量测定的系统误差，但需要测定树木的边材面积，因此，边材厚度的测定成了影响蒸腾测定的中心工作[10-12]。如何测定边材厚度，由单木如何进一步推测整个林分的边材面积也是一个亟待解决的问题。不少专家学者试图通过边材厚度与其他易测因子之间的定量关系，通过测定一些易测因子来推导边材面积，从而测定整个林分的蒸腾耗水量。Hatton 等研究表明，边材面积与蒸腾量之间、胸径与蒸腾量之间均呈现明显的线性关系[13]。我国在这方面的研究起步较晚，马履一等[14]对油松(Pinustabulaeformis)、刺槐(Robiniapseudoacacia)、翟洪波等[15]对油松、栓皮栎(Quercusvariabilis)等进行了初步研究，但还没有研究樟子松边材面积与其他易测因子的相关报道。基于此，本文从不同林龄、不同方位研究了樟子松的边材宽度与胸径的相互关系，为樟子松林分蒸腾耗水量的研究奠定基础，为科学经营和利用当地森林提供科学依据和基础数据。

1 研究区概况与研究方法

1.1 研究区概况

试验地位于辽宁省固沙造林研究所章古台试验基地(42°43′ N，122°22′ E，海拔226.5 m)，属科尔沁沙地的一部分，年平均气温5.9 ℃，极端最高温度43.2 ℃，极端最低温度-33.4 ℃，≥10 ℃的年积温为3 148 ℃。年降水一般在450～500 mm左右，降水变率大，最大年降水量为744.8 mm，最小年降水量为262.3 mm，各季分配不均，70%以上集中在夏季。每6～7 a出现1次干旱年，近年来干旱频率增大。年蒸发量1 300～1 880 mm，约为年降水量3倍，相对湿度59%，旱季长达9个月。章古台地区冬季以西北和偏北风为主，平均风速3.3 m·s-1；春季多南风、偏西南风，风力大，持续时间长，风速为4.5～5.0 m·s-1，最大风速达25 m·s-1，年风速≥3 m·s-1的日数为160 d，春季6级以上大风日为46 d。年日照时数2 680～2 853 h。早霜在9月底或10月初，晚霜在4月中下旬，无霜期150～160 d。土壤为生草风沙土，主要代表性植物有色木(Acermono)、山里红(Crataeguspinnatifida)、家榆(Ulmusmacrocarpa)、大果榆(U.macrocarpa)、山杏(Armeniacasibirica)、胡枝子(Lespedezabicolor)、小黄柳(Salixgordejevii)、差巴嘎蒿(Artemisiahalodendron)、中华隐子草(Cleistogeneschinensis)、小叶朴(Celtisbungeana)、花曲柳(Fraxinusrhynchophylla)等。

1.2 研究样地与研究方法

在立地条件类似、相互间距小于3 km的10、30、40年生樟子松纯林中，各选取1块20 m×20 m、地势较平坦、树木生长状况良好的林地作为试验样地，所选试验样地距离林分边缘均大于50 m。由于20年生樟子松纯林生长状况良好的较少，且林分密度较小，故在20年生樟子松纯林中，选取1块10 m×20 m的样地，其它条件与其他三块不同龄级标准地一致。首先对标准地进行每木调查，以2 cm为单位进行径阶整列，计算每个径阶里树木的平均胸径，找出该径阶里与平均胸径最接近的个体，用生长锥在树干的胸高位置(去树皮)钻取直径为5 mm，东、西、南、北4个方位的生长芯，根据心材与边材颜色差异区分边材与心材间的界限，用螺旋测微器测量生长芯的边、心材半径值进行统计分析，数值不包括树皮厚度。以下平均心材与平均边材均简称心材与边材。表1为标准地林分基本特征，其中10 a、20 a、30 a、40 a分别表示10 a、20 a、30 a、40 a的樟子松样地。

表1 标准地林分基本特征

用Excel2003对边材宽度与胸径关系进行相关分析，通过相关性分析，确定龄级、边材面积、胸径之间的相关性，绘制樟子松边材面积与胸径关系的散点图，选择最优生长曲线建立数学模型。数学模型的评价指标采用决定系数(R2)，确定模型后对其进行显著性检验，并加以评价。用于拟合的曲线类型见表2。

表2 胸径生长曲线拟合方程

注：Y为边材厚度；X为胸径；a、b、c为待求参数

2 结果与分析

2.1 心材、边材的生长与径生长特征

心材宽度以逐年递增的趋势增长，在30～40 a时增长数值最大；边材宽度除30 a外均以递增的趋势增长，10 a以前和30～40 a增长数值大；10 a前、30～40 a 径生长较大(表1)。

2.2 10 a樟子松边材宽度与胸径关系

10年生樟子松在4个方位胸径与边材厚度均成极显著(P<0.01)的正相关。用5种不同的曲线拟合4个方位二者之间的关系(图1，表3)，结果显示：4个方向的边材厚度与胸径关系的最优生长曲线均为抛物线，可建立二次回归模型描述相关性，其拟合情况如表4。

表3 不同方位胸径与边材厚度5种曲线拟合R2值

由表4分析可知其中以西方位边材厚度与胸径之间建立的抛物线方程的拟合程度为最大(R2=0.975 3)，东方位边材厚度与胸径之间的拟合程度最小(R2=0.818 9)。4个抛物线方程经F检验后，结果均存在显著性差异，故上述建立的抛物线方程均可以比较准确的描述不同方位边材厚度与胸径间关系。

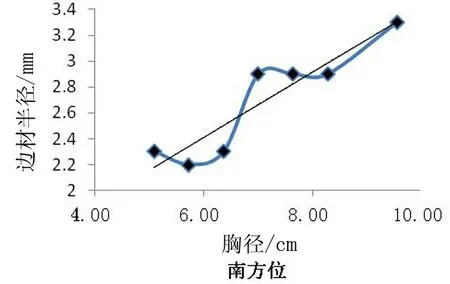
图1 不同方位边材宽度与胸径的拟合模型

方向R2方程东0．8189y=0．0459x2-0．3105x+2．8282南0．8624y=-0．0008x2+0．645x+0．8502西0．9753y=0．146x2-1．5546x+6．4017北0．8535y=0．1774x2-2．0929x+8．8473

2.3 20年生樟子松边材厚度与胸径的关系

相关分析结果显示东方位的胸径与边材厚度呈显著(P<0.05)的正相关关系，相关系数R为0.699 5。用5种曲线拟合东方位边材厚度与胸径之间的关系(如图2，表5)，结果显示：抛物线对东方位边材厚度与胸径之间的关系拟合的最好，R2值为0.669 7。东方位的边材厚度与胸径关系的最优生长曲线为抛物线，可建立二次回归模型描述相关性，其方程为y=-0.057 6x2+1.456 1x-4.761 9，经F检验，存在显著性，故可用此抛物线方程由胸径预测东方位的边材宽度值。

表5 东方位边材宽度与胸径5种曲线拟合的R2值

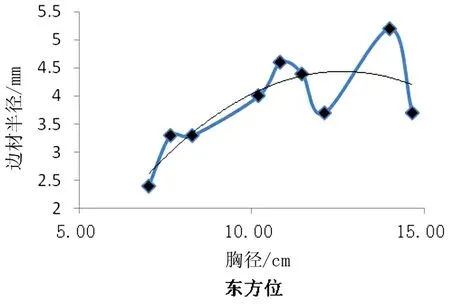
图2 东方位边材厚度与胸径的抛物线模型

2.4 30年生樟子松边材厚度与胸径关系

对30年生樟子松每个方位的边材厚度与胸径相关分析的结果显示东、南、西、北四个方位的胸径与边材厚度均存在显著(P<0.05)的正相关关系。其中东方位边材厚度与胸径之间呈极显著正相关(P<0.01)。用5种不同的曲线对30年生樟子松林东、南、西、北四个方位的边材厚度与胸径二者之间的关系进行拟合，拟合情况见表6。

表6 不同方位胸径与边材厚度5种曲线拟合R2值

图3显示：东方位边材厚度与胸径5种曲线拟合的拟合优度都大于0.5，说明可以用这5种曲线拟合东方位边材厚度与胸径之间关系，指数方程、抛物线方程、线性方程、幂指数的拟合效果R2值都很接近，进行F检验，存在显著性差异。图4表明，南方位抛物线、指数、线性图形对二者间的拟合优度值都在0.5以上，说明南方位边材厚度与胸径之间用这3种曲线进行拟合都可以，拟合效果为南方位抛物线、指数、线性方程的拟合优度R2值都很接近，进行F检验，存在显著性差异。用这几种类型方程均可描述30 a樟子松边材厚度与胸径之间关系，相应的方程表达式如下表7。对于西、北方向：表7中结果显示，30 a樟子松边材厚度与胸径间的5种曲线拟合中拟合优度R2均小于0.4，说明边材厚度与胸径在西、北方位用这5种曲线方程并不能可靠的描述出来。故不建立二次模型进行预测。

图3 东方位边材厚度与胸径不同曲线拟合图

方位类型R2值表达式东线性方程0．7236y=0．2423x-0．2177抛物线方程0．7296y=0．0068x2+0．0607x+0．9284指数方程0．7337y=0．9811e0．0811x幂指数方程0．7077y=0．2148x1．0137南抛物线方程0．5187y=0．0009x2-0．07x+1．9404指数方程0．5164y=1．0827e0．0654x线性方程0．5037y=0．1691x+0．4314

图4 南方向边材厚度与胸径曲线拟合图

2.5 40年生樟子松边材厚度与胸径的关系

边材厚度与胸径相关分析结果显示，东、南、西、北四个方位40年生樟子松胸径与边材厚度均成极显著(P<0.01)的正相关关系。西方位的相关性最为显著。用5种不同的曲线拟合东、南、西、北四个方位其二者之间的关系(如图5，表8)。

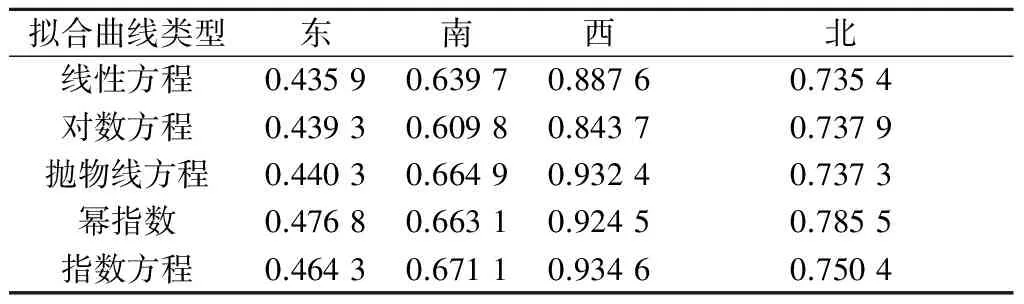
表8 不同方位胸径与边材厚度5种曲线拟合R2值

结果显示：用于东方位边材厚度与胸径之间拟合的5种曲线中，只有幂指数的拟合优度大于0.5，指数曲线的拟合优度接近0.5。南方位边材厚度与胸径5种曲线拟合中，抛物线、幂指数、指数图形对二者间的拟合优度值都在0.6以上(表8，图5)，尤其指数方程的拟合优度达到了0.67以上。西方位材厚度与胸径5种曲线拟合中，抛物线、指数图形对二者间的拟合优度值都在0.93以上。北方位边材厚度与胸径5种曲线拟合中，幂指数图形对二者间的拟合优度值最大。上述这些方程在进行F检验后，均有显著性差异，表明这些方程在描述不同方位40年生樟子松边材厚度与胸径间关系的适用性。相应的表达方程式见表9。

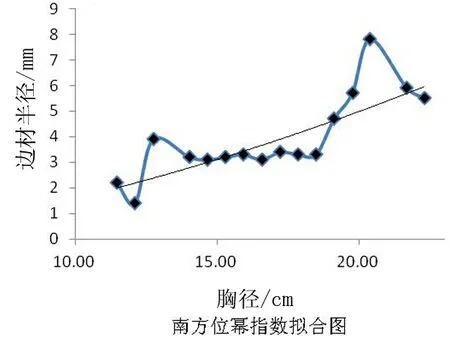
图5 南方位边材厚度与胸径曲线拟合图

方位拟合曲线类型R2表达式南抛物线方程0．6649y=0．0242x2-0．4294x+4．0648幂指数0．663y=0．0368x1．6386指数方程0．6711y=0．666e1．101x西抛物线方程0．9753y=0．1462x2-1．5546x+6．4017指数方程0．9381y=0．8385e0．1759x

3 结论与讨论

3.1 边材的生长特征

边材宽度变化规律间接反映了该树种生长规律：树木在达到一定年龄(心材起始树龄)或直径(心材起始去皮直径)之后，边材以相对稳定速度向心材转化(20～30 a)，随着树木年龄或直径的增长，树冠越来越大，维持整个树体生理活动所需要的输导组织越来越多，边材面积不断增加(30～40 a)，径生长速度加快。

3.2 不同方位边材宽度与胸径的关系

不同林龄的樟子松边材厚度与樟子松胸径存在显著相关性，10 a樟子松边材厚度与胸径的最优生长模型符合抛物线模型，拟合优度均大于0.7，抛物线方程为y= 0.146 2x2- 1.554 6x+ 6.401 7(R2=0.975 3)拟合效果最好。20 a樟子松中最优生长方程为抛物线方程y=-0.057 6x2+1.456 1x-4.761 9(R2=0.669 7)。30 a樟子松中只有东、南两个方位边材厚度与胸径关系可用曲线拟合，东方位符合指数方程y= 0.980 1 e0.081 1x(R2=0.733 7)，南方位符合抛物线y= 0.009x2- 0.07x+ 1.940 4(R2=0.518 7)或指数方程y= 1.082 7 e0.065 4x(R2=0.516 4)。40 a樟子松东方位为幂指数y= 0.196 5x1.077 2(R2=0.476 8)，南、西方位的指数表达式分别为y= 0.673e0.104 7x(R2=0.750 4)和y= 0.455 8 e0.123 8x(R2=0.934 6)，北方向为幂指数y= 0.029 1x1.748 8(R2= 0.785 5)，其中西方位的回归效果最好。

[1] 王兴昌，王传宽，张全智，等.东北主要树种心材与边材的生长特征[J].林业科学，2008,44(5)102-108

[2] 曾德慧,姜凤岐,范志平,等.沙地樟子松人工林自然稀疏规律[J].生态学报,2000,20(2):235-242

[3] 曾德慧,姜凤岐,范志平,等.樟子松人工固沙林稳定性的研究[J].应用生态学报,1996,7(4):337-343

[4] Zhu Jiaojun, Fan Zhiping, Zeng Dehui, et al.Comparison of stand structure and growth between artificial and natural forests ofPinussylvestrisvar.mongolicaon sandy land[J]. Journal of Forestry Research, 2003, 14(2): 103-111

[5] 康宏樟,朱教君,许美玲.科尔沁沙地樟子松人工林幼树水分生理生态特性[J].干旱区研究,2007,24(1):15-22

[6] 张继义,赵哈林,崔建垣.科尔沁沙地樟子松人工林土壤水分动态的研究[J].林业科学,2005,41(3):1-5

[7] 雷泽勇,刘心玲,周凯,等.辽西北沙地人工林植物水分亏缺与恢复研究[J].水土保持学报,2009,23(4):86-90

[8] 王韶唐.植物水分利用效率与旱地农业生产[J].干旱地区农业研究,1987(2):67-80

[9] 阿拉木萨,蒋德明,李雪华,等.科尔沁沙地典型人工植被区土壤水分动态研究[J].干旱区研究,2007,24(5):604-609

[10] Granier A, Biron P, Brénda N, et al. Transpiration of trees and forest stands: Short and long-term monitoring using sap flow methods[J]. Global Change Biology, 1996, 2: 265-274

[11] Oliveras I, Llorens P. Medium-term sap flux monitoring in a Scots pine stand: Analysis of the operability of the heat dissipation method for hydrological purposes[J]. Tree Physiol, 2001, 21: 473-480

[12] Lu P, Urban L, Zhao P. Granier’s thermal dissipation probe (TDP) method for measuring sap flow in trees: Theory and practice[J]. Acta Botanica Sinica, 2004, 46(6): 631-646

[13] 王华田,马履一.利用热扩式边材液流探针(TDP)测定树木整株蒸腾耗水量的研究[J].植物生态学报,2002,26(6):661-667

[14] 马履一,王华田,林平.北京地区几个造林树种耗水性比较研究[J].北京林业大学学报,2003,25(2):1-7

[15] 翟洪波,李吉跃,聂立水.油松栓皮栎混交林林地蒸散和水量平衡研究[J].北京林业大学学报,2004,26(2):48-51

Correlations between Sapwood Thickness and DHB ofPinussylvestrisvar.mongolicain Sandy Land

Zhou Fengyan

(Liaoning Provincial Dune-Fixation and Afforestaiton Institute , Fuxin 123000 , China)

DBH & sapwood of 10, 20, 30 & 40-year-oldPinussylvestrisvar.mngolicasand-fixation forest were determined under the same site conditions.Growth features of sapwood with different ages,correlations between thickness of sapwood and DBH at different ages were analyzed.Result shows that mean sapwood width of 10-year-oldPunussylvestrisvar.mongolicais 6 cm;the increase of mean sapwood is little at 20-30year-old; the increase of mean sapwood is great at 30-40-year-old;correlations between sapwood thickness & DBH of 10,20-year-oldPinusSylvestrisvar.mongolicacoincidence parabolic model,the fitting equation isy=0.146 2x2-1.554 6x+6.401 7(R2=0.975 3), andy=-0.057 6x2+1.456 1x-4.761 9(R2=0.669 7), respectively.Sapwood thickness & DBH of 30-year-oldPinussylvestrisvar.mongolicacan be fit by curve in eastern and sorthern bearing,the eastern bearing coincidence exponential model , the model isy= 0.980 1e0.081 1x(R2=0.733 7), the southern bearing coincidence parabolic equation:y= 0.009x2- 0.07x+ 1.940 4 (R2=0.518 7) or exponential equationy= 1.082 7e0.065 4x(R2=0.516 4; sapwood thickness and DBH of 40-year-oldPinussylvestrisvar.mongolicacan be fit by power exponent in eastern and northern bearing,being y = 0.196 5x1.077 2(R2=0.476 8)and y = 0.0291x1.748 8(R2= 0.785 5)respectively;the correlation of southern bearing and westen bearing can be fit by exponent model,the expression isy= 0.673e0.104 7x(R2=0.750 4)andy= 0.455 8 e0.123 84x(R2=0.934 6). The significant differences in width of sapwood with different ages can reflect the characteristics of their growth status, water use countermeasures, and material production.

sapwood thickness;Pinussylvestrisvar.mongolica; DHB; sandy land

1005-5215(2017)04-0048-06

2017-

周凤艳(1969-)，女，大学，高级工程师，主要从事林木遗传育种与荒漠化治理等研究,Email:fengyanzhou@sohu.com

S791.253

A

10.13601/j.issn.1005-5215.2017.04.017