沉降徐变的耦合受力性能分析
2017-04-27樊天望
樊天望
同济大学桥梁工程系
沉降徐变的耦合受力性能分析
樊天望
同济大学桥梁工程系
在桥梁设计时,沉降一般认为是瞬时发生的,而对于粘性土来说,达到最终沉降的时间很长,因此研究沉降的时变特性是有重要意义的。本文以一座两跨连续梁为例,进行考虑沉降时变特性和不考虑沉降时变特性的结构内力的理论上的推导,对沉降和收缩徐变耦合作用下的结构受力性能进行研究分析,并提出对基础不均匀沉降作用的折减系数。
沉降;徐变;耦合;理论推导;受力性能;影响因素
0 前言
桥梁结构由于上部结构、桥梁墩柱以及承台等的存在,对土会产生附加压力,造成一定数值的沉降,这在桥梁设计中体现为基础变位作用。在桥梁设计中,一般认为基础变位是瞬时发生的。对于砂性土而言,可认为这基本符合实际情况,但对于黏性土来说,达到最终沉降的时间很长,有时候能达到数十年,在这种情况之下,在桥梁设计时,能否简单地认为支座沉降是瞬时发生,而不考虑其长期时变效应,有待研究。此外,在沉降过程中,对于混凝土桥梁而言材料的收缩徐变也在发生,若考虑在沉降发生时收缩徐变同时发生,沉降对于桥梁结构的内力影响如何,更是有待分析。若考虑沉降时变效应下的收缩徐变作用,会影响结构的最不利受力,这将对结构的设计优化、材料节省及结构的准确分析等,产生积极有益的影响。因此本文以一座跨度为 和 的两跨连续梁为例,进行考虑沉降时变特性和不考虑沉降时变特性的结构内力的理论上的推导,对沉降和收缩徐变耦合作用下的结构受力性能进行研究分析,并提出对基础不均匀沉降作用的折减系数。桥梁结构示意图如图1所示:
假定此桥为一次落架,且假定此桥成桥内力为0,主梁刚度为EI,沉降时变规律为:,且不考虑收缩产生的内力及变形。
以下计算基于以上的假定。
1 不考虑沉降时变时的结构内力
在不考虑沉降时变特性时,可认为沉降为瞬时发生,之后再在此初始内力的基础上发生收缩徐变。因此可分为以下两部分进行计算:
1.1 瞬时沉降产生的结构内力
计算结构在瞬时沉降作用下产生的结构内力。此为超静定结构,取中间支座处的弯矩为未知量,基本结构如图2:
由相对转角为0可得力法方程为:
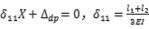
由几何关系可知,中间支座沉降Δ0时,有:

将以上两式代入力法方程中,可得:
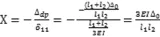
1.2 t1时刻的结构内力
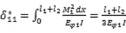
其中Eφ1为换算弹性模量Eφ1=γ (t1,τ0)E=
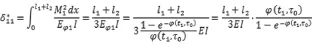

代入力法方程中,可得:

此即为徐变内力。可知徐变次内力和沉降产生的结构内力方向相反。同时徐变次内力和沉降产生的初始弹性内力成正相关。
根据以上计算,可知t1时刻中间支座处的内力为:
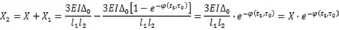
可知,t1时刻的内力为,为初始内力的,且内力一直变小,这与我们的理论知识相符合。
2 考虑沉降时变时的结构内力
考虑沉降时变特性时,认为沉降时变规律和徐变规律一致,假定最终沉降为Δ0,则t时刻值其沉降值为:
同上,取中间支座处的弯矩值为基本未知量,如图3所示:

图1

图2

图3
根据换算弹性模量法以及力法的基本概念,可建立相应的力法方程:
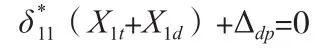
其中,X1d为在t时刻中间支座处由于支座沉降产生的弹性内力,而X1t为t时刻的徐变次内力。而t时刻内力之和为=X1t+X1d,因此力法方程可写为:


Δdp为支座沉降产生的相对转角,由几何关系可知:
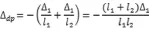
将以上两式代入力法方程中,可得:
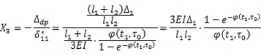
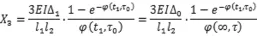
由上式可知,t1时刻的中间支座处的内力可知随着时间的推移结构内力越来越大。
3 内力比较
由以上两种情况下的结构内力理论计算可知,不考虑沉降时变特性时t1时刻中间支座处的内力为,考虑沉降时变特性时t1时刻中间支座处的内力为,两者之间的比值为:
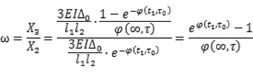
由比值可以看出,开始一段时间的同一时刻考虑沉降时变特性的内力要比不考虑沉降时变特性的内力要小,一段时间之后,同一时刻时考虑沉降时变特性的内力要比不考虑沉降时变特性的内力大。这是符合理论情况的,因为最初不考虑沉降时变特性时认为沉降终极值是瞬时发生的,相比较考虑时变特性的沉降产生的内力自然是要大的,因此最初一段时间考虑沉降时变特性的内力要比不考虑沉降时变特性的内力要小,过了一定时间之后,随着考虑时变特性的沉降大部分完成,沉降产生的弹性内力相差不大;同时初内力较大时徐变内力也同样较大,因此不考虑时变特性时徐变次内力要比同一时刻考虑沉降时变特性的内力大,对沉降产生的弹性内力减小的更多,因此后期同一时刻考虑沉降时变特性的内力要比不考虑沉降时变特性的内力大。
同时可以看出,两者之间的比值只取决于徐变系数的变化规律以及徐变系数终极值,与终极沉降值的大小、跨径的大小以及两跨连续梁的相对大小无关,影响两者比值的因素只取决于徐变系数,也即取决于影响徐变系数的因素。
当然,跨径以及终极沉降值不影响两种情况下的比值,却都会对结构的内力值产生一定的影响。跨径减小时,线刚度变大,因此同样沉降值情况下内力变大;而沉降值越大内力也越大,从以上两个结构内力的公式也可以印证这一结论的正确性。
