基于不同极值分布下输电线路覆冰重现期的对比分析
2017-04-27邓鹏飞容洁王建城苏盛
邓鹏飞 容洁 王建城 苏盛
摘要:该文选取湖南永州气象观测站覆冰数据进行基于年极值法、跨阈法和独立风暴法的导线覆冰极值冰厚抽样,然后利用极大似然估计法进行广义极值分布和广义帕雷托分布拟合,进而估计多年一遇线路覆冰极值。对比分析表明,三种取样抽样方法中,基于广义极值分布的年极值抽样法可以较好地拟合电线积冰观测序列,对永州站覆冰冰厚极值的拟合精度最好。计算结果也较为接近其数学期望,可为输电线路设计提供参考依据。
关键词:覆冰;广义极值分布;广义帕雷托分布;重现期
中图分类号:TM731 文献标识码:A 文章编号:1009-3044(2016)29-0251-03
输电线路覆冰严重会对电网的稳定运行构成重大威胁。多年一遇极值冰厚的准确估计是确定输电线路规划设计标准的重要基础。
传统上输电线路多年一遇极值覆冰多采用极值Ⅰ型分布,但也有看法认为不同类型的覆冰有不同的极值分布。在极值风速等研究领域,也有研究人员认为采用跨阈法(POT)等方法能更好地分析极值事件。进行输电线路设计时,需考虑线路覆冰荷载,预估寿命周期可能出现的最大覆冰重量,并根据线路等级进行采用不同重现期设计荷载。目前,我国确定覆冰荷载的方法大多是根据实地调查结合附近气象资料作经验估算,但与之矛盾的是,进行导线积冰观测的气象台站较少,观测年限大多较短,而导线覆冰的设计荷载常需要几十年甚至上百年重现期下的数据。本文应用极值分布理论,对我国永州气象观测点电线积冰基于不同极值分布加以研究,具有十分重要的意义。
1资料和方法
1.1资料
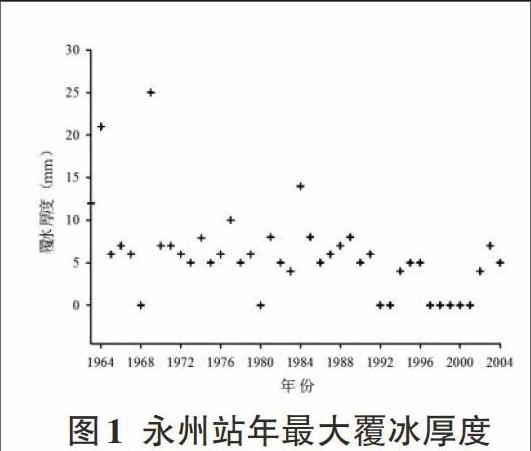
选取湖南永州气象站1963-2004年线路覆冰数据展开研究。该站地处湘西南部,北纬26°14′、东经111°37′,海拔157.3m,42 a间均有积冰记录共计113次,记录连续性较好。其年最大覆冰记录绘制如图l所示。
由图1可见,该站覆冰数据序列连续,年极值覆冰在6-8mm左右,1969年曾一度达到25mm,之后有逐年下降的趋势,每年最大覆冰厚度从5mm-15mm变化,覆冰厚度不大,下降斜率为-0.163。
1.2方法
本文基于永州站气象台站的观测数据序列,通过极值理论,在对原始资料分析、整理和求出其经验频率的基础上,使用年极值抽样法、POT法和MIS法挑拣极值样本数据,然后使用GEV和GPD极值分布函数,利用极大似然估计法对输电线路覆冰极值序列加以拟合,来求解永州站基于五十年一遇重现期的线路覆冰,探寻适合拟合线路覆冰的分布模型。
1.2.1年极值抽样法
年极值抽样法是一种经典的取样方法,即基于极值分布的年最大值抽样方法。对于一定时间段内的输电线路覆冰厚度样本X1,X2,X3,,,Xn,其积累函数设为F(x),并设最大覆冰厚度为Mn=max(X1,X2,,,Xn),从原始数据中选取出每一年的最大值进行分析,由极值理论可以知道,每一年的最大覆冰厚度Mn的分布渐近为P(X):
1.2.2跨阈法(POT法)
跨阈法是建立在时段最大值的取样方法之上的。为了更加合理利用现有数据资料,其基本思想是应用Pareto分布去模拟超越阈值的峰值覆冰。本文中,POT法就是对覆冰厚度总体的样本选取某一个特定的阈值u,并认为超越阈值u的覆冰厚度服从泊松分布,当n趋于无穷大时,覆冰厚度的值渐近服从广义Pareto分布,跨阈值法事实上较年最大值法的广义极值分布要方便。
1.2.3独立风暴法(MIS法)
Cook应用独立风暴法提取样本并应用Gumbel分布依据阈值u划分成独立的风暴。不同于POT法,MIS只考虑每个独立风暴的最大值作为一个极值样本。MIS假设T年中有n个独立风暴,即n个极值样本高于阈值u,则单个独立风暴的极值分布为Fx(x)由公式(1)得到下式:
(2)
同时MIS法对于极值样本可以采用多种分布而不局限于廣义Pareto分布。
2导线覆冰极值概率分布的拟合
2.1 GEV、GPD概率分布模型及其参数估计
极值的渐近分布可以将3种类型的经典极值分布表示成一个统一的具有3参数的分布函数,广义极值分布(简记为GEV)。设X1,X2,X3,,,Xn,是服从GEV分布的独立随机变量,则广义极值分布的分布函数为如下公式:
(4)
(5)
常用的参数估计方法有矩法、最小二乘法和极大似然法等。本文采用极大似然估计法来估计参数,它的结果在总体上反映样本的统计信息,具有良好的统计性质。
2.2重现期水平
在计算得到分布参数后,即可对给定的频率T求解其对应的分位数XT,对于输电线路极值分布模型建立的根本目的在于推断重现期概率下极值变量的可能取值。GEV分布T年重现期的冰厚极值估计式为:
(6)
(7)
GPD分布重现期冰厚极值的估算公式为:
(8)
(9)
式中σ为尺度参数,μ为位置参数,ε为形状参数。λ为年交叉率,表示为λ=m/n,其中m为超过门限的极值数量,n为资料记录的总年数。
3计算及分析结果
3.1重现期分析
利用年极值法处理得到的数据分别符合GEV和GPD、而用POT法和MIS法得到的数据符合GPD分布,利用极大似然估计法求出参数,再根据公式算出基于不同分布下的10、20、50、100年不同时间间隔内的重现期水平。
通过使用GEV、GPD模型,利用统计软件R来计算覆冰厚度极值,计算出轮廓数似然曲线与水平线有三个交叉点。在顶部水平线的交叉点表示基于50年重现期水平预测下的覆冰厚度极值,而在底线的两个交叉点表示95%的置信区间的上限和下限。由分析可见,基于GEV分布的年最大值法的50年重现期水平与前述42年的实际观测数据最为接近。选用50年重现期水平位主要考量指标,得到如下参数如表1,对数据进行分析表明:
1)随着重现期间隔的增长,重现期水平不断增大,但GEV分布基于年最大抽样法的重现期增长速度不大。通过年最大值法抽取数据后,用GEV分布比GPD分布的拟合效果好,且GEV分布随T的变化而不断增大,其他分布则变化不大。
2)基于GEV分布的年最大值抽样法的ε为正,其他几种为负。样本容量达到25a左右时,广义帕雷托分布重现期冰厚极值的估计趋于稳定,可以作为短序列下估计导线覆冰极值的较好方法。
3)采用极值分布拟合的方法可以计算长于观测年限的重现期下极值情况,计算结果也较为接近其数学期望,可以为实际应用提供参考。
3.2诊断结果分析
Q-Q图是一种图示化检验方法,可用来检查基于GEV、GPD假设下的极端数据超过设定阈值的有效性。当X的分布函数为F(x)时,Q-Q图近似为直线,如果Q-Q图偏离线性,则表示所选的分布F并不合适,基于不同分布的Q-Q图被绘制在图2中。
由图2可见,基于GEV分布的诊断图中,数据点大部分游离在拟合直线附近,而POT法和MIS法的数据点明显偏离拟合直线,拟合效果远不如基于年极值法的GEV分布,GEV分布相对于GPD分布,能够更好永州站的覆冰数据。三种方法中,年极值法的拟合效果对两种分布在导线覆冰极值模型拟合的适用性研究表明,广义极值分布对永州站覆冰冰厚极值的拟合精度最高。
4计算及分析结果
本文选用三种取样方法,通过基于GEV分布和GPD分布拟合数据分析,笔者认为输电线路覆冰数据中,基于GEV分布的年最大值抽样法的拟合效果明显的比GPD分布好,能够很好地拟合实际数据。三种分析方法中,重现期冰厚极值估计随样时间间隔的变化分析表明,GPD模型极值估计的稳定性优于GEV,一般樣本容量达到25a左右时,GPD重现期冰厚极值的估计趋于稳定,可作为短序列下估计导线覆冰极值的较好方法。在本文中,基于GEV分布的年最大值分析方法能够很好地拟合输电线路覆冰数据,
能较精确地估计重现期水平,对湖南部分地区输电线路覆冰载荷的设计具有一定的参考意义。