黑白棋AI设计探究

黄海同

摘要：与博弈有关的算法近年来取得了巨大进步，将这些算法应用于黑白棋AT设计可以带来显著的效果。该文所述的探究中，将传统的AI算法针对黑白棋做一些有效的改进，并使用MCTS搜索、机器学习等方法，很大程度上提高了AT的水平。

关键词：黑白棋；人工智能；算法

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2016）29-0198-03

1简介

黑白棋是被称为“设计理念”仅次于围棋的棋类游戏。它的棋盘只有8*8大，乍一看貌似简单，以为只要略微搜索就可以穷尽其中的路数。然而随着探究的不断深入，这个看似简单的游戏却不断涌现出它神秘莫测的一面。

作为一名高中生，经过为数不多课余时间的努力，我所设计的黑白棋程序bwcore实力已经达到相当的水平。经测试，它在北京大学人工智能对抗平台botzone.org上战力排行达到第一。通过与另外一些AI的测试表明，目前的bwcore可以轻易打败国内个人编写的程序，亦能与专业公司开发的黑白棋软件（zebra，伤心黑白棋等）相抗衡。

本篇着重讲述了bwcore是如何更好地运用各类算法，使之融入到黑白棋AI设计中，达到提高AI水平的目的。本文还对AI设计作了一定程度的研究，先是介绍了一些较基础的算法在黑白棋AI设计中的应用，而后还探讨了实现AI的一些更高级的方法，以求有所突破。

2AI设计

2.1Minimax搜索

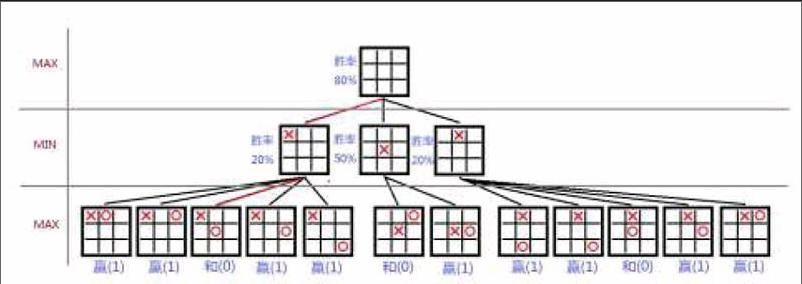
Minimax搜索的第一要义是双方都按照对自己最有利的决策，对盘面进行模拟。如果能够评价某一时刻其中一方的优劣程度，则另一方走棋时就会选一种使对方优势尽可能小的走法。如图所示，按照这种方式模拟出井字棋所有可能的局面，所有局面就构成一棵极大极小博弈树。

根据上述做法，不难写出简易MiniMax搜索的代码。当搜索达到指定深度后，进行当前局面的分值估算。val为当前层的分值，当前层的颜色与己方相同时，使之尽可能大。

float Cmp_BW：：MaxMinSearch（Map&fmap，int col，int deep）

{

if deep>target_deep Then

search_cnt++；

return Sence_Evalution

For-Each place_in_board

If place_is_availaleThen

MakeMove

ret=MaxMinSearch（board.color_other，deep+1）；

UnMakeMove

if col==my_color Then

2.2剪枝與改进

Minimax算法提供了一种在博弈树上寻求最优解的方法，但缺点很明显。算法需要遍历博弈树上所有可能的情况，尽管很多时候是根本不可能的（例如一方选择了一个明显劣势的位置）。通过AlphaBeta剪枝可以减少这种情况发生。如果当前结点获得的值已经小于其父节点之前得出的值，那么就没有继续搜索的必要，因为按照选择的逻辑，这个节点一定会被父节点排除在外。

经测试，搜索的节点数明显减少，约为原来的3/4次方。

测试表明，一般人已经难以战胜4～5层的搜索了。而把搜索深度设定为4层可以在botzone排行榜上达到约40名。

3高级搜索方法

3.1蒙特卡洛搜索

谷歌的围棋智能AlphaGo就使用了基于蒙特卡洛树搜索（MCTS）的搜索方式。MCTS在围棋领域十分成功，在其他方面也有很大的借鉴意义。

蒙特卡洛搜索通过对局面的随机模拟来获得对各个节点搜索的关注程度，可以说在理念上很接近人的思维方式。UCT算法是蒙特卡洛搜索的一种，旨在得分未知的前提下使期望得分最大。UCT算法为每一个节点计算UCB值，每次扩展时选择UCB最大的节点。

其中，X表示以前的收益，N表示总次数，T表示当前阶段的次数。这个式子的蕴含的内容是，如果一个节点的得分很高，那么就它很值得深入研究，而一些得分较低的节点有时也会去尝试，但次数不会很多。在极端条件下，多个选择方案中有一个方案的值远好于其他方案，则UCT算法的收敛速度很快。另一方面，如果所有方案得分相差不大，UCT随着搜索次数的增加，所有节点的得分趋于稳定。

结果表明单纯的UCT算法效率极高，经过很少时间就估算出精确值相近的结果。但因有时随机选点得出结果差异大，下棋时偶尔会出现失误。但总体而言，朴素的UCT算法的效果已经很优秀，测试过程中棋力超过前面基于MiniMax搜索的算法。可以想见，如果能在Simulation过程中加以优化，还有很大提升空间。

3.2遗传算法

遗传算法也是比较好的搜索方式，它通过借鉴生物界的进化规律来加强搜索。将前面的搜索局面各行列情况视为遗传算子，搜索过程中经过交叉、变异算子，评估新算子的可靠程度，将进化较成功算子反作用于搜索，每次得出更好的搜索方法。具体过程如下：

1）随机生成n个个体作为迭代的初始群体；

2）计算群体中每个个体的适应程度；

3）进行选择，把适应度高的个体的基因传递给下一代；

4）使新生成个体的基因交叉互换；

5）对基因做一定程度的变异；

6）返回2），除非适应度达到指定水平或已经达到最大迭代次数。

经过多次迭代，适应度高（这里即胜率高）的基因将遗传下来，最终得到高度适应的群体，即我们下一步所期望的走法。

4机器学习与增强学习

前面的几种搜索方法比原先单纯的搜索更具智能性，有更高的效率。目前为止，我们还未对局面的评估做出很好的改进。而估价函数的选取十分困难，大多依靠编写者自己的直觉，有时为了让某个权重来达到合适的值，还要耗费大量时间进行试验并调节。所幸，运用机器学习的方法可以使这些问题得到较好的解决。

4.1决策树与随机森林

决策树（Decision Tree）是其中一种比较简单的做法。决策树可用于对带标签数据的分类，并可以在相对短的时间得出效果良好的结果。依照数据标注的特点，决策树的每一个分支对这些样本进行划分，最终使样本按照标签归类。预测时，将想要预测的数据选择相应分支找到对应的归属即可。

在黑白棋中，如果将黑方获胜视为样本中的正类，白方获胜视为负类，棋盘上黑白棋子的位置作为样本的标签，就可以将对局面的评价转化为分类问题。决策树通过不停寻找最优分裂使数据更好地被分离。这里使用C4.5算法，通过信息熵获得最优分裂。由于单纯使用棋子的位置作为标签信息量较大且十分复杂，容易造成一种称为过拟合的問题。将决策树上改为随机森林，可以避免了过拟合，节约了训练时间。

4.2神经网络算法

人工神经网络是当下计算机话题最热门的内容之一。神经网络的种类繁多，BP神经网络是神经网络中最简单的一种模型。

BP神经网络的结构如图，左边为输入层节点，右边为输出层节点，中间包含一个或多个隐含层。

每个神经元从其上一层获得输入，将输入通过自身权值和阈值变换后施以适当激活函数，传递到下一次神经元。这样的过程称为正向传递（Fowed Transfer）过程。根据正向传递得到的网络输出与训练目标比较计算当前网络的误差，然后向前调整各个神经元权值，就是所谓的反向传递（Reverse Transfer）过程。BP网络不停通过这种方式训练减小误差，最终使每个训练输入都收敛于目标输出。

这里使用棋盘上黑白棋子的分布作为输入层节点，用01表示，输出层表示输赢棋子数。训练结果表明，虽然目前的网络能较好地拟合训练集中的局面，但对于推广与训练集不同的输入数据较为困难，这可能是因为当前所使用网络的局限性。此外，BP神经网络隐含层的层数不宜过多，否则收敛十分缓慢。使用深度学习中更高级的神经网络如卷积神经网络（CNN）等应该能够得到更好的效果，但过程比较复杂，目前个人难以实现。

4.3训练方式

学习算法需要进行训练，一种方式是使用接近后期时搜索得出的结果，这种方式获得样本的准确度较高。如果按照终局搜索步数15-20步计，训练好的AI将可以在近30步时获取很大优势。

//用后期对局结果作为样本训练

void Cmp_BW：：train（int repeat）

For lxain_count

For remain_step>target_step

run_easy（map）//使用简单方式下棋，节约时间

score=getScore（map）//获得比分

deetree.tmin（map，score）；//用样本训练

5总结

本次设计AI运行结果已经超过了预期的目标，此前没有想到过可以在排行榜占据第一的位置。当然，目前算法距离其所能达到的最高水准还有较大差距，因为看起来还有一些明显的改进方案。不过，作为一个纯属兴趣爱好出发而编写的程序，能够取得较好的结果已令人满意。由于无法在这方面投入太多的时间，所以目前本人对黑白棋AI的研究大致到此，希望将来能够继续深入探究这一方面的问题。