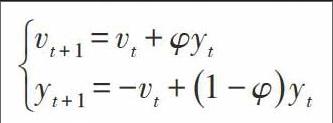PSO算法收敛性分析研究综述
2017-04-27陆伟峰
陆伟峰
摘要:粒子群算法是当前群智能计算中的一个热点。系统介绍了当前PSO算法收敛性分析中的一些重要研究方法,如常微分方程、Lyapunov稳定性理论、凸化理论、Markov链和随机逼近等方法。并指出未来研究的方向。
关键词:粒子群算法;收敛性分析
中图分类号:TP391 文献标识码:A 文章编号:1009-3044(2016)29-0181-02
粒子群算法(Particle Swarm Optimization,PSO)是模仿鸟类捕食行为的一种仿生算法.由于PSO收敛速度快、参数少简洁易操作,是求解连续优化问题的重要方法。但也存在着易陷入局部最优值、迭代后期搜索能力不强等缺陷。
为提高PSO的搜索效率,众多学者进行了研究,提出了各种改进方法。遇到的一个难题便是如何保证算法的收敛性。本文系统总结了近几年PSO收敛性分析方面的研究成果,指出了各种算法的特点。并对未来的研究进行了展望。
1PSO算法的原理
标准粒子群算法可以表述为:在,J维搜索空间中,m个粒子组成一个种群,t时刻第i个粒子的位置可以表示为Xit=(Xi1t,Xi2t,…,XiDt),飞行速度可以表示为vit=(vi1t,vi2t,…viDt),(i=1,2,…,m)。第i个粒子的历史最好位置记为Pib,整个种群的历史最优位置记为Pg。由于每个粒子是地位均等的,我们省略标号i得到每一代粒子的位置Xt和速度vt的迭代方程为:
其中ω为惯性系数,c1,c2为常数,通常记c1+c2=c,r1,r2为[0,1]之间的随机数。
c1r1(pb-Xt)是粒子的认知部分,体现了自身的经验。c2r2(pg-Xt)是粒子的社会部分,体现了粒子的交互能力。通过这两项,粒子协调局部与全局探索能力,从而达到全局最优值。
2PSO算法的收敛性分析研究进展
由于PSO算法是一个随机系统,受到随机系数的影响很大,分析比较困难。许多学者使用各种不同的方法对其进行收敛性分析,确定收敛的条件,指导算法的改进工作。
2.1基于定常线性系统的收敛性分析
最早并且最广泛采用的方法是将随机数看做常数,使用确定性线性系统的稳定性分析方法进行分析。
Clerc和Kennedy首先采用这一方法,假设Pb,Pg保持不变,r1,r2为常数,将基本粒子群算法表示为定常线性系统:
其中yt=p-xt。
通过计算特征系数矩阵的特征值小于1,确定收敛条件下参数的取值范围。
孙湘等在文献中不考虑随机分量,将带惯性权重的粒子群算法表示为一个线性系统:
根据动力系统稳定性理论,系统稳定的一个充分条件是系数矩阵的特征值λ1,λ2满足max{|λ1|,|λ2|}<1,由此得到系统稳定收敛的条件是0<ω<1且0 这一方法将随机系统转化为定常线性系统,简化了问题,但没有考虑随机分量,削弱了结论的适用范围。这些结论既不是充分条件也不是必要条件。 2.2基于随机过程的收敛性分析 文献将PSO算法化为 2.4基于凸化理论和概率收敛理论的收敛性分析 文献则使用凸性理论和概率收敛理论,分析得到在不考虑随机性的条件下,对于单峰值函数,粒子群收敛于全局最优位置,而对多峰值函数,未必能最终收敛于全局最优位置。在考虑随机性后,无论单峰值还是多峰值函数,粒子群都能依概率收斂于最优位置。 该方法较好的给出了收敛条件、收敛速度及误差估计。但是假设的前提条件比较多,需要进一步研究更一般的条件下的收敛性。 3总结与展望 本文对粒子群算法近几年有关收敛性分析方面的研究进展进行了概况和总结。由于粒子群算法是一个复杂的非线性随机系统,对其收敛性分析的研究还在不断深入。通过分析现有研究成果,对PS0收敛性分析的工作总体呈现以下趋势: 1)研究方法的不断拓展。目前的研究主要是常系数微分方程(差分方程)方法和基于随机过程的分析、基于Markov链的分析等随机分析方法。针对IX50算法的特点,随机逼近等随机方法将可能继续深入研究,Mann迭代序列等迭代算法可能用于PSO的收敛性分析。 2)从单粒子的收敛性分析,转向对整个粒子群的收敛性分析。基于定常线性系统、随机过程、Lvapunov等方法的分析,是对单个粒子的分析,虽然比较成熟,但无法反映整个种群的状况。而基于Markov链、基于随机逼近等方法分析了整个种群的收敛性,得到的结果更具一般性。 3)从基本PSO算法的收敛性分析,延伸到对PSO改进算法的收敛性分析,并用于指导算法的改进。从PSO算法诞生到现在,众多学者投入研究,引入量子行为、混沌等新的寻优机制,提出众多新颖有效的改进算法。这些改进算法的收敛性分析也必将成为研究的重点。而分析的结果也为提高算法的性能提供了理论依据,指导算法进一步提高收敛速度与精度。