思维导图

晋瑛

【摘要】复习课的目的是帮助学生梳理知识，构建知识结构。思维导图作为一种简单易行的思维工具，能有效提高学生的思维能力，帮助学生构建知识体系。

【关键词】思维导图；复习课；优势

什么是学习？著名认知心理学家、教育改革家布鲁纳主张学习的目的在于以发现学习的方式，使学科的基本结构转变为学生头脑中的认知结构。学习的实质是主动地形成认知结构，学习包括知识的获得、转化和评价三个过程。由此可见，学习总是一个循序渐进的过程，不可能一蹴而就。学习的过程就是一天学习一点点，每天将吸收到的新知纳入已有知识体系。尤其是小学生，每天学习的知识在头脑中总是散乱的、无序的、缺乏联系的。所以我们常常看到，每天的课后作业学生往往会完成得很好，因为那是简单的重复或是单一的模仿，然而每到综合性地考查学习情况时，问题就会层出不穷。因此，构建知识体系，建立知识间的联系十分重要。

作为小学数学教师，必须全面深入地分析教材，明确学科本身所包含的基本概念、基本原理及它们之间的相互关系，只有这样，才有可能引导学生加深对教材结构的理解。同时还应明确所要建构的学生的认知结构包含哪些组成要素，并最好绘制出各组成要素的关系图解。在此基础上，教师应采取有效措施来帮助学生获得、转化和评价知识，使学科的知识结构转化为学生的认知结构，使书本的死知识变为学生自己的活的知识。

一、怎样将思维导图运用在复习课的教学中

思维导图无疑是一件简单易学的革命性思维工具，通俗地说，是一个简单、有效、美丽的思维工具。我们尝试将思维导图运用在小学数学复习课中，取得了显著的效果。那么怎样将思维导图运用在复习课的教学中呢？

首先，要确定单元学习的关键词，也就是找出单元核心概念，放置在图画的中心位置，然后用椭圆圈上，或者以鲜艳的色彩加以强调。一切学习活动都围绕着个词语展开。

其次，从中心开始，画出一些向四周发散的线条，由核心概念展开联想，找出第二级关键词、第三级关键词、第四级关键词……在这个过程中，要善于运用想象力，尽可能多地找到与核心概念相关的知识，形成放射状的画面，其中尽可能运用图画的形式，或以色彩加以突出。

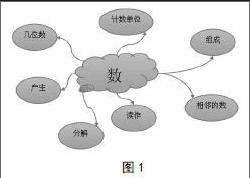
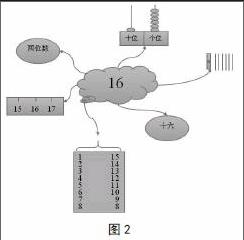
再次，以关键词展开联想形成的思维导图更多的是概念的结构图（图1），显得较为空洞，不具体。我们可以将该思维导图作为一个模板，以一个具体的数来举例，形成一个有具体数例的思维导图（图2）。

二、思维导图的优势

思维导图以开放发散的思维、形象生动的图形、简洁准确的关键词、鲜艳美观的画面……运用在小学数学复习课中，其优势具体体现在哪些方面？

（一）思维导图有效促进学生思维能力的提高

思维导图是从一个中心出发，通过联想和想象，发散出相关的若干枝节，从每一个枝节又再进一步发散。人的大脑的工作是运用图像和网络般的联想，而思维导图正是运用图像和网络般的联想，二者之间是完全吻合的。因此，思维导图的运用能很好地提高学生的发散思维能力。

从图1中我们可以看到，思维导图的中心是一个“数”字，学生从“数”这个词联想到数的组成、分解、读法、相邻的数、位数、计数单位、数的产生、数的用处、计算等。根据学生想到的，教师在黑板上逐渐呈现出一幅关于数的相关知识的思维导图。学生以此为模板，写一个自己喜欢的数，进行独立探究，可以进一步发散和创造。

（二）思维导图体现数形结合的思想，促进右脑的开发

思维导图最初源于学习笔记。利用图画的形式记录信息是思维导图很重要的方式。著名画家达﹒芬奇在他的笔记中经常使用图形、代码和连线，这些看似涂鸦，却能使笔记更生动活泼。人的大脑中，左脑主要负责理性、语言、文字、分析等，右脑主要负责音乐、形象、经验、直观等认识，因而右脑感觉更强，我们常说的“创造性思维”也更多是右脑的产物。数形结合的思想其目的就在于启发人的创造性思维。

那么如何开发人的右脑，使我们的学习更形象化呢？可以将图画引入我们整理的知识体系中。从图2可以看出，有的学生在表达16是一个两位数，它所占的数位是个位和十位時，没有用文字表达，而是画出一个计数器。从图画中，我们既可以看到它是一个两位数，而且数位顺序也清楚地排列出来，计数单位也清晰可见。在表达相邻的数是哪两个时，最初我也没有想好怎样表达。我想，要不就直接写出两个数“15、17”，要不就写一句话：“相邻的数是15、17”。有位学生说可以画尺子图。我还纳闷，又不比较大小，画尺子图干啥？真没想到学生创造性地用尺子图表示与16相邻的数是15和17，非常直观形象，将数和形有机地结合起来了。

（三）思维导图有效地帮助学生构建知识体系

数学知识有着严密的逻辑结构，不论是几何知识还是代数知识，其纵向发展都是一条有机的知识链。从横向上看，许多数学知识非常相似，彼此之间有着紧密的联系，对这些知识既要纵向连线，也要横向贯通，形成高层次的知识结构。思维导图能够非常有效地在知识与知识之间架起沟通的桥梁，沟通知识之间的内在联系。就拿上面的例子来说，学生已经充分感受到了自然数的神奇，仅仅10个数字就能够组成无数的数，可以大到无穷。这么神奇的自然数，应该从哪些方面认识它呢？数的产生、组成、计数单位、组成的数字、数的分解、读写等等，有太多可以联想到的，甚至有的学生想到了计算，得数是16的加法算式、减法算式有哪些。相信通过利用思维导图，学生能够在他的知识体系中构建出全面系统的数的认识，有利于促进学生数感的发展。

思维导图运用在复习课中，能够全面、开放、直观、形象地呈现大脑的思维过程，呈现知识间的内在联系。因此，思维导图是复习课的优选模式。