单开口膜泡形状转变的研究∗

2017-04-26梁月凤张劭光

物理学报 2017年15期

梁月凤张劭光

(陕西师范大学物理学与信息技术学院,西安 710119)

1 引言

近年来,人们对开口膜泡和黏附膜泡的研究有了较多的重视,这是因为膜泡的黏附不仅对膜泡适应周围环境有重要作用,而且在许多生命进程中是必不可少的,诸如细胞的外排和内吞以及膜的融合[1,2].黏附膜泡可以作为载体实现药物的输送[3,4],膜与固体基底(或媒的作用物)之间的作用机理可以应用于生物传感器[5,6].因此,研究生物膜泡的黏附具有重要的医学价值,对毒理学模型、人造器官、活性药物筛选等应用领域都有很重要的理论指导意义.

过去人们对黏附膜泡的研究集中于闭合形状.Seifert和Lipowsky[7]考虑了黏附能后提出了一个简化模型,最先对闭合黏附膜泡进行了较系统的计算;随后,Capovilla和Guven[8]从力学平衡的角度讨论了黏附边界满足的几何条件,测出了膜泡黏附在固定培养基上的黏附能;Tordeux和Fournier[9]提出一种测量黏附能的新方法,还通过控制黏附梯度提出一种测量小尺度黏附膜泡尺寸的方法;Rosso和Virga[10]研究了膜泡黏附在固定培养基上的平衡态.最近,Das和Du[11]研究了膜泡的转变和培养基形状之间的关系,他们还构造了一个预测膜泡形状的解析解.

近年来对开口膜泡的研究也取得了一些进展.实验上,Saitoh等[12]通过向水溶液中类脂膜泡加入一定浓度的类膜性质的蛋白质Talin分子,观察到了一些杯形、管状和双分子层等形状的开口膜泡.在理论研究上,Capovilla等[13]首先用场论方法给出了一般情况下开口膜泡的形状方程和边界条件;Tu和Ouyang[14]将外微分法用于处理曲面上的问题,给出了自发曲率(SC)模型下的形状方程和边界条件;Umeda和Suezaki[15]基于面积差弹性(ADE)模型首次用弛豫法数值计算得到了一些能够与实验上观察到的形状对应的球形附近的一些开口膜泡形状;Kang等[16,17]首先给出了哑铃形开口膜泡;孔祥波和张劭光[18]给出了双开口哑铃形,并研究了单开口和双开口及闭合哑铃形之间的相变;Ni等[19]研究了有黏附情况下的开口膜泡,并给出了一些形状.

目前还缺乏对开口膜泡及开口黏附膜泡的系统研究.关于开口膜泡的研究,也还存在一些问题:例如还没有在双层耦合(BC)模型下进行过计算,由于BC模型可以给出约化面积差,这是膜泡形状的一个重要参数,而且是实验可以测量的一个量,因而以往在研究闭合膜泡时一般是先给出BC模型下的相图,再在此基础上研究ADE模型的相图;而且目前得到的各支解的关系还不清楚;Umeda和Suezaki[15]宣称杯形膜泡可以连续地变为闭合球形,而开口膜泡和闭合膜泡处于不同的拓扑结构,它们之间是否能连续转变?另外他们得到的杯形解与Kang等[16,17]得到的开口哑铃形之间有什么关系?为何Umeda和Suezaki[15]宣称得不到这样的解?

另一方面对开口黏附膜泡的研究还很有限,为了研究开口黏附膜泡及其相图,首先应该找出尽可能多的分支解,并对解的行为有较全面的把握.

本文在BC模型下,通过系统地研究这些解随参数的演化行为来回答这些问题.第二部分先对BC模型及计算方法做一概述;第三部分别讨论在无黏附和有黏附模型下的计算结果;第四部分给出结论.

2 理论基础

2.1 BC模型

生物膜泡形状的曲率模型最初是为解释红血球的双凹形状而提出的[20,21],先忽略膜的厚度,把生物膜看成一个二维曲面,膜泡的曲率能为

其中C1和C2是两个主曲率,为平均曲率,K=C1C2为高斯曲率,kc为局域弯曲模量,kG为高斯弯曲模量.如曲面的拓扑结构不改变,由高斯-波涅定理,第二项贡献一常数,因而可以忽略.

再加上开口处的线张力能及黏附能,开口黏附膜泡的总能量可以表示为

(2)式中的第一项为曲率能,第二项为开口处线张力能,第三项为黏附能;γ是线张力系数,ω是黏附系数,A∗代表黏附面积,dl代表开口边缘处的长度微元.

再考虑双层膜之间的不对称性.一种方法是引入自发曲率C0,这是Helfrich[22]最先引进的,以解释铁饼及哑铃形状能量的简并,该模型称为SC模型.

另一种理解双层之间不对称的模型是BC模型[23,24].该模型认为膜泡形成时,两层的面积差保持不变,即假定在形变过程中两单层之间不交换磷脂分子,两单层之间的面积差在一级近似下可写为膜的厚度D乘以2倍的平均曲率的积分,

因为D为常数,保持两层之间面积差不变相当于加了一个对M的约束,因此体系的自由能为

其中λ是保持A为常数的拉氏乘子,Q是保持M为常数的拉氏乘子.可见M是描述曲面形状的一个重要参数,后面将引入无量纲的约化面积差Δa来描述它.

给定自由能后,因为开口膜泡的内外渗透压为零,所以没有体积约束项.膜泡的平衡形状由自由能的一阶变分为零,即δ(1)F=0得到[25,26].

相比于SC模型,BC模型与类脂双层膜的实际情况更加符合.在BC模型的基础上,如放宽对两层之间的面积差,即认为两层之间的面积差有一最优化值ΔA0,而在形变过程中,实际的面积差可以偏离该最优化值ΔA0,但要消耗一非局域弹性能该模型称为ADE模型[27].在ADE模型下以最优化面积差ΔA0(或约化的Δa0)为参量,ΔA0是一个目前实验还无法测量的参量.

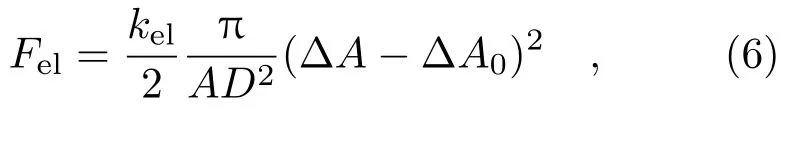
因为以上三种模型的解集是相同的,以往的计算中都是先计算BC模型的形状,再通过映射的方法得到ADE模型下的形状[27].在目前的弛豫法的计算中[15,18]简化了该过程,不借助于BC模型,而是直接给出ADE模型下的形状.但相应的计算结果以ΔA0(或约化的Δa0)为参量,而没有给出实际面积差ΔA(或约化面积差Δa)的值.目前对开口膜泡及黏附膜泡还没有在BC模型下的计算结果发表.

2.2 旋转对称膜泡参数化

对于旋转对称开口黏附膜泡,其形状可由一平面曲线绕对称轴旋转得到,图1是膜泡的参数示意图,S∈[0,S1]代表膜泡轮廓线的弧长,膜泡与黏附衬底或培养基接触边界的弧长S=S0=0,开口端的弧长S=S1;参数φ代表曲线切线与水平线的夹角;z轴为旋转对称轴;r轴与培养基的方向重合,r代表曲线上一点到旋转对称轴的距离,且满足关系式˙r=cosφ,˙z=sinφ;膜泡的黏附半径用Rcon来表示(在没有黏附的情况下,则Rcon取为零).平均曲率和高斯曲率可以相应地表示为,˙φ代表φ对弧长的导数.在此参数化表示下,文中分别给出无黏附情况下[15,17,18]及有黏附情况下[19]膜泡的Euler-Lagrange方程及其满足的边界条件,这时相应的方程是一组常微分方程组,可以通过打靶法求解给定边界条件下的相应的Euler-Lagrange方程组.

图1 开口黏附泡参数图Fig.1.Schematic picture of the adhesive opening-up vesicle.

2.3 计算方法

关于在BC模型下计算黏附膜泡的详细方法,我们将在后续的论文中详细讨论.在计算中有四个参数,总面积A、面积差ΔA、线张力系数γ和黏附系数ω.由于总能量(2)式具有标度不变性[27,28],若一个膜泡的参数方程为{r(S),z(S)},另一膜泡的参数方程为{r′(S),z′(S)},若这两个形状相似,即{r(S),z(S)}=β{r′(S),z′(S)},则总面积′,黏附面积,开口处的长度. 则只要γ=γ′/β,ω=ω′/β2,ΔA=β2ΔA′,两膜泡的能量就是相等的.因此定义膜泡的约化半径

并定义约化面积差

则两相似形状的Δa必定是相同的;并在此基础上定义无量纲的参数

3 数值计算结果

3.1 无黏附膜泡的计算结果

Umeda和Suezaki[15]研究了球形附近的开口膜泡,他们发现了两端开口的管形和烟囱形,以及一端开口的杯形解,这些形状开口处都是外凸的.他们宣称当Δa0＞1.23时没有发现开口膜泡.而我们小组发现在大的Δa0值下仍然有解,例如单开口及双开口哑铃形.其中单开口哑铃形的Δa0最大值可以取到1.725[18],那么单开口哑铃形膜泡与杯形膜泡是否是同一支解,即在参数空间中可否通过连续的参数变化从一支得到另一支,仍然是一个待解决的问题.

以往的计算是在ADE模型下进行的,即在给定优化面积差Δa0的情况下计算平衡形状,而通常得到的平衡形状的Δa值并不等于Δa0.虽然每一个平衡形状解出,它的Δa值就可知,但文献中并没有给出该值[15,18].为了与以往的结果进行比对,我们也用ADE模型进行了独立计算,并得到了文献[15,18]的所有结果,发现在其参数范围所得到的形状开口都是外凸的.以杯形膜泡为例,在不同的线张力系数下,当Δa0值增加时,开口半径都趋于0,膜泡的外形都趋于球形,发现这些形状的实际Δa值都是小于1的.我们发现该支解确实无法在参数空间中连续地趋向于单开口哑铃形状.

为了得到Δa值稍微大于1的解,我们在BC模型下进行了计算.因为在BC模型下控制的参量是Δa,这样更利于找到给定Δa值的形状.

对于一个给定的分支,Δa在一定程度上反映了膜泡的形状,在数值计算中,可以通过给定Δa来寻找相应的解,然后对Δa进行循环,就可得到这一支解中的所有形状.但由于Δa＞1与Δa＜1属于不同的分支,因此为了确定Δa＞1的分支解是否存在,必须独立寻找试验参数,并用打靶法去确定相应的解是否存在.一旦一个分支解找到后,还可以对约化线张力系数进行循环以研究形状随线张力系数的变化规律,这是以后工作中的一个任务.在本文中取约化线张力系数ˆγ=0.1.最终我们发现Δa值在1附近存在两支解,结果示于图2中.

我们发现Δa趋近于1时,Δa＜1的这一支解的开口是外凸的,而Δa＞1的这一支解的开口是内凹的,而且这两支解无法从一支连续地变到另一支.

Δa＜1时的这一支解在以往文献中被称为杯形解[15,18].随着Δa值的减小,Δa＜1的这一支解可以连续地趋向于盘形.随着Δa值的增加,这支解是从平坦的盘形逐渐变成杯形.随着Δa值的继续增加,杯形膜泡的口逐渐减小,并且开口慢慢变得外凸,最后变成接近闭合球形且开口处外凸的形状,如图2中的A3和A4所示,其中A4在开口处的放大图见图3.

而Δa＞1的这一支解是我们新发现的,它无法通过Δa＜1的外凸形解连续地改变参数得到,而必须对参数的猜测值进行扫描而独立地去寻找.随着Δa值趋向于1,该形状趋向于接近闭合球形且开口处内凹的形状,如图2中的B1所示.而且随着Δa值的增大,这一支解将连续地演变到我们小组先前发现的单开口哑铃形[18].首先,随着内凹的增多,该支解先变成自交的形状(B2),然后自交消失而演变成脖子很细的开口哑铃形(B3),然后颈部变粗(B4),又进一步变细,同时开口变小,最后演变成接近闭合哑铃形的开口很小且外凸的形状(B5).

图2 无黏附时约化总能量随Δa的变化,图中亦给出了一些典型Δa值对应的形状,其中A1(Δa=0.6),A2(Δa=0.95),A3(Δa=0.98),A4(Δa=0.9999),B1(Δa=1.05),B2(Δa=1.09),B3(Δa=1.1184),B4(Δa=1.27),B5(Δa=1.4055)Fig.2.The reduced total energy of the vesicles as a function of the reduced area difference Δa without adhesion.The f i gure also shows some typical shapes with A1(Δa=0.6),A2(Δa=0.95),A3(Δa=0.98),A4(Δa=0.9999),B1(Δa=1.05),B2(Δa=1.09),B3(Δa=1.1184),B4(Δa=1.27),B5(Δa=1.4055).

我们知道闭合球形的Δa值严格等于1.这两支开口解当Δa的值从两端趋向于1时,从外形上看都趋向于闭合球形,但仔细研究发现,它们都无法严格地趋向于球形,特别是无法通过增加或减小Δa值从一支解演变到另一支解,也就是说这两支解在泛函空间是不连续的.在图3中对Δa=1附近进行了放大,可以清晰地看到这两支解之间的间隙.

我们注意到Umeda和Suezaki[15]在计算中是从Δa＜1(对应ADE模型中的Δa0＜1.23)的这一支解,即杯形解出发进行计算的,由于这一支解无法通过参数改变连续地演变到内凹形解,因而只能得到非常趋向于球形的外凸形状,而无法得到Δa＞1的这一支内凹形解,因而也无法进一步得到开口哑铃形状.这就是他们宣称当Δa0＞1.23时没有发现开口膜泡的原因.

图3 对应图2中两支解间隔处的放大图,图中A,B两点对应的Δa值分别为0.9999和1.0015,计算得到的球形解对应的a值为1.0000Fig.3.Magnif i cation of Fig.2 in the interval part between two solutions.The Δa values corresponding to A and B are 0.9999 and 1.0015 respectively.The Δa value for the sphere solution through the calculation is 1.0000.

在这一部分的最后,我们对极细颈部的形状满足的一个关系进行验证.在以往的研究中,人们发现单组分闭合膜泡由无穷小颈部连接的两个球形的极限形状满足以下关系[28]:

其中R1和R2分别是两个球的曲率半径.该关系后来又被推广到由两个组分形成的两个区域的膜泡的情况,当在两区域交界处形成无穷小颈部时,由极小颈部连接的两区域轴对称膜泡在接近颈部处的平均曲率满足以下关系[29]:

其中C10和C20分别是两区域的自发曲率;k1c和k2c分别是两区域的弹性模量;M1ε和M2ε分别是两区域靠近颈部处的平均曲率,这里两个区域的形状并不局限于球形;σ是两区域边界处的线张力系数.最近该关系又被推广到非旋转对称的情况[30].

我们计算得到的形状B3的颈部处的半径为0.0005,是在约化线张力系数ˆγ=0.1时能得到的最细颈部的形状,由于我们研究的是开口形状,渗透压取为零,因而不能通过调整渗透压得到任意小颈部的形状.随着Δa的增大,颈部处的半径逐渐增大再减小,到B5时颈部半径又达到局域极小,为0.01792.B3和B5的颈部半径已经非常小,可以用于验证关系式(12).由于我们是在BC模型下计算的,为了得到SC模型下的值,可用以下关系[28]:

其中Q是M的拉氏乘子,参见(5)式.B3形状的颈部下面部分的平均曲率接近常数,因而比较接近球形,而颈部上面部分的形状的平均曲率并不是常数,因而并不是球形的一部分.而B5形状的上下两部分都不是球形.我们的数值结果表明,在接近颈部处,对于B3形状,M1ε+M2ε=1.110+1.168=2.278,而C0=−Q/2kc=2.278476.而对于B5形状,M1ε+M2ε=1.378+1.378=2.756,而C0=−Q/2kc=2.756871.我们发现关系式(12)还是满足得很好的.

3.2 黏附膜泡的计算结果

为了更进一步研究两支开口形状之间的关系,我们在黏附膜泡的情况下进行了计算,计算的细节将在后续的论文中详细讨论.计算黏附膜泡有两种方法:一种是给定黏附系数ω(见(2)式),计算相应的平衡形状,从而也就给出了黏附半径Rcon[19];另一种是对黏附半径加一约束,而黏附系数作为相应的拉氏乘子得出.这两种方法给出的解集是相同的.第二种方法在目前的文献中还没有人采用,我们用两种方法都进行了计算,发现第二种方法在寻找给定黏附半径的解时更有效.

为了得到黏附情况下的解,可以先从黏附半径Rcon很小的情况出发,然后逐渐增大黏附半径,因为黏附半径Rcon趋于零时,计算结果就趋向于无黏附的情况.随着黏附半径的增大,膜泡黏附面积增加,可以发现Δa在1附近仍然有两支解,一支是外凸的,而另一支为内凹的.并且这两支解之间无法连续地由一支演变到另一支.

在图4中以Rcon=0.5为例给出了黏附膜泡一些典型的Δa值及临界Δa值所对应的形状.由于下面要谈到的一个Δa值可能对应有多个解,我们用字母表示该形状处于哪一支解,及某一支解的哪一段上.为了叙述的简洁和方便,在下面的讨论中,这些字母还代表相应的Δa值.

图4 黏附半径Rcon=0.5时一些典型及临界Δa值所对应的形状Fig.4.Vesicle shapes for some typical and critical values of Δa in the case of the contact radius Rcon=0.5.

对这些形状演变的进一步分析,可以发现与无黏附的情况相比,当膜泡黏附到一个衬底上时,其解出现一个很奇异的现象,那就是在一定的区间,同一个Δa值对应有三个解,这是以往闭合膜泡中从来没有出现过的现象,在BC模型下计算闭合膜泡的相图总是连续的,也就是在BC模型中对于同一支解,一个Δa值只对应惟一一个解,另一支解的出现总是以分岔的形式.而ADE模型的相图有时是不连续的,因为BC模型对膜泡双层之间的面积差也就是Δa加了一个约束,使之必须等于Δa0,而在ADE模型下放松了该约束,允许膜泡的Δa值可以不等于Δa0,因而BC模型向ADE模型映射时,出现一对多的映射,因而能量曲线发生了折叠.

通过图5给出的能量随Δa的变化关系来表示这一现象.从图5可以看出,外凸形开口膜泡的曲线在MA(Δa=1.0112)和MB(Δa=0.9834)之间发生了折叠,分成了A,B和C三段.A段相应于盘形到MA形状(各字母代表的形状见图4)的变化,在0＜Δa＜0.9834的范围内,每一个Δa值都对应一个形状,这和图2中的情况类似.为了看清楚解的折叠行为,图5中只给出了在MA和MB之间及其附近的曲线.

首先沿着A段增加Δa值,膜泡的开口半径是逐渐减小的,例如图4中的A1和A2.到达MA时,A段结束,沿着这一段继续增大Δa值已经无法给出解,即达到了临界点MA.但可以把MA对应的一组参数代入SC模型中进行计算,通过改变C0得到新的解,再把新的解的一组参数代入BC模型中进行计算,就可以得到B段的解.这时能量曲线发生了第一次折叠.B段中随着Δa值的减小,达到临界点MB,沿着B段继续减小Δa值已经无法给出解,但可以通过不同模型下参数替换的方法得到C段解,这时曲线在MB处发生了第二次折叠,沿着C段增大Δa值,得到开口继续减小的形状,达到了第一支解在C段(即外凸形解)的极限位置CL.其中A段和C段随着Δa值的增大开口半径是逐渐减小的,与无黏附的情况相同.而B段是反常的,随着Δa值的增大,开口半径是逐渐增大的.

图5 黏附半径Rcon=0.5时,在Δa=1附近约化总能量随Δa的变化Fig.5.The energy diagram as a function of the reduced area difference Δa around Δa=1 for the adhesive open vesicles in the case of the contact radius Rcon=0.5.

图5 中亦给出了第二支解的D段.D段的开始位置是D1,小于D1时也不存在内凹形解(因此D1也是第二支解的极限位置).可见与无黏附膜泡类似,在外凸形和内凹形解之间仍然存在一个间隙.

探究组（n＝50），手术创口愈合时间（7.03±2.04）d、住院时间（11.09±2.23）d；参照组（n＝45），手术创口愈合时间（9.87±3.41）d、住院时间（15.64±3.45）d；（t＝4.983，P＝0.000；t＝7.709，P＝0.000）经组间比较显示探究组手术创口愈合时间及住院时间均显著短于参照组，差异有统计学意义（P＜0.05）。

在MB和CL之间,同一个Δa值对应了外凸形这一支的三个解,例如Δa=0.9979分别对应了图4中的A2,B1和C1三个解.而在CL和D1之间,同一个Δa值对应了外凸形这一支的两个解,在D1和MA之间,同一个Δa值对应了外凸形这一支的两个解及内凹形这一支的一个解.

沿着D段增加Δa值(见图6),在较大的范围内每一个Δa值都对应这一支的惟一解(例如图4中的D1,D2,D3).并且随着Δa值远离D1,其相应的形状亦有了较大的变化.与无黏附的情况类似,可以得到自交的形状(例如图4中的D4),这是向黏附哑铃形演化的中间形状.到达MD时,可以发现这一支解也发生了折叠.继续增大Δa值,沿着这一支已经无解,通过不同模型下参数替换的方法,我们可以得到E段(代表形状如图4中的E1),然后减小Δa值得到开口持续减小的形状,直到ME时,这一支解再次发生折叠,又得到第二支解的F段.由于E段和F段的能量差别很小,导致这两条曲线非常接近,在图6中无法显示出来,为此在图6中嵌入的插图中对ME附近进行了放大.与第一支解不同的是F段与D段不相交.F段在FL处达到了极限点,其对应的形状是一个开口极小的外凸哑铃形.

图6 黏附半径Rcon=0.5时第二支解的约化总能量随Δa的变化,插图亦给出了ME附近的放大图Fig.6.The energy diagram as a function of the reduced area difference Δa for the second branch solution of adhesive open vesicles in the case of the contact radius Rcon=0.5.The insert is the magnif i cation of the f i gure around ME.

虽然线张力系数亦会导致膜泡形状发生有趣的变化,但本文重点研究由于黏附能和无黏附能导致的两支解的不同行为,因而计算中固定了约化线张力系数ˆγ=0.1.在此情况下我们还计算了黏附半径Rcon取不同值时膜泡形状的变化规律,发现Rcon在区间[0,0.2281]取值时,随着Δa值的增大,第二支解可以从接近球形的内凹开口形状演变到不自交的单开口哑铃形.而在Rcon＞0.2281时,得到的开口哑铃形在颈部是自交的.当黏附半径较小时,这两支解和无黏附的情况是类似的,即两支解不发生折叠,而随着黏附半径的增大,两支解都会发生折叠,因而导致膜泡的相变在BC模型下是不连续的.

这是一种崭新的现象,因为以往对闭合膜泡的研究表明,在BC模型下相变是连续的(在约化体积很小时,BC模型下不同的分支解之间有可能发生不连续相变).

对开口膜泡,以往在BC模型下还没有详细的研究,但人们普遍认为在BC模型下相变是连续的.而我们在3.1节的研究表明,对本文中研究的这两支解而言,在无黏附情况下,开口膜泡在BC模型下的相变确实是连续的.而在有黏附时,开口膜泡在BC模型下会发生不连续相变,不连续相变点就在解的折叠区域.因而BC模型下的不连续相变是开口黏附膜泡才会发生的现象.

发生这种现象的原因是,考虑了黏附能后,膜泡形变的自由度增加,导致同一Δa值可以对应同一支解的几个解,因而能量曲线发生折叠,从而导致不连续相变的发生.

总结3.1节在无黏附情况下的计算表明,外凸和内凹解之间有一个间隙,在区间(0.9999,1.0015)不存在开口解.而闭合解只存在于Δa=1,对应球形.而当Δa趋于1时,外凸形及内凹形的外形很趋向于球形(如果不对开口处放大很难看出区别),但并不能严格地趋向于球形.

在本节有黏附的情况下的计算结果表明,两支开口形膜泡的间隔将向右移动,在区间(1.0039,1.0053)无开口解,区间端点分别对应图5中的CL和D1点.而且闭合膜泡不是只有Δa=1的一个球形解,而是在区间[1.0036,1.0161]都存在闭合解(图7中给出了闭合的三个典型形状).这更明确地表明外凸、内凹及闭合形状属于不同的分支解.

这里在计算闭合膜泡时研究的是对体积不加约束的情况,或渗透压为零的情况,因为开口膜泡的渗透压必为零,即只研究膜泡被打开一个孔时,膜两侧的渗透压是连续变化的情况.而以往闭合膜泡之所以会出现很多分支解[1]是因为要对膜泡同时加面积及体积约束,相当于渗透压不为零.因而与我们的计算条件是不同的.

图7 在间隙CL和D1附近约化总能量随Δa的变化,其中实线表示闭合黏附膜泡的能量,虚线表示开口黏附膜泡的能量,开口黏附膜泡两支解的间隔区间为(1.0039,1.0053)Fig.7.The reduced total energy of the vesicles as a function of the reduced area difference Δa.The solid line denotes the energy of the closed adhesive vesicles while the dash line shows that of the opening-up adhesive vesicles.The interval between two solutions of the opening-up adhesive vesicles is(1.0039,1.0053).

4 结论

本文运用打靶法研究了BC模型中轴对称开口黏附膜泡的形状转变,计算中固定约化线张力系数=0.1,得到了以下结论.

1)在无黏附的情况下,发现Δa在1附近存在两支解,Δa＜0.9999的一支是开口处外凸的解,而Δa＞1.0015的一支是开口处内凹的解.这两支解存在一个间隙,即Δa在(0.9999,1.0015)不存在开口解.这两支解不能从一支连续地演化到另一支,也不能演化为闭合的球形.

2)在有黏附的情况下,仍然发现存在类似的两支解,在固定黏附半径的系综中计算,当Rcon=0.5时,这两支解的间隙右移到(1.0039,1.0053),即在该区间无开口解.与无黏附情况在间隙附近只存在Δa=1的闭合球形不同的是,当Rcon=0.5时,在该间隙附近,Δa在区间[1.0036,1.0161]都存在闭合解.这更明确地表明,两支开口形解和闭合形解属于不同的分支解.另外一个有趣的结论是对有黏附的开口膜泡,在Δa参数空间,同一支解会发生折叠,即出现同一Δa值对应多个解(形状)的情况,这在以往BC模型的计算中是从没出现过的情况.

3)在有黏附和无黏附的情况下,间隙右侧的这一支内凹形解都会随着Δa的增大,先演化为自交的形状,然后随着Δa的进一步增大演化为开口哑铃形.而间隙左侧的外凸形开口膜泡则不会连续地演化为开口哑铃形,因而从外凸形开口膜泡无法得到开口哑铃形.这就阐明了以往文献中出现的外凸形杯形膜泡和开口哑铃形的关系.

在以往的研究中,由于线张力系数增大时,开口可以变得非常小,因而人们先验地认为开口形状可以连续地演变为闭合形状.虽然从实验角度来看,该演化可近似看成连续的,但在数学求解的角度,开口形状和闭合形状具有不同的拓扑结构,它们不能连续演化.而我们通过计算得到的内凹开口形这一支解也不能连续地演变成闭合形状,而且这两支开口解不能相互演化.只能独立去探寻发现不同的分支解,而不能通过参数的连续变化从一支得到另一支.这也说明了为什么Umeda和Suezaki[15]通过连续增大Δa0以增大Δa,并没有得到内凹形解这一事实.

给出了这些解的分支,下一步就可以系统地研究在黏附系数及线张力系数下膜泡的相变行为,并与以后可能的实验进行比较.

需要指出的是,本研究中运用的求解常微分方程的方法只能给出轴对称形式的解,而实验上发现了非旋转轴对称的稳定膜泡,这时Ouyang-Helfrich形状方程是一高阶非线性偏微分方程[25,26],目前还没有数值求解该偏微分方程的方法.对非旋转对称形状,目前只能用基于有限元的直接极小化方法进行数值计算.在本文中,我们只研究了高斯曲率弹性模量为零的情况,而高斯曲率模量对黏附膜泡的影响、多组分脂质膜泡的黏附行为、细胞与细胞之间的黏附等相关行为的研究也是十分有趣和有意义的,还有待进一步的深入研究.

[1]Seifert U 1997Adv.Phys.46 13

[2]Alberts B,Bray D,Lewis J,RaffM,Roberts K,Watson J D 1983Molecular Biology of the Cell(New York:Garlan Publishing)pp112–115

[3]Sternberg B,Grumpert J,Reinhardt G,Gawrisch K 1987Biochim.Biophys.Acta898 223

[4]Bernard A L,Guedeau-Boudeville M A,Jullien L,Meglio J M D 2000Langmuir16 6809

[5]Sackmann E 1996Science271 43

[6]Keller C A,Glasmstar K,Zhdanov V P,Kasemo B 2000Phys.Rev.Lett.84 5443

[7]Seifert U,Lipowsky R 1990Phys.Rev.A42 4768

[8]Capovilla R,Guven J 2002Phys.Rev.E66 041604

[9]Tordeux C,Fournier J B 2002Phys.Rev.E65 041912

[10]Rosso R,Virga E G 1999Proc.R.Soc.Lond.A455 4145

[11]Das S,Du Q 2008Phys.Rev.E77 011907

[12]Saitoh A,Takiguchi K,Tanaka Y,Hotani H 1998Proc.Natl.Acad.Sci.USA95 1026