脉冲放电产生螺旋流注的等离子体特性研究∗

邹丹旦 蔡智超 吴鹏 李春华 曾晗 张红丽 崔春梅

1)(华东交通大学,南昌 330013)

2)(江西省电力设计院,南昌 330096)

3)(合肥工业大学,合肥 230009)

1 引 言

近年来,高压脉冲放电方式产生低温等离子体射流作为一种新型安全的气体放电技术,由于其在材料表面清洗、杀菌消毒、癌细胞处理等方面的应用前景受到人们的广泛关注[1−4].最新研究发现,等离子体射流放电是流注放电的一种[5],其放电通道头部的电荷分离会产生局部较大的空间电场,电子在此局部空间电场的加速下,与气体分子产生发光发热的电离反应,可以通过高速摄像机捕捉到这一发光区域的传播推进过程[6].但与通常长间隙条件下的流注放电不同,研究人员发现等离子体射流放电方式所产生的非平衡等离子体具有稳定可重复的放电通道和传播特性[7−12].而如何引导及控制流注头部在放电过程中的传播发展方向成为当前研究的一个焦点[5,13].

螺旋现象及其手性问题一直广泛存在于生物DNA、单壁碳纳米管材料、复合超材料、等离子体湍流等研究领域[14−19].而目前气体放电中的螺旋研究主要集中在介质阻挡放电产生的二维螺旋波斑图方向[20,21].国外曾有研究者在直流电源驱动下通过辅助电极、外部加热及外加振动调制等人为破坏极向对称性方式产生三维螺旋的辉光放电[22].但目前还较少有关于对流注放电进行引导形成三维螺旋的研究[23].

本文采用单针电极的脉冲放电产生螺旋流注等离子体结构,通过建立电磁理论模型解释其极向电场的形成机制,并对与放电实验中螺旋手征性(左手性和右手性螺旋)相关的因素进行讨论.螺旋等离子体放电形态随放电参数的变化具有初值敏感性,并具有不同的放电模式状态,本文针对不同放电模式之间的转换过程进行讨论,通过计算推进速度、推进电场等参数对过渡模式进行分析.

2 螺旋流注放电实验

三维螺旋形等离子体放电现象及实验装置如图1所示.放电实验采用单针铜电极结构,电极直径3 mm,外部包围石英介质.电极伸入石英管内15 mm,与石英管的轴线平行.石英介质管的长度为1 m,内径为6 mm,外径为9 mm,介质管中的工作气体为氮气.

通常介质管内的单针电极放电所产生的流注都沿着管的轴向直线传播,而在特定频率的脉冲电压驱动下,实验中的等离子体自发形成了稳定的螺旋形放电通道.通过高速拍照技术捕捉到的动态过程图像证实(如图2所示),肉眼看似连续的螺旋等离子体放电通道和射流所产生的放电通道一样,都是由一个高速向前推进的发光电离体所组成,传播推进过程稳定可重复.图2中每帧图片的曝光时间为5 ns,而图中显示流注头部发光区域仍然呈螺旋形结构,螺旋的长度大于一个螺旋周期.

从实验装置上分析,电极周围并未放置破坏轴对称性的障碍物或带电体,而介质管内的等离子体却自发形成了螺旋形的电离结构,并沿着稳定可重复的通道向前推进.而且螺旋的手征性(左手性和右手性螺旋)随放电参数(如脉冲频率、接地和电压)的变化而改变.

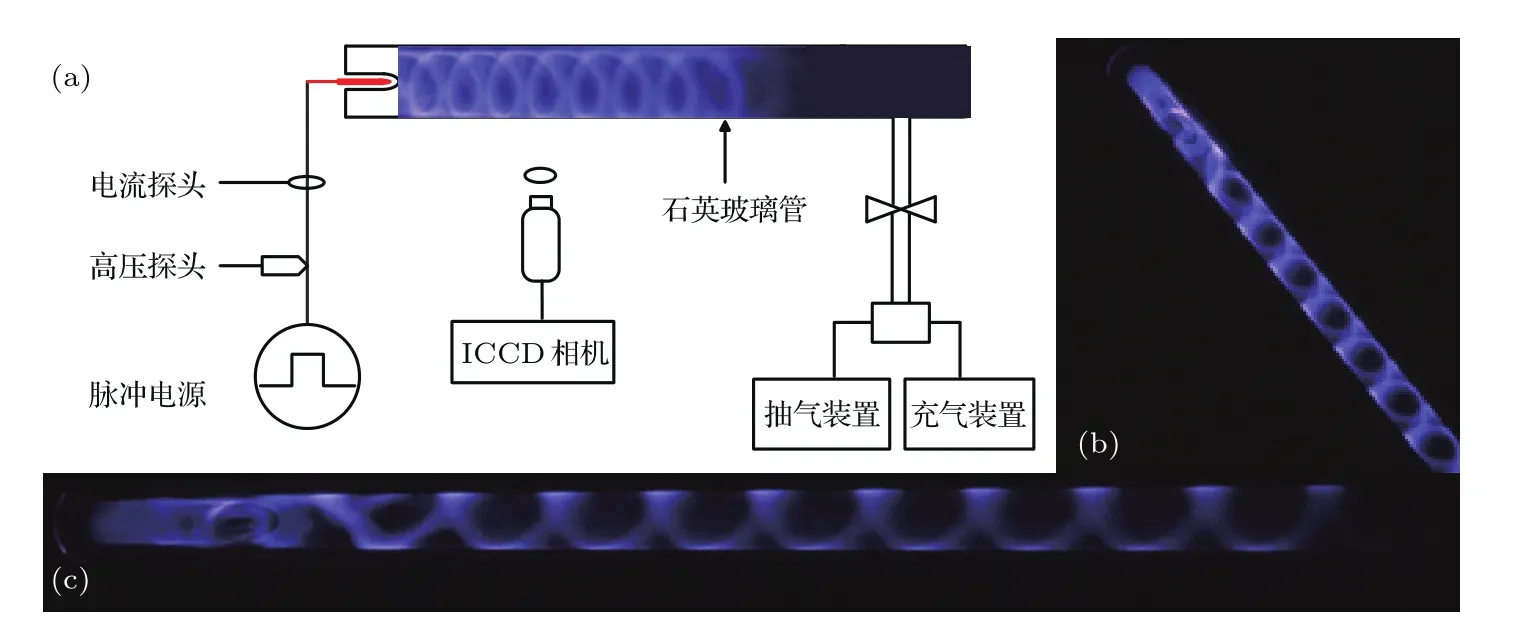
图1 (网刊彩色)(a)螺旋放电实验装置示意图;(b)螺旋等离子体斜视图;(c)螺旋等离子体轴向侧视图Fig.1.(color online)(a)Schematic of the experimental setup for helical discharge;(b)oblique view of helical plasma plume;(c)side view of helical plasma plume.

图2 高速摄像机(ICCD)拍摄下的螺旋流注传播推进动态过程Fig.2.Dynamical process of helical streamer in ICCD.

3 螺旋流注的电磁模型

为解释螺旋放电中破坏轴对称位形的极向电场来源,我们考虑电极放电所引起的电磁效应,在圆柱坐标(r,φ,z)下,先不考虑轴向电场(Ez=0),电磁场的波动方程(频域)可写为[24]

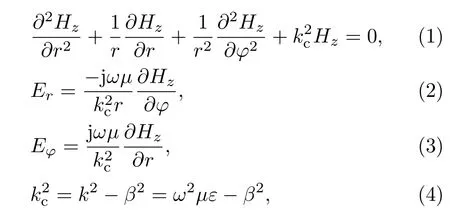
其中H为磁场强度,k为波数,β为相位常数,ε为介电常数,µ为磁导率.

设所有场量沿Z轴方向指数衰减,利用分离变量法,设

代入波动方程整理得

为使其对任意的r,φ成立,等号两边必为同一常数,即

解得

其中Jm(kcr)为第一类m阶贝塞尔函数.于是有

极向电极则为

当m=0时,

其中当r=0时,零阶贝塞尔函数的导数J′0(kcr)=0,随着r的增大,J′0(kcr)逐渐增大.从而可知其存在极向分量的电极,该极向电场在管中心处为零,而后随r逐渐增大.

极向电场Eφ的大小除了正比于零阶贝塞尔函数的导数之外,还与中心初始场强E0相关.而极向电场Eφ所取的正负号和Eφ的方向有关,并决定了螺旋的手性方向.在实验中发现,螺旋的手征特性对初值及边值条件具有明显的敏感性,其中接地引起的介质管电势边值条件变化也对螺旋流注的手性特征及形态具有一定影响.图3所示为介质管中端接地后,螺旋流注传播通道在接地点两侧发生的手征性变化.实验表明螺旋放电形态的出现与介质管壁表面的电场分布有着重要关系.因而形成螺旋流注所需的沿电极轴向的电场分量可以由轴对称的外加电极电场提供,而破坏轴对称的极向电场来源需要用电磁理论机制来解释.

图3 (网刊彩色)螺旋放电通道在介质管接地点两侧的手征性变化Fig.3.(color online)The chiral characteristic of helical discharge channel affected by electrical grounding of dielectric tube.

4 放电模式转换研究

通过实验研究发现,流注的螺旋放电模式与沿管径直线放电模式之间还存在着过渡过程.在过渡模式中,等离子体形态会敏感地随电源的脉冲重复频率等放电参数的变化而改变.为了讨论螺旋放电与直线型放电两种模式的相互转化过程,我们将电极电压固定在6 kV,脉宽固定在3µs,气压固定在4 kPa,选择拍摄了700,1400,3000 Hz三种放电频率.如图4所示,当频率为700 Hz时,放电形式为沿管壁的螺旋放电;当频率增大到1400 Hz时,出现了一种介于全螺旋放电与沿管中心直线放电之间的过渡放电模式,在该模式下,电极附近以螺旋形式放电,而后转入直线形式的放电,在尾端再次转为螺旋放电;当频率增大到3000 Hz时,放电完全转化为沿管中心的直线放电.

与图4(b)中过渡状态对应的放电动态过程如图5.

图4 (网刊彩色)通过调整脉冲频率得到的三种不同形式的放电模式Fig.4.(color online)Three type of discharge modes acquired by different pulse frequency.

图5 脉冲重复频率为1400 Hz时ICCD拍摄的螺旋放电动态过程Fig.5.Dynamical process of helical discharge with pulse frequency of 1400 Hz in ICCD.

对应于脉冲重复频率为1400 Hz的动态过程未能抓拍到电极附近螺旋的转变过程,这是因为该过程发生的时间尺度较快,一般都在300 ns以内.而在300 ns的时间间隔内,可以清楚地看到流注头部传播一定距离后即开始向螺旋转变.我们发现当放电模式转换为螺旋放电时,流注头部不仅亮度变暗,发光区域变小,形状发生弯曲,而且传播速度明显变慢.计算表明,此时螺旋流注的传播速度都处于104m/s量级.

对应于放电频率为3000 Hz的动态过程,放电形式完全转化为沿管中心的直线放电形式,与通常的流注传播过程没有区别.从以上ICCD动态过程整理得到的流注传播推进速度如图6所示.

图6 流注传播速度随时间的变化Fig.6.The relationship between propagating velocity of streamer and time.

在氮气中,电子迁移率与压强有如下经验公式:µep=0.42×106.因此在气压为4 kPa时,电子迁移率为µe=1.4×104cm2/(V·s).假设漂移速度与流注传播速度相当,轴向电场可以通过以下关系估计:Ez=vd/µe.在完全螺旋放电时(频率700 Hz),对应于图6中915 ns时3×104m/s的传播速度,可以估算轴向电场处于2×104V/m量级.对于完全螺旋放电时极向电场的估算,可以假设螺旋流注沿介质管内壁面传播(介质管内管直径为6 mm,周长为6 mm),而图2的动态过程图像显示,615—915 ns时间间隔内流注正好传播了一个螺旋周期.以介质管的周长为路程,300 ns为传播时间,可以估算出流注在极向的传播速度约为2×104m/s,而极向电场也处于104V/m量级.此时极向与轴向的传播速度(及电场)的量级相同,两者的比值约为0.67.电磁模型在(13)式中所得到的单一波模的极向电场表达式中,如果设介质管轴心处的初始电场E0为轴向电场,在电极附近极向电场Eφ与E0的比值为零阶贝塞尔函数的导数J′0(kcr).而在介质管边缘,J′0(kcr)的绝对值取最大值时可以达到0.58,与通过动态过程图像估算的比值相近.

而改变脉冲电源的重复频率,使脉冲频率由700 Hz升高到1400 Hz时,脉冲电源在介质管内所辐射电磁波的频率分量发生了变化.当这些频率分量接近于介质管中的两种本征波模时,会使得这两种本征波模同时增长并发生相互作用和干扰.当两种不同频率和波长的波模叠加后,其共同形成的极向电场将在轴向的不同空间位置处发生相应的增长和抵消.当叠加后的极向电场与该处的轴向电场相近时,流注在该空间位置处沿螺旋放电通道传播;而当叠加后的极向电场远小于该空间位置处的轴向电场时,极向电场Eφ与轴向电场的比值趋近于零,流注沿极向的圆周运动可以忽略,放电回归到沿管中心的直线放电模式,从而在这种混合波模下出现了过渡放电模式.由于混合波模的计算中涉及复杂的波-波相互作用,我们将在以后的数值仿真研究工作中展开更深入的探讨.

5 结 论

1)在没有外加恒定磁场的情况下,通过脉冲放电发现一种螺旋形态的流注放电现象.这种螺旋流注放电可以形成稳定可重复的放电通道.通过动态过程图像发现,流注的头部也呈螺旋形态.

2)螺旋流注可以呈现左手性和右手性两种不同的手征特性.

3)通过电磁理论机制解释了破坏轴对称的极向电场来源.从电磁波动方程出发,得到忽略等离子体响应简化后的波模.在该模式下,极向电场满足零阶贝塞尔函数的导数形式.由零阶贝塞尔函数导数的性质可知,存在极向分量的电场,该极向电场在管中心处为零,而后随管径的增大而逐渐增大,与实验中螺旋流注沿管壁附近传播的现象一致.

4)通过流注传播推进速度,估算了其传播所需的轴向和极向电场.估算的两者比值与之前电磁单一波模计算得到的极向与轴向电场比值相近.

[1]Zhang Y C,Yang K,Li H,Zhu X D 2016Acta Phys.Sin.65 145201(in Chinese)[张一川,杨宽,李唤,朱晓东2016物理学报65 145201]

[2]Li X C,Li Y R,Zhang P P,Jia P Y,Dong L F 2016Sci.Rep.6 35653

[3]Jin Y,Qian M Y,Ren C S,Wang D Z 2012High Voltage Eng.38 7(in Chinese)[金英,钱沐扬,任春生,王德真2012高电压技术38 7]

[4]Shi X M,Zhang G J,Wu X L,Li Y X,Ma Y,Shao X J 2011IEEE Trans.Plasma Sci.39 1591

[5]Lu X P,Naidis G V,Laroussi M,Ostrikov K 2014Phy.Rep.540 123

[6]Teschke M,Kedziersk J,Finantu-Dinu E G,Korzec D,Engemann J 2005IEEE Trans.Plasma Sci.33 310

[7]Li S Z,Huang W T,Wang D Z 2009Phys.Plasmas16 093501

[8]Fridman G 2008Plasma Proc.Polym.5 503

[9]Mor fi ll G 2009New J.Phys.11 115011

[10]Huang J,Li H,Chen W,Lü G H,Wang X Q,Zhang G P,Ostrikov K,Wang P Y,Yang S Z 2011Appl.Phys.Lett.99 253701

[11]Lu Y,Wang L Y,Ma K,Li G,Zhang C,Zhao H X,Lai Q H,Li H P,Xing X H 2011Biochem.Eng.55 17

[12]Xu L,Liu P,Zhan R J,Wen X H,Ding L L,Nagatsu M 2006Thin Solid Films506–507 400

[13]Liu L J,Zhang Y,Tian W J,Meng Y,Ouyang J T 2014Appl.Phys.Lett.104 244108

[14]Snir Y,Kamien R D 2005Science307 1067

[15]Tans S J,Devoret M H,Dai H J,Thess A,Smalley R E,Geerligs L J,Dekker C 1997Nature386 474

[16]Wang Z K,Yang Z Y,Tao H,Zhao M 2016Acta Phys.Sin.65 217802(in Chinese)[汪肇坤,杨振宇,陶欢,赵茗2016物理学报65 217802]

[17]Matthaeus W H,Goldstein M L 1982Phys.Rev.Lett.48 1256

[18]Pan F,Wang X Y,Wang P,Li W X,Tang G N 2016Acta Phys.Sin.65 198201(in Chinese)[潘飞,王小艳,汪芃,黎维新,唐国宁2016物理学报65 198201]

[19]Zeng Y H,Jiang W G,Qin Q H 2016Acta Phys.Sin.65 148802(in Chinese)[曾永辉,江五贵,Qin Qing-Hua 2016物理学报65 148802]

[20]Wang H F,Dong L F,Liu F C,Liu S H,Liu W L 2007J.Heibei Univ.(Nat.Sci.Ed.)27 475(in Chinese)[王红芳,董丽芳,刘富成,刘书华,刘微粒2007河北大学学报27 475]

[21]Bai Z G,Li X Z,Li Y,Zhao K 2014Acta Phys.Sin.63 228201(in Chinese)[白占国,李新政,李燕,赵昆 2014物理学报63 228201]

[22]Strumpel C,Astrov Yu A,Ammelt E,Purwins H G 2000Phys.Rev.E61 4899

[23]Zou D D,Cao X,Lu X P,Ostrikov K 2015Phys.Plasmas22 103517

[24]Lieberman M,Booth J,Chabert P,Rax J,Turner M 2002Plasma Sources Sci.Technol.11 283