颗粒样品形变对声波传播影响的实验探究∗

2017-04-26周志刚1宗谨1王文广1厚美瑛1

物理学报 2017年15期

关键词：声速声波轴向

周志刚1)2) 宗谨1)3) 王文广1)2) 厚美瑛1)2)

1)(中国科学院物理研究所,软物质重点实验室,北京凝聚态物理国家重点实验室,北京 100190)

2)(中国科学院大学物理科学学院,北京 100049)

3)(西北师范大学物理电子与工程学院,兰州 730070)

1 引言

颗粒固体在自然界和工业生产中是很常见的颗粒物质的聚集状态,如沙堆、谷堆,它是由许多离散的固体小颗粒所组成的体系,只有相邻的颗粒间才存在相互的摩擦和压力.由于颗粒间接触点的分布是随机方向的,颗粒固体体系内所形成的接触网络非常复杂,并且外界小的扰动,都能导致颗粒固体体系中接触网络和力链结构的变化[1−3].颗粒固体体系能表现出类似于通常弹性固体的性质,如有确定的堆积形态,但又与通常弹性固体很不同;在一定的外力作用下,通常的弹性固体发生的宏观形变与组成弹性固体每一部分的形变满足线性关系,为仿射形变;但颗粒固体体系的形变往往是由局部颗粒位置的变化所导致的,是一种非仿射形变[4].

由于透过颗粒体系的声波能反映颗粒体系内部结构和力的信息,并且幅度很小的超声波在透过颗粒物质时往往不对其结构产生破坏[5,6],是研究三维颗粒物质体系内部结构和力的一种手段.如直剪实验中,探测颗粒介质中剪切波声速的变化,可以判断样品中是否形成了剪切带[7−9].有效介质理论(EMT)通常被用来描述声波在颗粒介质中的规律,其预言了颗粒样品的模量,在许多实验中,发现体变模量(K)随压力的关系是满足EMT的,然而剪切模量(µ)无论是大小还是变化趋势都偏离EMT的预测[10,11].Makse等[4]指出颗粒固体体系在外界压力的作用下,体系的接触网络和平均配位数都将变化,仿射近似对颗粒固体体系不严格成立.他们对EMT进行配位数的修正后,剪切模量的理论值和实验测量值定性地符合.

在颗粒物质的单轴实验中,当样品受到轴向压力时,体系中的颗粒不仅会沿轴向运动,还可能偏离于轴向发生滑动,填补周围的空隙,颗粒的这种非仿射运动在宏观上对应于颗粒固体体系的轴向形变;这个过程虽然不像文献[8,9]中剪切带的形成那样颗粒的接触网络发生剧烈的变化,但相比于加载前,颗粒间的接触情况是变化的,颗粒的平均配位数会有所增加[4].而声波在颗粒体系中是通过颗粒间的接触传播的,所以这个过程应该会对声波在颗粒介质中的传播产生影响.本文主要是通过实验探讨外界压力引起的颗粒体系内部接触结构的变化(宏观对应于样品发生的形变)对声波传播的影响.具体而言就是在样品轴向上施加一系列逐渐增大的力,样品宏观上对应产生一系列逐渐增大的形变,讨论这种形变所对应的颗粒间接触结构的变化对颗粒体系中声波传播的影响.我们发现在这个过程中,声波波形的非相干部分不断变化,声速在样品发生形变的起始阶段明显偏离EMT的预测.

2 实验

实验中所用的颗粒为干燥玻璃珠,粒径分布约为0.28≤d≤0.44 mm;玻璃珠通过漏斗注入直径为51.0 mm的圆柱形金属容器中,样品高度H=63.5 mm,体积分数ϕ约为61%;在圆柱容器的顶部和底部分别放置着发射和接受超声波的超声压头,其中心频率为80 kHz,直径为50.5 mm,超声压头与圆柱形容器内壁大小符合,无颗粒漏出.图1为实验装置示意图,左上角为超声压头示意,黑色突出部分为产生剪切波的弯曲单元.由于压电晶体和颗粒样品不是直接接触的,声波在通过压头表面的金属保护层时会发生散射和损耗,最后实际进入颗粒样品中声波的中心频率往往小于80 kHz.按照实验中测得的声波的速度(约400 m/s)和频率(约30 kHz),可估测此压头产生的声波在样品中的有效波长λeff=υeff/f≈13 mm,远大于实验中所用颗粒的直径,声波是能较好地透过颗粒样品的.实验中样品轴向上的形变量由线性差动变压器(linear variable differential transformer)测量,实验的环境温度和湿度分别为23°C和30%.

图1 (网刊彩色)实验装置示意图Fig.1.(color online)Experimental sketch.

为了使颗粒样品产生不同的形变,在实验中具体采用的加载过程如图2:轴向压力由20 kPa增加到50 kPa,停留2 min,回到20 kPa,然后增加到100 kPa,停留2 min,再回到20 kPa;如此进行下去,直到轴向加载达到900 kPa后,再回到20 kPa.为了后面说明的方便,将一系列压缩颗粒样品产生不同形变的压力记为压缩压力(Pcomp),将返回的同一压力20 kPa进行测量时的压力,记为观察压力(Pobse).样品由Pcomp返回Pobse时,部分形变不可恢复,我们则是要测量在Pobse下,这些由Pcomp产生的形变对颗粒体系中声波传播的影响.

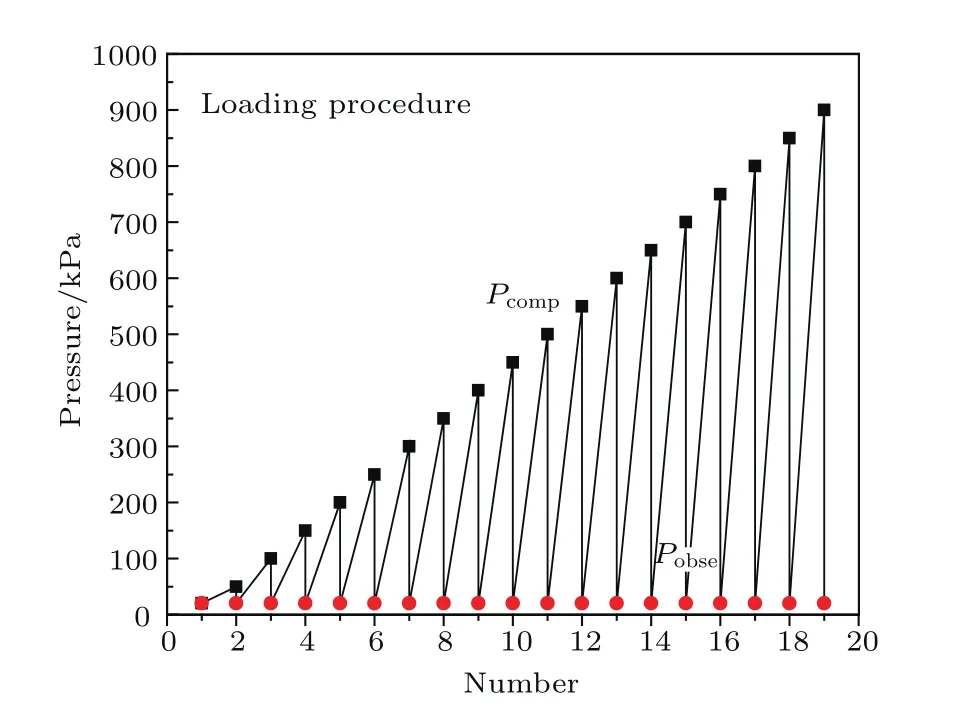
图2 (网刊彩色)加载过程Fig.2.(color online)Loading procedures.

3 实验结果与讨论

首先我们来看加载过程中样品形变量的变化.如图3,轴向力作用于装在刚性边壁容器中的颗粒体系,颗粒样品只允许在轴向上被压缩,径向不发生形变;样品在Pcomp下的形变ε,包括弹性部分εe(主要是颗粒间的弹性形变的宏观总和)和塑性部分εpl(主要是颗粒发生滑动导致的);随着施加到样品上Pcomp的增加,轴向发生的形变几乎是线性增大(斜率其实是在渐渐减小的),返回到Pobse时,样品的轴向形变有所恢复,最后不可恢复的形变也是随Pcomp的增大而增大.实验中加载的轴向外力最大为900 kPa,远远小于玻璃的剪切模量,可不考虑这个过程中的颗粒破碎的问题.整个实验过程中,样品在Pcomp下的最大形变为1.286 mm,此时样品的体积分数增加2.03%;返回到Pobse时,样品轴向最大形变量为0.905 mm,样品体积分数变化1.43%.

当Pcomp作用于样品时,在颗粒层面上,样品中的颗粒并不是都沿轴向上发生微小移动,颗粒会向其周围的空隙移动,使样品变得更加密实,颗粒的这种重排过程和样品轴向形变不满足仿射关系,是非仿射运动,这个过程中颗粒的平均配位数有所增加,体系内的接触结构也将发生变化[3,12].返回Pobse时,残留下的应变对应为非仿射应变.下面我们先介绍通过形变量不断增加的颗粒体系后声波波形的变化特点.

图3 (网刊彩色)不同压力下颗粒样品轴向形变量Fig.3.(color online)Axial deformation of the granular simple under different stresses.

3.1 波形变化

图4 给出了样品经过Pcomp=20,300,600,900 kPa压缩后返回Pobse时通过样品的声波波形图,在这些压力作用下样品轴向分别发生了0,0.338,0.63,0.905 mm的形变,通过这些在颗粒接触结构上发生不同程度变化的颗粒样品后的声波,存在相似的较为稳定的首波(一个到几个波长左右)[13,14],这是通过样品后最快到达接收压头的波,称为相干波;紧跟相干波后长度有几百微秒的是非相干波.如图4,通过不同压缩量样品的非相干波是有差别的,并且这种差别随着样品形变量的增加而变化,这和非相干波对样品中颗粒间的接触结构敏感相关,因此非相干波也可被看作是颗粒样品结构变化的指纹[15,16].

为了定量讨论非相干波波形随样品形变量增加时发生的变化,我们引入描述两列波相似程度的系数,其中,为波列的时间长度.当相似度系数越接近1时,两列波的相似度越高[5].我们计算了在Pobse下(共19列波)第1个波分别和第i个波波形的相似度系数(i为1到19的自然数),记为R(1,i);也计算了相邻两次波形的相似度系数,记为R(i,i+1).如图5所示,R(1,i)随着样品形变量的增加而不断减小,这个过程中颗粒样品内部结构相对于初始状态变化越来越大,导致通过样品的声波波形变化也越大.R(i,i+1)在样品发生形变的初始阶段较小,当轴向形变超过0.2 mm后,相似度系数都在0.8以上,这表明在样品压缩的初始阶段相邻两次压缩下样品的结构变化导致声波波形的变化比之后要剧烈,但压缩量为0.2 mm之后通过样品的声波的波形也是在不断发生变化,只是相连两次压缩导致颗粒体系结构的变化没有开始时的大.为了说明这一点,我们又分别计算了R(3,i)和R(7,i)作为比较,从曲线的变化可以看出,第3个波(对应于样品在Pcomp=100 kPa压缩后返回Pobse测量的波)和之后的波的差别越来越大,同样第7个波和后面的差别也越来越大,只是相对于R(3,i)的结果这种差别要小些.这些结果表明随着颗粒样品轴向压缩量的增加,颗粒间接触结构发生变化时,通过样品的声波波形也将发生变化,非相干波波形的变化反映了颗粒体系内部结构的变化.

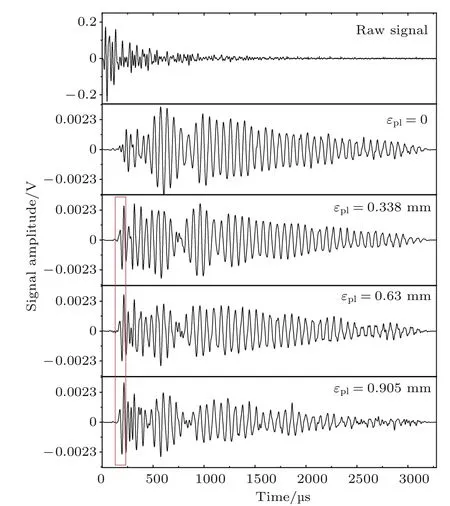
图4 (网刊彩色)通过不同形变量的颗粒样品中的声波波形图Fig.4.(color online)Sound waveforms in granular sample of different deformations.

由于使样品结构变化的Pcomp并不足够大,并且由于粮仓效应还会导致部分轴向力通过颗粒传递到容器边壁而被分担[17,18],从而对容器底部的颗粒发生结构重排的影响很弱,所以在Pobse下,颗粒样品轴向形变最大只有0.905 mm,怎样让颗粒体系结构发生更广泛和均匀的变化,这将在后面的实验中改进方案.采用振动的方式,使整个样品全局性地发生结构重排列.

图5 (网刊彩色)不同轴向形变量下声波波形的相似度系数Fig.5.(color online)Resemblance Parameters of sound waveform for different axial deformations.

3.2 声波频率和能量的变化

由于颗粒介质体系是由散体的颗粒组成,颗粒的配位数的随机性导致颗粒体系内部的接触结构很复杂,相互间的接触力随颗粒形变的关系也并非简单的线性,这些将使声波在颗粒体系中的传播表现得很复杂.从颗粒层面看,当声波在颗粒间传播时,在颗粒的接触处将发生散射和耗散,并且不同的频率成分间的散射是相互独立的[19].

图6给出了接收声波信号的频率谱.首先相对于原始声波频率谱,声波在通过颗粒样品后,不同频率成分都发生了衰减,20—30 kHz间的频率成分几乎消失,但含量并不为0,波形图中的较稳定的相干波部分对应的频率成分就出现在这样的地方,并且相干波是由多种频率成分所组成的[14].频率分布于30—60 kHz的成分衰减程度也很大;声波频率的衰减来自于颗粒体系的接触结构上的各向异性和复杂性,使得其像高频滤波器一样,会很大程度地衰减高频波.具体来说声波在颗粒接触处的散射强度正比于f2,高频波在传播过程中将较快地衰减[15],只有f≪υeff/d的频率成分的声波容易通过.

图6 (网刊彩色)声波频率谱,其中,虚线为初始声波的频率谱,不同颜色的实线为发生不同应变的样品中的频率谱Fig.6.(color online)Frequency spectra of sound wave:the dash line is the frequency spectrum of initial sound wave,and the different color solid lines correspond to the frequency spectra in different specimen strains.

从图6可以看出,随着样品轴向被压缩,通过颗粒样品的声波频率谱中最高峰的位置都分布在14—15 kHz间,最高峰的大小和最高峰附近的次高峰都随样品形变量的不同而变化.在初始波的频率谱中也有一个峰值位于这个频率区间,这个频率区间的声波相对容易通过压力为Pobse下的颗粒介质体系.进行快速傅里叶变换会发现,这个频率区间在声波波形图中并不是对应较为稳定的相干波.

由于通过不同形变量样品的声波频率最高峰分布的位置较为稳定,都在14—15 kHz间,此频率段的声波占整个声波中很大部分,并且随着样品形变量的增加而变化,它反映了声波受样品散射和耗散的重要信息.我们给出了最高峰随样品形变量的变化,如图7所示.从图7可见发现最高峰并不是随着样品变密集而单调地变化,并且和通过样品的声波能量随样品形变量变化的图在形状上非常相似,这里声波能量按照|计算.这种相似性可以从频率谱和波形的关系理解,由于频率最高峰反映该频率范围的成分在频率谱中的占比,在波形图中该频率范围的波很多,并且这些波的幅值并不小,所以实验结果中频率最高峰对应的声波能量其实可反映整个声波的能量.这也表明了声波在通过颗粒的接触点发生散射的同时,声波能量在接触处也将耗散;由于声波在均匀的空气中是不发生散射的,所以这个结果也间接表明了样品中的空气对声波能量的耗散相对于在接触点上的耗散可以忽略[13,15],否则声波的能量变化曲线中若计入空气耗散的部分,其形状就和频率最高峰的变化曲线不同.总之,颗粒物质体系对于通过其中的高频声波有很强的过滤作用,很多高频部分的频率成分被散射而向低频移动或是几乎消失,颗粒间的空隙空气对声波能量的耗散远小于在颗粒的接触点处耗散.

图7 (网刊彩色)声波的频率最高峰和能量随样品形变量的变化Fig.7.(color online)The changes of the maximum frequency peak and sound energy with the sample deformation.

3.3 声波速度

前面讨论过相干波波形在样品渐渐形变过程是比较稳定的,只有非相干波在不断地变化,相干波的这种特点被用来确定声波通过颗粒介质的速度.测量出相干波的到达时间ttof和样品的高度,则声速υ=H/ttof.在土力工程中也通常用共振等方法确定声波速度.实验中我们取相干波波峰作为声波到达点,在很多文献中取波峰的3%或更小[8,9].这里之所以取波峰一方面是因为声波都是在较小的观察压力(20 kPa)下测量得到的,波形中的杂波较多,而相干波的波峰明显容易辨识;另一方面我们在实验前已标定过两超声压头直接相连时相干波波峰的时间,在计算样品中的声速时,只要减去标定的时间,即可以很大程度地减小选取波峰为声波到达点所带来的偏差.

图8所示为声速随样品形变量的变化;随着样品被压缩,声波速度最开始很快地增加,之后增加变得很缓慢,几乎趋于稳定.实验中声速的计算值已考虑了样品高度变化对声速的修正.样品最开始发生形变时的声速比之后的声速小了近60 m/s,这种偏差应不仅仅是样品的高度修正能弥补的(实验中样品高度变化带来的最大修正只有),我们认为这种差别只可能是样品初始形变阶段颗粒接触结构的变化带来的.

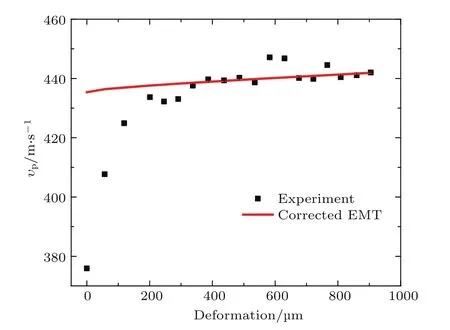
图8 (网刊彩色)声速随样品形变量的变化Fig.8.(color online)The variation of sound velocity versus the sample deformation.

样品轴向形变的不断增加对应颗粒体系变得越来越密集,颗粒的平均配位数将增加.EMT通常被用来描述颗粒介质体系中声速和压力的关系,但其严格成立的条件是组成颗粒体系的颗粒相同,并且颗粒的配位数相同;颗粒的运动和样品的形变满足仿射关系.由于没有考虑颗粒样品在压力下平均配位数将发生变化(对应于颗粒体系接触结构的变化)的实际情况,EMT在描述样品剪切模量和声速随压力的变化时出现了偏差.Maske等[4,20]在EMT中考虑了配位数的变化后,发现理论计算的剪切模量和实验定性地符合.在我们的实验中由于Pobse=20 kPa是恒定不变的,声速的变化主要是由于颗粒的非仿射运动引起的颗粒接触结构的变化导致的,图8的计算中也考虑了配位数的修正[21],,按照EMT[4,20,22]:

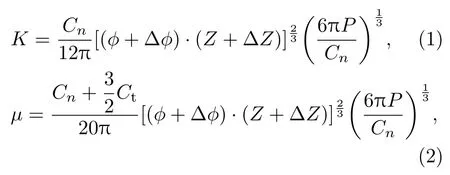
本实验中制备的样品是相对较为松散的,在不断压缩变密实的过程中,颗粒的运动将导致颗粒体系接触结构发生变化.最近有二维光弹实验[23]表明颗粒体系的接触结构不同时,颗粒间的作用力随颗粒间的形变量的关系是不同的,不总是按Hertz接触理论的3/2次关系,这很可能是导致声速随压力的指数偏离EMT的预测.本实验中三维玻璃颗粒体系受轴向压力导致颗粒体系内部接触结构的变化虽然不能像二维光弹实验那样可以直接观察,但也观察到在样品应变初始阶段的声速偏离EMT的预测,这也许与之前很多实验结果[4,13,23−25]报道的声速随压力的指数偏离1/6密切相关.

4 结论

本文通过实验探讨了颗粒样品轴向形变不断增加时对声波传播的影响,结果表明声波在通过颗粒介质时频率很快地衰减,频率谱中的最高峰的变化趋势和通过样品中声波的能量变化趋势相似.随着样品轴向形变的不断增加,通过颗粒样品的非相干波部分波形的关联系数是变化的,这反映了颗粒体系内部接触结构的变化;在这种变化的起始阶段声速较大地偏离EMT的预测;随着样品被压密,声速渐渐趋于稳定并且在实验误差范围内符合EMT的预测,这对长期争论的声速随压力变化指数偏离EMT预测的原因有所启示.

[1]Liu C H,Nagel S R,Schecter D A,Coppersmith S N,Majumdar S,Narayan O,Witten T A 1995Science269 513

[2]Jacco H S,Thijs J H V,van Martin H,van Wim S 2004Phys.Rev.Lett.92 054302

[3]Bi D P,Zhang J,Chakraborty B,Behringer R P 2011Nature480 355

[4]Makse H A,Gland N,Johnson D L,Schwartz L M 1999Phys.Rev.Lett.83 5070

[5]Tournat V,Gusev V E 2009Phys.Rev.E80 011306

[6]Jia X,Brunet Th,Laurent J 2011Phys.Rev.E84 020301

[7]Caroli C,Velický B 2003Phys.Rev.E67 061301

[8]Khidas Y,Jia X P 2012Phys.Rev.E85 051302

[9]Zhang Q,Li Y C,Hou M Y,Jiang Y M,Liu M 2012Phys.Rev.E85 031306

[10]Domentico S N 1977Geophysics42 1339

[11]Yin H 1993Ph.D.Dissertation(Stanford:Stanford University)

[12]Majmudar T S,Sperl M,Luding S,Behringer R P 2007Phys.Rev.Lett.98 058001