基于非球形雨衰模型的微波链路雨强反演方法∗

宋堃 高太长 刘西川 印敏 薛杨

(国防科技大学气象海洋学院,南京 211101)

Song Kun Gao Tai-Chang†Liu Xi-Chuan Yin Min Xue Yang

(College of Meteorology and Oceanography,National University of Defense Technology,Nanjing 211101,China)

1 引 言

降雨是十分重要的物理现象,实时准确地测量降雨对于人民生活、社会生产、部队保障和国家安全具有十分重要的意义[1].目前,在气象观测业务中测量降雨的手段主要有雨量计、天气雷达和气象卫星[2−4],地面雨量计能够较为准确地测量地表降雨强度,然而其空间代表性较差,无法监测降雨的精细分布;天气雷达虽能提供时空分辨率高的雨强数据,但受雷达扫描方式和Z-R关系不确定性(Z为测雨雷达反射率,R为降雨强度)的制约,其测量结果与地表真实降雨存在一定差异;气象卫星可自上而下测量云顶或穿透云顶,但其探测目标仍不是地表降雨,测雨精度仍有待提高.现阶段,实时准确地测量地表降水仍然存在一定的难度.

近些年,气象学者提出利用目前广泛存在的微波链路通信信号传输过程中的衰减信息反演地表降雨强度的设想,并已开展了大量的实验研究,取得了一定的进展.2006年,Messer等[5]提出利用商用微波链路探测降雨的设想,并提出了基于雨强-微波衰减幂律关系的雨衰反演模型.2008年,Feng等[6]利用启发式分割算法(brief l y BG algorithm)对中国南北方的降雨时序突变开展研究,在此基础上分析了不同地区的降雨幂律衰减特性.2009年,Goldshtein等[7]开展了不同频段商用微波链路降雨测量的实验,验证了多频段微波雨强反演的可行性.2012年,Messer等[8]提出了利用微波链路探测雪、冰水混合物等其他相态降水的设想,并提出了相关的反演模型.2013年,David等[9]进行了不同频段微波链路测雨实验,通过与实际地表降雨进行比对,验证了微波链路测雨的准确性与可行性;同年,Overeem等[10]利用超过2400条微波链路对荷兰全境进行了多频段蜂窝无线网络实时监测降雨的试验,验证了基于组网微波链路进行区域雨强反演的可行性.目前,国内在微波测雨方面研究较少,刘西川等[11,12]研究了降雨粒子对不同波段微波传输特性的影响特性,提高了复杂降雨条件下微波传输衰减的评估精度,并建立了考虑温度的降水衰减模型;2013年,姜世泰等[13]研究了基于微波链路的区域降雨反演方法,并进行了仿真研究;2015年,印敏等[14]设计了视距微波通信链路系统,并验证了利用微波链路开展实时测量降雨的可行性;同年,高太长等[15]提出了基于实地雨滴谱分布的微波链路路径雨强反演算法,并开展了15—20 GHz频段的微波链路测量实验,验证了该方法的有效性.

目前,国内外对微波链路雨强反演模型普遍采用由国际电信联盟(ITU)推荐的雨衰幂律模型,该模型是基于数据统计和通信原理建立起的经验模型[16],其形式为

式中,A(dB/km)代表微波传输雨致衰减,R(mm/h)代表降雨强度,a和b为雨衰幂律系数.对(1)式进行如下变形即可反解得到降雨强度:

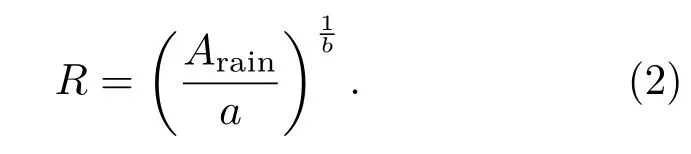
幂律系数a,b与雨滴形状、雨滴谱分布等因素有关,为了得到具有实地谱分布的幂律系数,本文利用Pruppacher-Beard(PB)降雨粒子模型[17]和T矩阵理论[18]计算非球形粒子消光截面,结合OTT雨滴谱仪记录的南京地区Gamma谱参数历史数据计算得到不同频率下微波的雨致衰减,对微波雨致衰减及其对应的降雨强度进行(1)式形式的非线性拟合,拟合得到不同频率下非球形雨衰模型幂律系数.为验证非球形雨衰模型反演降水强度的精度,开展15—20 GHz频段微波反演降雨强度的实验进行检验.

2 基于非球形雨衰模型的微波链路雨强反演模型

2.1 微波链路雨强反演原理

微波在空气中传播时会受到其中的气体、降水等因素的影响而发生吸收、衰减、散射等能量衰减现象,其中降水是主要影响因素.微波雨致衰减主要取决于降雨强度、降雨粒子形状、雨滴尺度分布等因素.基于此,根据微波雨致衰减的大小可以反演实际降雨强度.

本文基于T矩阵理论和PB降雨粒子模型,采用与我国大部分地区降雨尺度分布更为相近的Gamma谱分布[19−21],利用OTT雨滴谱仪实测的历史降雨数据进行非线性拟合,建立微波链路雨强反演模型;同时通过测量微波链路发射端与接收端的接收电平差值得到微波路径传输总衰减,根据特征大气衰减模型修正非降雨因素导致的微波传输衰减,从而计算得到链路上的微波雨致衰减Arain;通过反演模型和微波雨致衰减就可反演得到实际降雨强度.具体反演流程如图1所示.

图1 雨衰反演流程图Fig.1.Flow chart of the rainfall inversion model.

2.2 微波链路实测雨致衰减值提取

微波路径传输总衰减可表示为[22]

式中,A为微波路径传输总衰减,f为微波发射频率(GHz),D为微波传输总距离(km),Awater为水汽造成的微波传输衰减,Afog为雾或轻雾造成的微波衰减,AO2为氧气造成的微波衰减,Aair为其他气体吸收造成的衰减,Arain为降水造成的微波衰减.其中,降雨造成的衰减是微波传输的最主要衰减因素.

为提取出微波传输雨致衰减,本文在晴空条件下测得微波路径传输衰减基值,设基值为降雨时实测得到微波链路路径传输总衰减Atot.由于降雨现象发生时,大气中的温度、气压、湿度等条件和测量晴空基值时的条件会发生变化,因此要对传输衰减进行温度、气压及湿度的修正,根据降雨前和降雨时的温度、气压、湿度数据变化,结合特征大气吸收衰减模型进行衰减修正,计算得到降雨过程中微波的衰减修正值AModi,因此仅由降雨因素造成的微波传输衰减Arain可由(4)式计算:

2.3 非球形雨衰模型

降雨粒子的形状取决于粒子的尺度,一般而言,降雨粒子的直径在10µm—10 mm之间,大于7 mm的降雨粒子是不稳定的,容易发生破裂.研究表明,等效半径小于1 mm的降雨粒子基本为球状粒子;等效半径达到1.5 mm时,降雨粒子的形状近似为一个扁旋转椭球体;当等效半径达到2 mm时,降雨粒子的形状变成一个底部扁平的扁旋转椭球体;当等效半径达到2.75 mm时,椭球体形状的降雨粒子底部形成一个凹槽,但是这种尺度的降雨粒子在我国很少出现.

2.3.1 PB降雨粒子模型

降雨粒子的形状通常用粒子的轴比来表示,轴比为椭球体短轴与长轴之比:

式中,a为椭球体短轴,b为长轴.

Pruppacher和Beard[17]在风洞实验实测数据的基础上进行分析,认为降雨粒子的轴比和粒子等效直径之间进行存在线性关系,提出了PB模型:

式中,Deq为降雨粒子等效直径.

2.3.2 基于 TT 矩阵理论计算降雨粒子消光截面

T矩阵理论(extended boundary condition method)是对任意形状粒子的Maxwell方程的严格解析解[23].假设电磁波入射到空间粒子上:

对入射场、散射场按矢量球面波展开如下:

式中,k1为周围介质的波数;RgMmn,RgNmn,Mmn和Nmn是矢量球谐函数.入射场的展开系数amn,bmn表示如下:

式中,C∗mn,B∗mn为球矢面变量.由于Maxwell方程及边界条件是线性的,散射场的展开系数pmn和qmn与入射展开系数amn和bmn之间也是线性的.利用假设的转换矩阵T给出如下关系:

对(12)和(13)式采用矩阵形式改写:

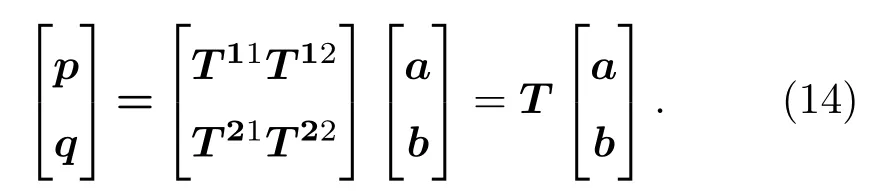
(14)式表明散射场的展开系数由T矩阵和入射场展开系数相乘获得,基于(14)式可计算得到粒子消光截面:

2.3.3 非球形雨衰模型

基于上述的T矩阵理论,计算得到PB降雨粒子模型的消光截面,根据雨致衰减理论公式计算理论雨致衰减[24],

式中,N(D)为Gamma雨滴谱分布(m−3·mm−1),其谱分布函数为

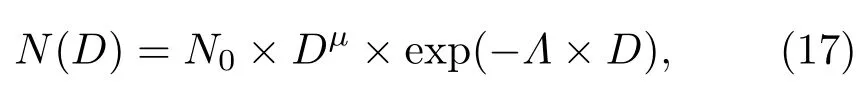
式中,N0为粒子数密度(m−3·mm−1+µ),Λ为尺度因子(mm−1),µ为形状因子,为无量纲量.

利用(16)式,根据OTT雨滴谱仪记录的Gamma谱参数历史数据和基于T矩阵理论计算的降雨粒子消光截面,计算得到微波理论雨致衰减,同时,OTT雨滴谱记录了相对应的降雨强度.对微波理论雨致衰减和实测雨强采用(1)式的雨衰幂律形式,利用LM最优化算法[25](Levenberg-Marquardt algorithm)进行非线性拟合,得到适用于实地气候雨滴谱特征的雨衰幂律模型.其拟合方法如下.

设定目标函数为

式中,Ri为实测降雨强度(mm/h),Ai为理论雨致衰减(dB/km).(18)式向量形式如下:

此时,拟合问题转化为求解最小化问题,

式中,x=[a,b],xopt=[aopt,bopt].

图2 (网刊彩色)微波雨衰模型拟合结果Fig.2.(color online)The f i tting results of rain-attenuation relationship.

求解的具体步骤如下:

步骤1 设定初始值x0,误差精度ε=10−5,计算目标函数Fopt(x0);

步骤2 令µM=0.001,k=0;

步骤3 求解δxk,计算Fopt(xk+1),δxk的计算公式为

式中,Jk为雅可比(Jacobi)矩阵在xk点的值,I为单位矩阵,xk+1的计算公式为xk+1=xk+δxk;

步骤4 如果µM=0,迭代结束,否则进行下一步;

步骤5 如果Fopt(xk+1)＞Fopt(xk),则令xk+1=xk+δxk,µM=10µM,并转入步骤3;否则,若δxk＜ε,则结束迭代,若δxk≥ε,令xk+1=xk+δxk,µM=0.1µM,转入步骤3.

图2为15—20 GHz基于非球形雨衰模型的拟合结果,其中OTT雨滴谱仪历史数据为2013年6月的南京地区Gamma雨滴谱和降雨强度的实测数据,对实测数据按分钟平均,得到4620个数据样本点.从图2可以看出,微波频率在15—20 GHz范围时,雨衰模型的幂律系数b接近1,说明在该频段范围,微波雨致衰减与降雨强度呈近似线性关系.

为定量评价拟合效果,采用拟合值与理论值间的均方根误差(root mean square error,RMSE)、标准化平均误差(normalized mean error,NME)和标准化平均偏差(normalized mean bias,NMB)对拟合结果进行评估.其中,RMSE反映的是拟合值与理论值之间的误差大小,NME和NMB反映的是拟合值与理论值之间的相对偏差,若NME和NMB的值均小于20%,表示拟合效果较好.从表1中可以看出,各频率下RMSE值均在0.04—0.05之间,NME值均在15%以下,NMB值在5.5%以下.评估结果表明,模型拟合值与理论值间相差较小,拟合误差较小,拟合精度较高.

图3分别给出了15—20 GHz频率范围内,微波在不同温度条件下非球形雨衰模型的幂律系数a,b值.由表可知,同一频率时雨衰模型参数a,b随温度的变化比较小,随着温度升高,a值逐渐变大.当微波频率为15 GHz时,b值随温度的变化不明显,在16—19 GHz时,b值随温度的升高呈下降趋势.同时可以发现,微波频率越高,a值呈上升趋势,b值呈下降趋势.

图4是在温度为25°C时,幂律关系中的b值随频率的变化情况.从图4可以看出,频率越高,b值越小.微波频率在32 GHz左右时,b值接近1,说明在此频率下微波雨致衰减与降雨强度接近呈线性关系.

表1 微波雨衰模型拟合结果Table 1.The f i tting results of rain-attenuation relationship.

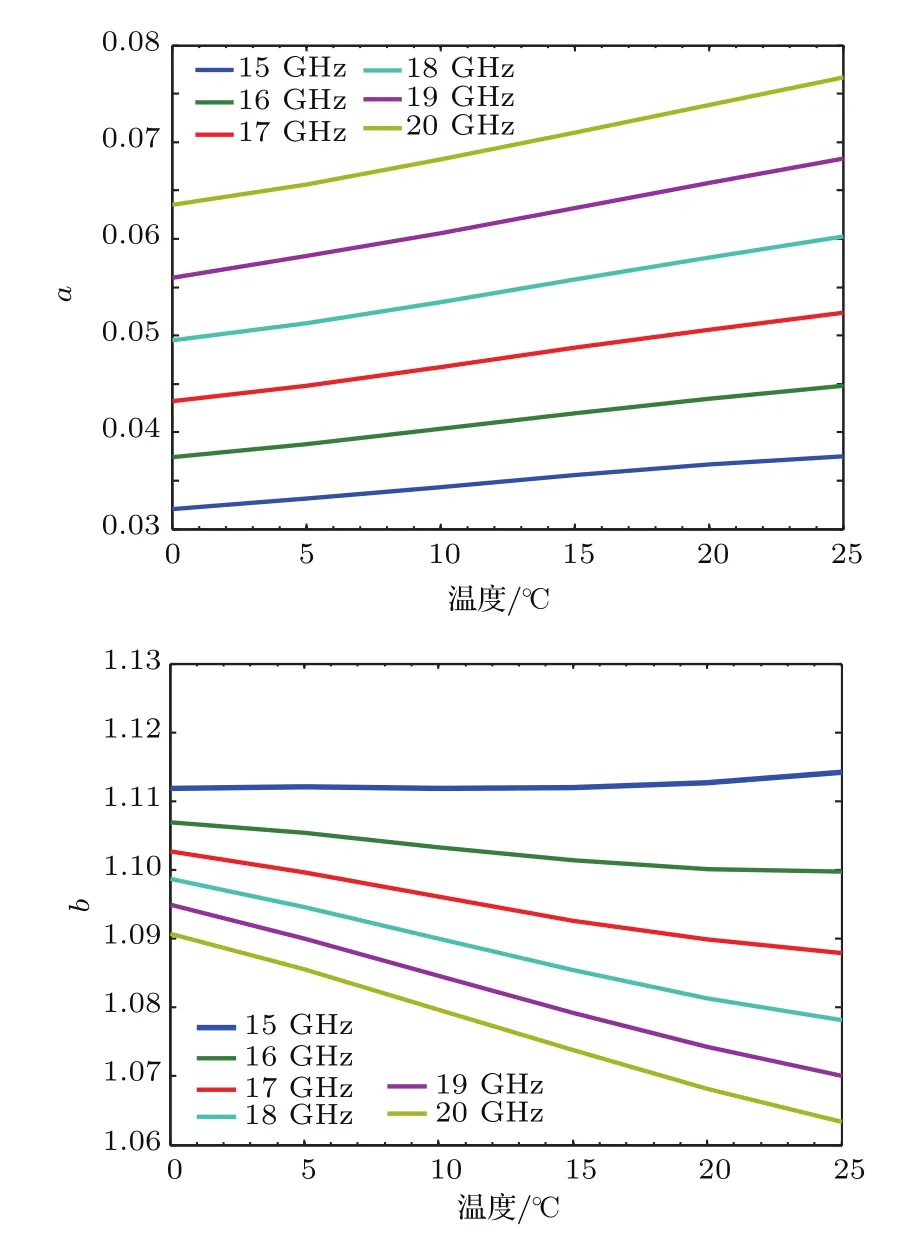
图3 (网刊彩色)非球形雨衰模型幂律系数Fig.3.(color online)Power-law relationship for different temperature and frequency.

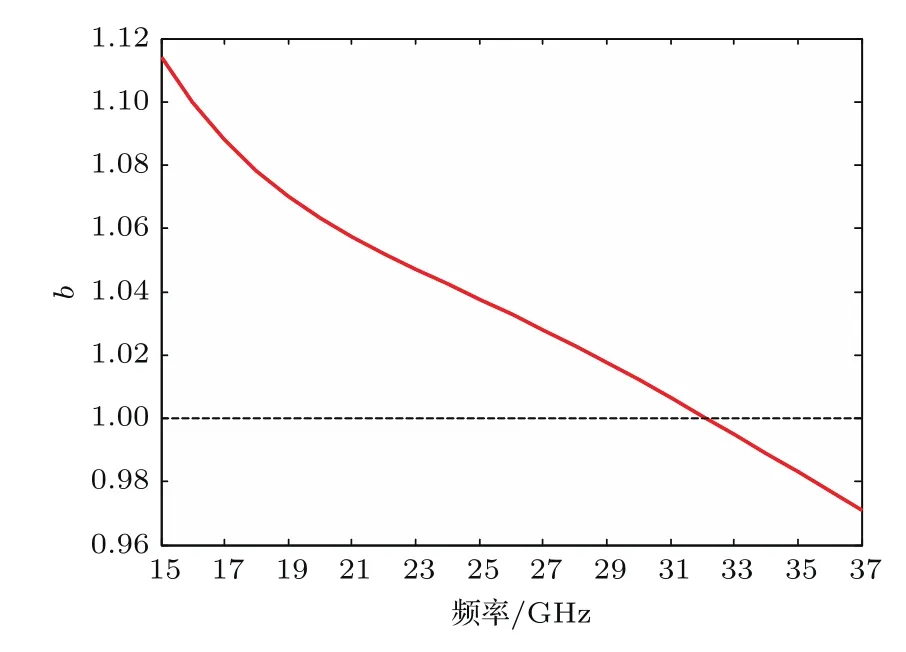
图4 (网刊彩色)非球形雨衰模型b值 (25°C)Fig.4.(color online)b in power-law relationship for different frequency(25 °C).

3 微波链路测量实验及结果分析

不同类型降雨的雨滴形状是类似的,其差别主要体现在雨滴谱分布上,因此非球形雨衰模型在理论上可适用于不同类型的降雨.为了检验非球形雨衰模型反演降雨强度的准确性,本文针对南京地区一次层状云降雨事件,开展了15—20 GHz频段的视距微波链路反演路径降雨实验,进行个例分析,并与OTTPARSIVEL激光粒子谱仪进行同步对比.本次实验时间段为2013年7月5日13:00—18:00及7月6日11:00—14:00,实验区域介于南京市江宁区和玄武区之间,整个实验覆盖了从暴雨、大雨、中雨、小雨到毛毛雨的全部过程.实验链路长度为6.57 km,微波发射机型号为Anritsu MG3694B信号发生器,信号接收机型号为Agilent E4440A频谱分析仪,微波发射和接收天线均采用定向天线,信号传输为屏蔽电缆,以保证微波信号免受外界干扰,实现微波信号的无损接收.微波发射机的发射功率为14 dBm,接收机的采样间隔为15 s,其分辨率为0.01 dB.

图5和图6分别给出了2013年7月5日和7月6日基于非球形雨衰模型反演结果与OTT雨滴谱仪测量值的对比.从实验结果可以看出,基于非球形雨衰模型反演的降雨强度与OTT雨滴谱仪观测的降雨强度之间均存在较好的相关性.对于降雨强度和累积降雨量,与OTT雨滴谱仪的实测雨强相比,非球形雨衰模型反演的雨强偏大.需要强调的是,降雨在空间分布是不均匀的,OTT雨滴谱仪只能测量单点降雨情况,而微波链路反演的是微波传输路径的平均雨强.因此微波链路反演的雨强值与OTT雨滴谱仪观测的降雨强度无法完全一致.

为进一步检验模型反演效果,本文定量分析了基于非球形雨衰模型的微波链路反演的降雨数据,采用雨强时序相关系数、均方根误差、累计降雨强度绝对偏差和累计降雨相对偏差进行评估,结果列于表2.

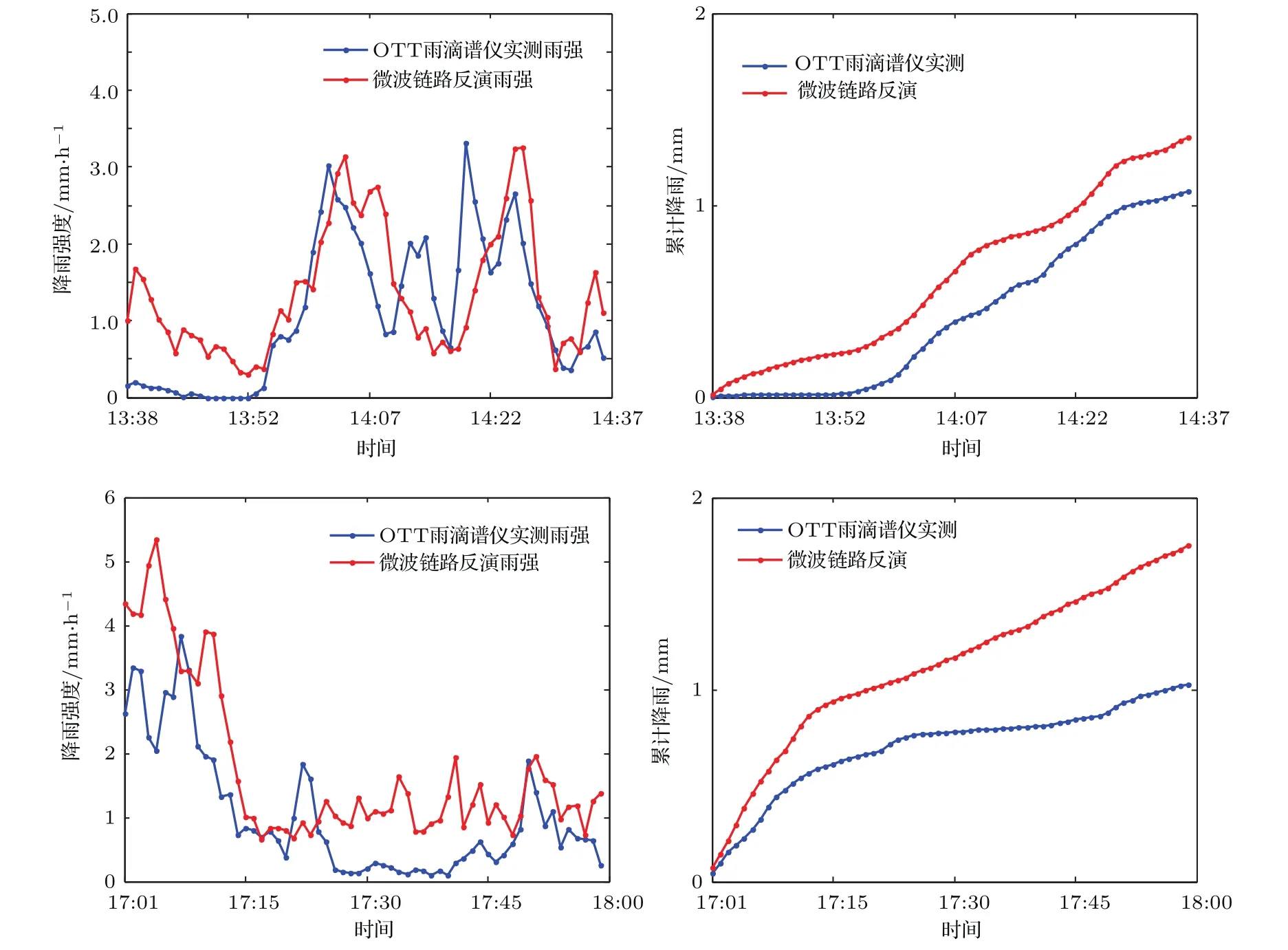
图5 (网刊彩色)微波链路反演降雨结果(2013年7月5日)Fig.5.(color online)Inversion results of microwave link(2013.07.05).

图6 (网刊彩色)微波链路反演降雨结果(2013年7月6日)Fig.6.(color online)Inversion results of microwave link(2013.07.06).

表2 微波链路降雨反演结果Table 2.Inversion results of microwave link.

由表2可知,基于非球形雨衰模型的微波链路降雨强度时序反演值与OTT雨滴谱仪实测的降雨强度值存在一定的相关性,相关系数都在0.6以上,最高达到了0.96,说明基于微波链路雨致衰减反演降雨强度具有一定的可行性;对于链路反演雨强的RMSE,其结果在0.79—3.67 mm/h之间.从累积降雨的绝对误差来看,结果在0.28—2.47 mm之间,说明微波链路反演的累积降雨量略高于OTT实测降雨强度;从相对偏差来看,反演结果在0.44%—1.84%之间,说明累积降雨量的反演结果较为理想.同时,从表2还可以看出,第一组实验的相关系数为0.65,低于其他三组,然而其对应雨强RMSE、累积降雨绝对偏差却低于其他三组试验的结果,原因主要为第一组实验降雨量较小,所以其反演值与实测值的绝对差值要小于其他三组,因而该组雨强RMSE、累积降雨绝对偏差小于另外三组,但从累积降雨相对偏差看,第一组实验大于其他三组,进而导致其相关系数较其他三组而言相对较低.

从表2还可以看出,非球形雨衰模型对小雨的反演精度低于中雨和大雨,其原因主要为降雨强度较小时,微波的雨致衰减值也较低,由于无法完全消除非雨致因素造成的微波衰减,因此降雨较弱时,非雨致微波衰减对反演精度的影响要大于强降雨时对反演精度的影响.

综上所述,本文提出的基于非球形雨衰模型的微波链路反演雨强方法的具有一定的可行性,基于T矩阵理论和PB降雨粒子模型,对OTT雨滴谱仪的Gamma谱参数历史资料与降雨强度值进行非线性拟合得到具有实地谱分布的幂律系数,建立适合于本地区的雨衰模型,便于进一步开展微波链路雨强反演研究.

4 结 论

本文以降雨粒子对电磁波的衰减效应为物理原理,以T矩阵理论、Gamma谱分布为理论基础,基于PB降雨粒子模型,提出了基于非球形雨衰模型的微波链路雨强反演方法,并对南京地区一次层状云降雨开展了15—20 GHz频段的视距微波链路反演路径降雨实验,对非球形雨衰模型进行验证.实验结果表明,反演雨强的相关系数全部高于0.6,最高达到了0.96,RMSE最小值为0.79,累积降雨量的绝对偏差在2.47 mm以内,最小偏差仅为0.28 mm,相对误差低于1.84%.本次实验结果验证了本文提出的基于非球形雨衰模型的微波链路雨强反演方法的准确性和可行性,对于进一步提高微波链路反演降雨精度、改善降水监测效果具有重要意义.

同时,实验结果也表明,非球形雨衰模型对小雨的反演精度低于中雨和大雨,主要是受非雨致因素造成的微波衰减的影响,降雨强度较小时,微波雨致衰减值较低,非雨致微波衰减对反演精度的影响要大于强降雨时对反演精度的影响,从而影响了雨强反演精度.因此,需要进一步开展消除非雨致微波衰减的工作.

[1]Gao T C 2012Meteorol.Hydrol.Eq.23 1(in Chinese)[高太长2012气象水文装备23 1]

[2]Lü D R,Wang P C,Qiu J H,Tao S Y 2003Chin.J.Atmos.Sci.27 552(in Chinese)[吕达仁,王普才,邱金恒,陶诗言2003大气科学27 552]

[3]Liang H H,Xu B X,Liu L P,Ge R S 2005Adv.Earth Sci.20 541(in Chinese)[梁海河,徐宝祥,刘黎平,葛润生2005地球科学进展20 541]

[4]Qie X S,Lü D R,Chen H B,Wang P C,Duan S,Zhang W X 2008Chin.J.Atmos.Sci.32 867(in Chinese)[郄秀书,吕达仁,陈洪滨,王普才,段树,章文星 2008大气科学32 867]

[5]Messer H,Zinevich A,Alpert P 2006Science312 713

[6]Feng G L,Gong Z Q,Zhi R,Zhang D Q 2008Chin.Phys.B17 2745

[7]Goldshtein O,Messer H,Zinevich A 2009IEEE Trans.Signal Proces.57 1616

[8]Messer H,Zinevich A,Alpert P 2012IEEE Trans.Instrum.Meas.15 32

[9]David N,Alpert P,Messer H 2013Atmos.Res.131 13

[10]Overeem A,Leijnse H,Uijlenhoet R 2013Proc.Natl.Acad.Sci.USA110 2741

[11]Liu X C,Liu L,Gao T C,Ren J P 2013J.Infrared Millim.Waves32 379(in Chinese)[刘西川,刘磊,高太长,任景鹏2013红外与毫米波学报32 379]

[12]Liu X C,Gao T C,Liu L,Zhai D L 2014Acta Phys.Sin.63 199201(in Chinese)[刘西川,高太长,刘磊,翟东力2014物理学报63 199201]

[13]Jiang S T,Gao T C,Liu X C,Liu L,Liu Z T 2013Acta Phys.Sin.62 154303(in Chinese)[姜世泰,高太长,刘西川,刘磊,刘志田2013物理学报62 154303]

[14]Yin M,Jiang S T,Gao T C,Liu X C,Liang M Y,Ge S R,Cao C K 2015Meteorol.Sci.Technol.43 1(in Chinese)[印敏,姜世泰,高太长,刘西川,梁妙元,戈书睿,曹承堃2015气象科技43 1]

[15]Gao T C,Song K,Liu X C,Yin M,Liu L,Jiang S T 2015Acta Phys.Sin.64 174301(in Chinese)[高太长,宋堃,刘西川,印敏,刘磊,姜世泰2015物理学报64 174301]

[16]International Telecommunication Union 2005Rec.ITURP.838-3

[17]Pruppacher H R,Beard K V 1970J.Quart.J.R.Met.Soc.96 247

[18]Michael I M,Larry D T 1998J.Quant.Spectrosc.Radiat.Transfer60 309

[19]Chen B J,Li Z H,Liu J C,Gong F J 1998Acta Meteorol.Sin.56 123(in Chinese)[陈宝君,李子华,刘吉成,宫福久1998气象学报56 123]

[20]Yuan C,Fan L,Li Y B 2001J.Nanjing I.Meteorol.24 250(in Chinese)[袁成,樊玲,李亚滨 2001南京气象学院学报24 250]

[21]Zheng J H,Chen B J 2007J.Meteorol.Sci.27 17(in Chinese)[郑娇恒,陈宝君 2007气象科学 27 17]

[22]FreemanR1991TelecommunicationsTransmission Handbook(3rd Ed.)(Canda:John Wiley&Sons Inc.)p279

[23]Somerville W R C,Auguie B,Ru E C L 2013J.Quant.Spectrosc.Radiat.Transfer123 153

[24]David C H,Chu T S 1975Proc.IEEE63 1308

[25]Lampton M 1997Comput.Phys.11 110