基于谱域相位分辨光学相干层析的纳米级表面形貌成像∗

王毅 郭哲 朱立达 周红仙 马振鹤

1)(东北大学秦皇岛分校控制工程学院,秦皇岛 066004)

2)(燕山大学电气工程学院,秦皇岛 066004)

1 引 言

材料微观表面形貌很大程度地影响着材料的性能和功能[1],微观表面形貌检测在工业产品检测、机械制造、电子工业等领域均有非常重要的应用价值.随着现代电子工业、光学精微加工及微机电技术的发展,对微观表面精度的要求越来越高,表面形貌质量成为保证和提高机械、电子及光学系统性能、质量和寿命的关键因素之一[2−5].在最近几十年里,国内外微观表面形貌测量领域出现了许多新技术和新方法,使测量精度不断提高,己从微米尺度进入到纳米甚至亚纳米尺度[6−9].

目前微观表面形貌测量方法可分为两大类:接触式和非接触式.触针式轮廓仪是目前使用比较广泛的接触式表面轮廓测量仪,具有测量范围大、分辨率高、测量结果稳定可靠、重复性好等优点,其轴向测量分辨率可达1 nm或更小[10],但是在微观表面轮廓检测中,通常要求不能和样品表面接触,接触检测会导致样品表面损伤.纳米级精度的非接触测量方法可分为非光学方法和光学方法两大类,非光学测量方法包括扫描隧道显微镜和原子力显微镜.扫描隧道显微镜横向分辩率为0.1 nm,轴向分辨率0.01 nm量级,其轴向和横向测量范围较小(约1µm).扫描隧道显微镜是通过隧道电流反映被测表面形貌,因此,只能测量导体或半导体,而且测量必须在真空中进行[11,12].原子力显微镜的轴向分辨率达到0.1 nm,横向分辨率约为10 nm,既可以检测导体,也可以检测非导体,但具有成像范围小、受探头影响大的缺点[13,14].纳米级光学测量方法分为两类:1)结合色差和共焦显微技术的色差共焦光谱(chromatic confocal spectrum,CCS)技术[15,16];2)干涉测量方法.干涉法包括:单色光相移干涉法(phase-shifting interferometry,PSI)、垂直扫描白光干涉法(vertical scanning white-light interferometry,SWLI)、白光光谱干涉法(white-light spectral interferometry,WLSI)及外差干涉法(heterodyne interferometry,HI)[17−21].

轴向分辨率、轴向测量范围、系统稳定性、横向分辨率及检测速度是纳米级形貌成像中比较关键的问题.CCS轴向分辨率达到2 nm,差于干涉法,但是CCS技术的优点是稳定性高.CCS技术的另一缺点是其轴向分辨率、轴向测量范围及横向分辨率都决定于样品的光焦点,轴向分辨率、轴向测量范围是依赖于焦点色散特性,因此,要求焦点色散特性严格稳定,不适合于进行快速的光学扫描,目前都是用高精度平移台移动样品进行二维扫描.平移台移动会引入振动干扰,影响轴向测量精度,同时也限制了测量速度.干涉方法影响系统性能的主要因素是稳定性和轴向测量范围,该方法灵敏度高,但对外界的干扰也同样灵敏.干涉法的轴向精度和横向分辨率无关,可以实现快速的光学扫描.

干涉法的轴向分辨率要高于CCS技术,但是存在相位包裹及易受环境干扰的问题.PSI,WLSI及HI是通过计算参考光和样品光之间的相位差得到样品表面的高度值,相位计算的主值范围为[−π,+π],当相位超过[−π,+π],会发生相位包裹,必须通过相位解包裹恢复真实相位,才能得到正确的高度信息[6].目前,虽然已提出了多种数值相位解包裹的方法,然而这些方法都存在一定的问题,如计算复杂耗时、受噪声及欠采样影响,特别是当相邻两点相位差超过π时,无法恢复真实的相位[22,23].相位解包裹的原理是根据相位的连续性,通过比较相邻两点之间的相位差进行相位解包裹.从原理上讲,当相邻两点的相位差大于π时,就无法正确恢复真实相位,这就限定了干涉法的应用范围.SWLI可以测量绝对光程,不存在相位包裹问题,但是对于每一个探测点都需要进行轴向扫描,干涉条纹的解调精度和轴向扫描精度限制了轴向测量精度,同时使用轴向扫描也限制了测量速度.

光学相干层析(optical coherence tomography,OCT)是一种具有高时间分辨率和高空间分辨率的非接触、三维成像技术,其轴向分辨率取决于光源的相干长度,一般可以达到1—10µm.目前,OCT在眼科临床诊疗及血流成像中获得了广泛的应用[24,25],也被用于表面形貌成像[26−28],但是其轴向分辨率仅为微米量级.文献[29,30]使用时域OCT分别实现了0.64µm和0.75µm的轴向分辨率,文献[31]利用超连续谱光源实现了谱域OCT 0.9µm的轴向分辨率.本文在谱域相位分辨OCT的基础上,建立了一种纳米级表面形貌成像系统,由干涉光谱经过傅里叶变换得到包含各点相位信息的复数,计算相邻两位置的相位差,得到表面形貌的相位差分图,经过积分,得到样品表面形貌的定量分布.由于不直接计算各个位置的相位,因此,只要相邻两点的相位差在区间[−π,+π],就不会发生相位包裹,将干涉法相邻两点相位差绝对值的限制条件由目前的π扩大到2π.为了提高系统的稳定性,参考面和样品置于同一平台之上,最大限度地消除环境干扰及系统振动的影响.使用光学扫描实现高速成像,减小了使用二维平移台引入的干扰,实验表明本系统轴向分辨率优于1 nm.

2 装置及方法

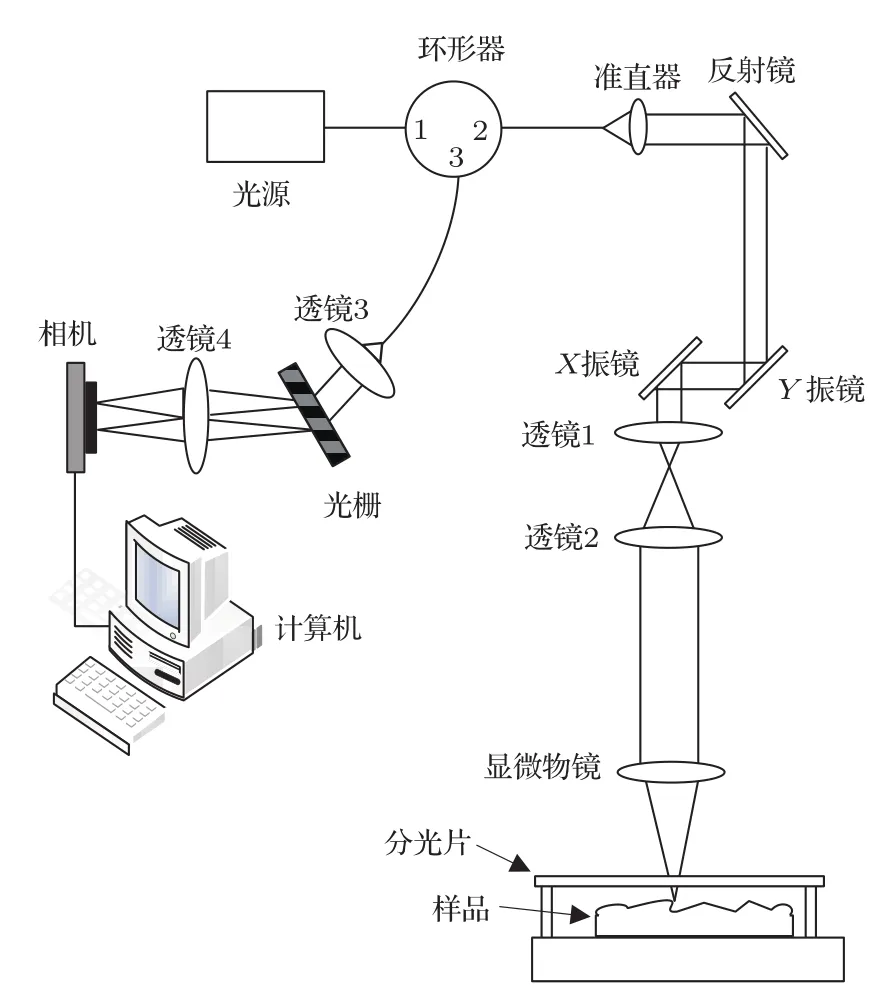
图1 实验装置原理图Fig.1.Schematic of the experimental setup.

实验系统如图1所示,为参考光和样品光共光路的OCT系统.光源为超辐射发光二极管(superluminescent diode,SLD),中心波长为1310 nm,带宽为62 nm.SLD发出的光经过光纤环形器后,由准直器准直成平行光,经X-Y振镜进行二维扫描,光路和激光扫描共焦显微镜的光路类似,准直光照射到X振镜的光斑位于透镜1的焦点,透镜1和透镜2的间距为透镜1和透镜2焦距之和,透镜2和显微物镜的间距为两者的焦距之和.这样,可以保证照射在样品上的光接近垂直.透镜1和2的作用是扩束,然后经过长工作距离显微物镜聚焦到样品表面,用一个分光片的下表面作为参考面,样品表面反射的光为物光,分光片下表面反射的光为参考光,样品上表面和分光片下表面形成高度大约为100µm的间隔,物光和参考光沿原路返回到环形器,由环形器的出口3进入自建的高速光谱仪.光谱仪主要包括一个透射光栅(1145 lines/mm,Wasatch Photonics)和高速线阵相机(GL2048L,Sensors Unlimited),使用12位图像采集卡(PCI1433,NI),由光谱仪实时采集干涉光谱,将干涉光谱传给计算机进行处理.

为了减小波数非线性及色散的影响,我们使用多项式进行光谱仪校准,再通过插值,得到以线性波数值表示的干涉光谱[32].下面以相邻位置1和2两点为例,说明相位计算方法.假定位置点1的相干光谱为[33]

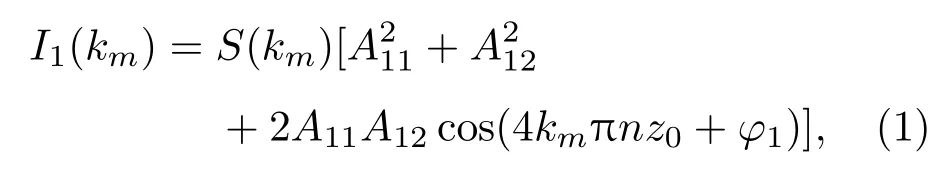
其中,km为离散化的波数,S(km)为光源光谱强度分布,A11和A12分别为位置1对应的样品光和参考光振幅,n为空气折射率.在相位分辨OCT中,样品面和参考面的距离用不同分辨率的两部分表示,(1)式中z0表示样品面和参考面的绝对距离,其精度决定于光源的相干长度,相对于z0的具有亚相干长度分辨率的距离为δz=φ1/(4kcπn),kc为光源的中心波数,其精度决定于光谱仪的光谱分辨率.假定位置点2的相干光谱为I2(km),假定位置点2相对于点1的微小高度增量为Δz0,则有

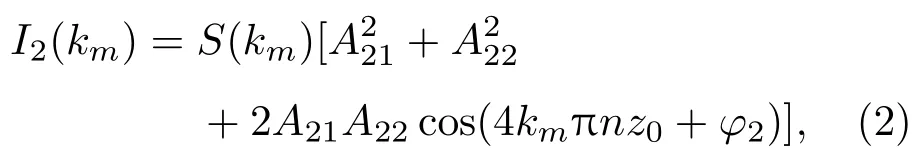
其中,A21和A22分别为位置2对应的样品光和参考光振幅.假定位置点1和2的参考臂光程相等,则位置点1和2的高度差Δz0为

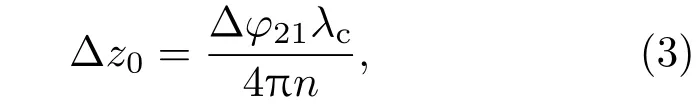
其中,Δφ21为φ2与φ1之差. 对I1(km)和I2(km)分别进行傅里叶变换后得到相对应的复数序列F1(2nzm)和F2(2nzm),zm表示离散化的高度.因为样品中只有样品表面为反射面,则F1(2nzm)和F2(2nzm)的功率谱极大值对应的位置即为2nz0,因此得到两个复数F1(2nz0)=A1exp(j4kcπnφ1)和F2(2nz0)=A2exp(j4kcπnφ2),则Δφ21为

式中星号表示复共轭.由(4)式计算出相位差Δφ21,即得到样品表面的相位差分图,不论各点的相位值大小,只要相邻两点在区间[−π,+π],就不会发生相位包裹;当相邻两点的相位差超过π,在相位差分图上出现相位包裹,通过相位解包裹处理,消除相位差分图上的相位包裹,再进行积分,得到样品表面的相位分布及形貌.由于解包裹运算是在相位差分图上进行的,因此,把相邻两点相位差绝对值的限制条件由目前的π扩大到2π.

3 实验结果与讨论

3.1 系统性能验证

对于纳米级精度的测量,系统的稳定性对测量结果影响很大.首先进行实验确定系统的稳定性,用该系统连续检测同一点,由该点高度随时间的涨落,确定系统的稳定性.测量结果如图2所示,这些结果是系统噪声和外界干扰总的影响结果.为了直观地显示涨落程度,将信号的基线平移到零点,用常用的粗糙度参数Ra和Rt表示系统的噪声当量[21],Ra表示偏差绝对值的算术平均,Rt表示最大值和最小值之差.图2(a)为直接测量的高度涨落,图2(b)和图2(c)分别为5次平均和10次平均的结果.图2(a)—(c)显示,本系统在单次、5次平均及10次平均的情况下,Rt和Ra分别为:单次(Rt=0.48 nm,Ra=0.06 nm),5次平均(Rt=0.24 nm,Ra=0.03 nm),10次平均(Rt=0.17 nm,Ra=0.02 nm),信噪比为103 dB.作为对照,本系统使用独立的参考臂和探测臂时的单次测量结果如图2(d)所示,其Rt和Ra分别为48.62 nm和5.74 nm,说明环境干扰对干涉测量的影响较大.共光路模式下的噪声约为非共光路模式下噪声的百分之一,抗干扰能力和灵敏度达到纳米级检测的要求.图2(e)和图2(f)分别为图2(a)和图2(d)所示结果的直方图,两者的标准差分别为0.076 nm和7.2 nm,和非共光路模式相比,共光路模式的精确度提高了两个数量级.

图2 系统稳定性实验结果 (a)共光路模式的测量结果;(b)为(a)的5点平均结果;(c)为(a)的10点平均结果;(d)非共光路模式的测量结果;(e)为(a)的直方图;(f)为(d)的直方图Fig.2.Experimental results for testing the systemic stability:(a)Results measured with common-path;results obtained by averaging f i ve points and ten points of(a)are shown in(b)and(c),respectively;(d)results measured using separated reference and probe arms;(e)histogram of the data in(a);(f)histogram of the data in(d).

我们通过测量纳米级压电位移台的位移,评估系统的准确度,选用PI公司P-260纳米级精密压电位移台,P-620位移台的标称重复性为±1 nm,在实验室环境下,该系统自检的重复性为±2 nm.图3(a)为压电位移台阶跃位移的测量结果,阶跃高度自上而下分别为10,15,20,25,30 nm,测量结果的涨落为±2 nm,和该平移台±2 nm的重复性符合,说明测量结果±2 nm的涨落主要来源于该压电位移台.图3(b)为阶跃高度的计算结果(平台上下面各取50点平均),横坐标表示压电位移台的阶跃高度设定值,为5—30 nm,55—80 nm,110—130 nm,步长都为5 nm,黑色圆圈表示设定值,蓝色星表示测量值,红色直线和红色方框表示测量结果的线性拟合,拟合相关系数R2为0.9996,表明两者有非常好的符合度,测量结果有很好的线性.可以看出,设定值和方框代表的拟合值完全符合,测量值和设定值的最大偏差为2.08 nm,各次测量的平均绝对偏差为0.62 nm.

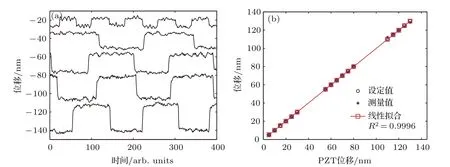
图3 (网刊彩色)系统准确性实验结果 (a)对纳米级压电位移台阶跃位移的测量结果;(b)阶跃高度的计算结果,黑色圆圈表示设定值,蓝色星表示测量值,红色直线和红色方框表示测量结果的线性拟合Fig.3.(color online)Experimental results for testing the systemic accuracy:(a)Measured results of step displacements of a nanoscale Piezo stage;(b)measured step heights,where the black circles,the blue stars and the red line denote the preset value,the measured results and the f i tted results,respectively.

3.2 压电位移台振动检测

目前的干涉检测都是直接计算各点的绝对相位,当某一点的相位超过[−π,+π],则产生相位包裹.我们计算相邻两点的相位差,相邻两点的相位差的绝对值超过π才出现相位包裹.通过测量压电位移台的振动说明本方法的特点,选用PI公司的P-620型压电位移台,将图1中的分光片固定,用压电位移台驱动反射镜运动,反射镜的反射面和分光片之间的间隙大概为100µm,连续检测反射镜一点的振动,计算相邻两个时间点所采集信号的高度差,再经过积分得到探测点高度随时间的变化,结果如图4所示.图4(a)为幅度为20nm、频率为3Hz的三角波的检测结果,图4(b)和图4(c)是幅度为800 nm、频率为3 Hz的正弦波结果,图4(b)为使用本文方法计算的结果,图4(c)为使用目前直接计算相位的方法的结果.图4(a)和图4(b)显示本系统与实际符合得很好,说明该系统检测的结果是可信的;在图4(a)中有较明显的偏离,这是因为该压电位移台的精度为±2 nm所导致.图4(c)显示的结果出现相位包裹,两条短划横线表示的位置为±327.5 nm,对应的相位为±π.我们计算相邻两点的相位差,除非变化较大的边界,通常情况下不会产生相位包裹,如图4(b)所示.

3.3 分辨率片表面形貌成像

对USAF1951分辨率片的表面形貌进行成像,验证本系统的性能,分辨率片是通过蒸镀铬在玻璃上形成不同宽度的条纹,对分辨率正片上的镀铬层进行成像,结果如图5所示.由于本系统的轴向精度和横向分辨率无关,并且使用光学扫描,所以,可以通过改变扫描振镜的驱动电压及显微物镜的放大倍数,对不同大小范围成像.图5(a)—(c)使用4倍显微物镜,成像范围为1.1 mm×1.1 mm,显示了分辨率片4—7组的全部线对.在图5(a)中,图像灰度值代表高度,黑色表示玻璃基板,白色为镀铬层,其三维显示如图5(b)所示,可以清晰地看到镀铬层的结果.图5(c)是直接计算各点相位的结果,出现了明显的相位包裹.对图5(a)中红色矩形框所示区域进行成像,结果如图5(d)所示,成像范围为432µm×432µm,在镀铬层结构的边缘出现钝化,这是因为使用了低数值孔径的显微物镜(4倍,NA=0.1).使用高数值孔径的显微物镜(20倍,NA=0.42)对图5(a)中黄色矩形框所示区域成像的结果如5(e)所示,成像范围为138µm×138µm,可以清晰地显示镀铬的细微结构和蒸镀错误的结构,如图中箭头所示.

3.4 表面粗糙度标准样板的表面形貌成像

在机械加工过程中,由于刀具和零件的摩擦、切削分离时的塑性变形和金属撕裂,以及加工系统中的高频振动等原因在零件的加工表面上残留各种不同形状和尺寸的微观凸峰和凹谷,常常需精确可靠地测量零件的表面形貌.用本系统对表面粗糙度标准样板进行成像,表面粗糙度标准样板是以比较法来检查机械零件加工表面粗糙度的一种工作量具,对其中的0.1级平磨标准样板(Ra=0.1µm)表面形貌进行成像,结果如图6所示,可以清晰地看到平磨产生的沟槽,以及砂轮颗粒和材料表面作用产生的微观齿状磨痕,如图中箭头所示,可以直观地显示加工质量.

3.5 讨 论

目前的PSI,WLSI及HI等是直接计算各点的相位差,由于一般情况下参考光和样品光的光程差远大于波长,当相位差超过[−π,+π],则产生相位包裹,如图4(c)和图5(c)所示,虽然通过相位解包裹处理,可以恢复连续的相位分布,但是系统噪声及欠采样会导致相位解包裹错误,从原理上讲,当相邻两点的相位差超过π,将无法恢复真实的相位,这就限定了干涉法的应用范围.本系统使用相位分辨OCT的相位计算方法,首先由傅里叶变换得到和高度相关的复数序列,由(4)式计算相邻两点的相位差,然后通过积分,得到高度分布.因此,只有当两点之间相位差绝对值超过π才出现相位包裹,故在图4(b),图5(a)、(b)、(d)和(e)以及图6的计算中,并不会出现相位包裹,这样就避免了相位解包裹过程中可能的错误.对于变化较大的边界,当相邻两点相位差绝对值超过π,在相位差分图上出现相位包裹,首先使用目前的相位解包裹算法对相位差分图进行恢复,再进行积分,得到样品表面的相位分布,当相位差分图上两点之间的相位差绝对值超过π,同样无法正确恢复真实相位.由于解包裹是在相位差分图上进行的,因此,把相邻两点相位差绝对值的限制条件由目前的π扩大到2π,提高了干涉法的适用范围.

图2的系统稳定性实验表明,本系统单次测量的标准差为0.076 nm,表明本系统有非常高的重复性及抗干扰能力,对于纳米级精度检测,干扰是十分重要的问题,图2(d)表明使用独立的参考臂和样品臂,外界的干扰非常严重.在本系统中,样品光和参考光共光路,可以消除环境对样品光和参考光的影响,同时,由于参考面和样品置于同一平台之上,参考面随样品一起振动,可以最大限度地消除系统振动的影响.图3所示的测量结果表明本系统有较高的准确度,图3(a)中测量结果的涨落范围为±2 nm,这和该压电位移台系统的重复性符合.为了减小由于波数非线性及色散等原因引入的非线性影响,我们在进行干涉光谱的傅里叶变换之前,对干涉光谱进行了波数空间的线性矫正及色散矫正.另外,对于纳米级的测量,其量程一般限定在一个比较小的范围内,因此这种非线性的影响较小,图3(b)所示测量结果显示出了较好的线性.图3(a)中,各次测量的平均绝对偏差为0.62 nm,测量值和设定值的最大偏差为2.08 nm,这可能来源于外界的干扰,因为在进行PZI的位移测量时,固定于压电位移台的探测面独立于参考面运动,无法完全消除系统的振动.

图5 (网刊彩色)分辨率片表面形貌成像 (a)表面轮廓高度图,使用4倍显微物镜,扫描步长为3.3µm;(b)为(a)的三维显示结果;(c)使用目前的相位计算方法计算(a)的结果;(d)为(a)中红色框内表面轮廓成像结果,使用4倍显微物镜,扫描步长为1.44µm;(e)为(a)中黄色框内表面轮廓成像结果,使用20倍显微物镜,扫描步长为0.46µmFig.5.(color online)Surface topography of an optical resolution test target:(a)Topographic height map using a 4× objective and a scanning step of 3.3µm;(b)three dimensional-rendering image of(a);(c)wrapped image of(a)calculated by the traditional method;(d)topographic map of the area in the red box shown in(a),measured with a 4× objective and a scanning step of 1.44 µm;(e)topographic map of the area in the yellow box shown in(a),measured with a 20× objective and a scanning step of 0.46 µm.

本系统的成像速度主要决定于线阵相机速度,对于300×300点阵的图像,信号采集时间为5 s,线采样速度为18 kHz,成像速度远高于使用二维平移台的系统.在不影响轴向分辨率的情况下,可以改变扫描振镜的电压及使用不同放大倍数的物镜,形成不同的成像范围.本系统的横向分辨率由物镜数值孔径决定,使用不同的显微物镜对应不同的横向分辨率,当使用20倍显微物镜(NA=0.42)时,对分辨率板的成像结果显示可以清晰地分辨7组6级的线对,因此本系统使用20倍物镜时,分辨率优于2.19µm,使用更高数值孔径的物镜,横向分辨率可以进一步提高.

在(3)式中,假定相邻两点的参考光程相等,在实际应用中,作为参考的分光片相对于入射光会产生一定的倾斜,则相邻两点的参考光程存在一个固定的差值,重建的表面形貌会产生同样角度的倾斜,可以根据表面形貌中基线的倾斜程度通过高度补偿消除.

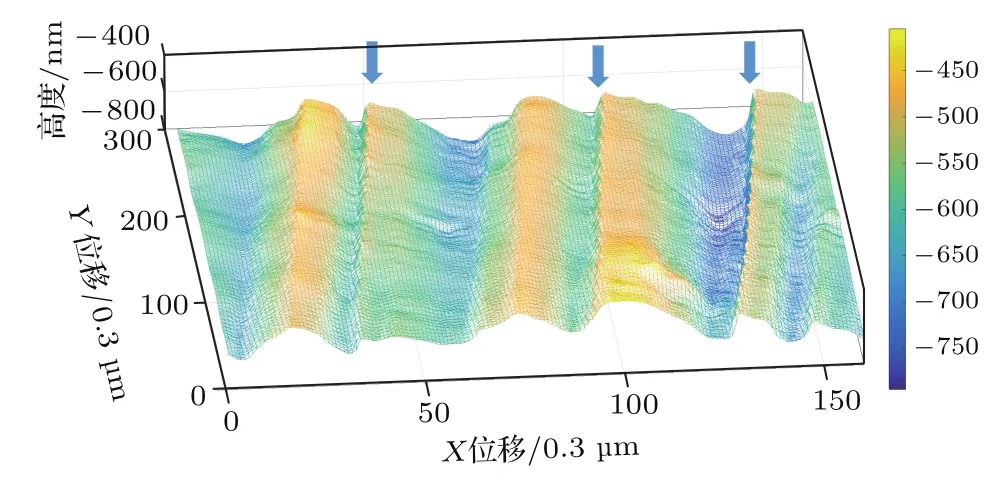
图6 (网刊彩色)表面粗糙度标准样板表面形貌成像Fig.6.(color online)Surface topography of a roughness comparison specimen.

4 结 论

传统OCT的轴向分辨率仅为微米量级,本文使用谱域相位分辨OCT实现了纳米级表面形貌成像,由于不用直接计算各个位置的相位值,只要相邻两点相位差绝对值小于π(目前干涉法的适用范围),则不发生相位包裹,避免了解包裹的可能错误.当相邻两点相位差绝对值超过π,在相位差分图上出现相位包裹,通过相位解包裹进行恢复,把相邻两点相位差绝对值的限制条件由目前的π扩大到2π,提高了干涉法的适用范围.为了消除外界干扰,使用共光路模式,消除了环境对参考光和样品光的影响,同时参考面和探测面置于同一平台之上,两者一起振动,最大限度地消除了环境干扰及系统振动的影响,使用光学扫描实现高速成像,并减小了使用二维平移台引入的干扰.实验结果表明本文提出的方法可以用于纳米级表面形貌快速成像,为纳米级表面形貌成像提供了一种新的工具.

[1]Thomas T R 2013Sur.Topogr.Metrol.Prop.2 014001

[2]Heintze S D,Forjanic M,Rousson V 2006Dent.Mater.22 146

[3]Song R L,Liu P,Zhang K,Liu X K,Chen X H 2016Chin.J.Mater.Res.30 255(in Chinese)[宋瑞利,刘平,张柯,刘新宽,陈小红2016材料研究学报30 255]

[4]Leyva-Mendivil M F,Lengiewicz J,Page A,BressloffN W,Limbert G 2017Tribol.Lett.65 12

[5]Wang J D,Chen D R,Kong X M 2003Tribology23 52(in Chinese)[汪家道,陈大融,孔宪梅2003摩擦学学报23 52]

[6]Groot P D 2015Adv.Opt.Photon.7 1

[7]Bruzzone A A G,Costa H L,Lonardo P M,Lucca D A 2008CIRP Annals-Manufact.Technol.57 750

[8]Leach R K,Giusca C L,Naoi K 2009Measur.Sci.Technol.20 125102

[9]Wang D,He C,Stoykovich M P,Schwartz D K 2015ACS Nano9 1656

[10]Guenther K H,Wierer P G,Bennett J M 1984Appl.Opt.23 3820

[11]Labella V P,Ding Z,Bullock D W,Emery C,Thibado P M 2000J.Vacuum Sci.Technol.A18 1492

[12]Schouteden K,Lauwaet K,Janssens E,Barcaro G,Fortunelli A,van Haesendonck C 2014Nanoscale6 2170

[13]Ando T,Uchihashi T,Scheuring S 2014Chem.Rev.114 3120

[14]Butt H J,Cappella B,Kappl M 2005Surf.Sci.Rep.59 1

[15]Duque D,Garzón J 2013Opt.Laser Technol.50 182

[16]Shi K,Li P,Yin S,Liu Z 2004Opt.Express12 2096

[17]Cai H,Guangyao L I,Huang Z 2016Laser Technol.40 20(in Chinese)[蔡怀宇,李光耀,黄战华 2016激光技术40 20]

[18]Lehmann P,Kühnhold P,Xie W 2014Measur.Sci.Technol.25 065203

[19]Liu C,Chen L,Wang J,Han Z G,Shi L L 2011Optoelectronic Eng.38 71

[20]Lin H,Li Y,Wang D,Tong X,Liu M 2009Appl.Opt.48 1502

[21]Zhou Z F,Zhang T,Zhou W D,Li W J 2001Optoelectronic Eng.28 7(in Chinese)[周肇飞,张涛,周卫东,李文杰2001光电工程28 7]

[22]Liu S,Yang L X 2007Opt.Eng.46 051012

[23]Goldstein G,Creath K 2015Appl.Opt.54 5175

[24]Huang D,Swanson E A,Lin C P,Schuman J S,Stinson W G,Chang W 1991Science254 1178

[25]Wang R K,An L 2009Opt.Express17 8926

[26]Ortiz S,Siedlecki D,Remon L,Marcos S 2009Appl.Opt.48 6708

[27]Ortiz S,Siedlecki D,Pérezmerino P,Chia N,Castro A D,Szkulmowski M 2011Biomed.Opt.Express2 3232

[28]Sun M,Birkenfeld J,Castro A D,Ortiz S,Marcos S 2014Biomed.Opt.Express5 3547

[29]Xue P,Fujimoto J G 2008Sci.Bull.53 1963

[30]Povazay B,Bizheva K,Unterhuber A,Hermann B,Sattmann H,Fercher A F,Drexler W,Apolonski A,Wadsworth W J,Knight J C,Russell P S,Vetterlein M,Scherzer E 2002Opt.Lett.27 1800

[31]Tang T,Zhao C,Chen Z Y,Li P,Ding Z H 2015Acta Phys.Sin.64 174201(in Chinese)[唐弢,赵晨,陈志彦,李鹏,丁志华2015物理学报64 174201]

[32]Ma Z,He Z,Wang S,Wang Y,Li M,Wang Q,Wang F 2012Opt.Eng.51 063203

[33]Tomlins P H,Wang R K 2005J.Phys.D:Appl.Phys.38 2519