三维弹性波逆时偏移中多卡GPU的应用

沈骥千

（江苏煤炭地质物测队，南京 210046）

三维弹性波逆时偏移中多卡GPU的应用

沈骥千

（江苏煤炭地质物测队，南京 210046）

地震勘探对象的日益复杂化，对成像效果提出了更高的要求。逆时偏移在理论上可以对复杂构造准确成像，且二维逆时偏移的研究也取得了一系列成果。而逆时偏移巨大的存储、计算量以及野外单炮数据量的庞大，已成为制约其在三维多分量资料中应用的瓶颈。针对有效边界存储在三维逆时偏移中存储较大的问题，采用随机边界条件以降低逆时偏移存储量并提高偏移效率。该边界条件无需保存各分量在边界处的波场值，即可实现正向延拓波场的逆时重构；考虑到三维逆时偏移需开辟较大数组空间用于计算，提出应用区域分解技术将计算数据分配到不同节点，实现基于MPI+CUDA的协同并行。SEG/EAGE盐丘模型算例证明了上述方法的有效性。

三维弹性波逆时偏移；随机边界；区域分解；MPI+CUDA协同并行

0 引言

基于标量波理论的反射纵波勘探技术在以往的能源开发过程中发挥了重要作用，但随着油气开发对地震勘探精度要求的不断提高和勘探目标构造和岩性复杂程度的不断增加，纵波勘探精度的提高越来越受制于其理论上的局限与波场信息单一等缺陷，在碳酸盐岩裂缝性储层、煤层气和页岩气储层等的勘探方面难以获得满意效果。近年来，以矢量波动理论为基础的多波地震勘探技术引起了业界的广泛重视，同常规纵波勘探技术相比，多波地震技术的理论假设与实际情况更为接近，且横波在复杂介质中具有独特的传播机理，故理论上多波地震技术解决实际问题的能力更强，更有利于提高勘探精度或实现某些特殊目标的精确勘探。

叠前深度偏移是多波地震技术的重要研究内容，对多波地震资料进行叠前深度偏移处理的意义在于：一方面，地下构造的精确成像需要借助高精度的叠前偏移技术来实现；另一方面，多波偏移剖面中所包含的地震波动力学特征还可用于岩性和流体识别；同时偏移得到的共成像点道集还可为振幅随偏移距变化（AVO）、振幅随入射角变化（AVA）或其它叠前反演工作提供输入数据。因此，多波地震资料偏移应当实现两个目标：（1）地下构造的纵、横波准确成像；（2）获取保真的纵横波叠前反演道集和叠加剖面。

基于弹性波理论的多分量地震资料联合逆时偏移技术是实现多波地震纵横波偏移成像的有效工具[1]。一方面，弹性波逆时偏移技术以双程波动方程为理论出发点，它无倾角限制，理论上可实现任意复杂构造的成像[2-5]；另一方面，相较于标量波动方程逆时偏移，多分量联合逆时偏移保留了地震波的弹性、矢量特征，可以对气云带等特殊目标获得良好成像效果[6]。

逆时偏移思想提出之初，在叠后地震资料偏移成像中获得了良好的成像剖面[3]；但受限于计算机设备的发展，其巨大的计算量和存储I/O（输入/输出）成为其工业化应用的巨大瓶颈。随着计算机硬件设备的革新和GPU（Graphic Processing Unit）以及其编程架构CUDA（Computing Unified Device Archi⁃tecture）的快速发展，标量波动方程逆时偏移并行化算法已渐趋成熟[7-10]。但多分量地震资料联合逆时偏移的并行加速尚存在诸多问题，主要表现在：①多分量地震联合逆时偏移存储量和计算量远大于标量波动方程逆时偏移；②基于CPU/GPU协同并行的标量波动方程逆时偏移相关配套技术应用于弹性波逆时偏移尚需改进，如有效边界存储等。

目前的野外采集普遍向高密度、三维方向发展，为确保复杂构造观测波场的连续性，多采用小炮距、小接收线距、长排列接收，部分探区单炮记录过万道[11]。这导致三维弹性波逆时偏移过程中开辟的数组空间所占内存达10 G，依靠单节点GPU的加速不能满足存储需求。另一方面，在二维波动方程逆时偏移中为解决逆时延拓与正向延拓时间序列不一致性，常采用有效边界[12]存储正向延拓边界波场，实现正演波场的重构来保证与逆时延拓的时间一致性。但是在三维多分量地震资料联合逆时偏移中，需要保存的边界波场比之于二维情况增加数个数量级，加重了存储负担和存取I/O。

本文针对有效边界存储在三维情况下存储过大的情况，提出应用随机边界条件，在不保存边界波场的情况下，实现正向延拓波场的重构；考虑三维逆时偏移情况下，开辟数组空间内存较大，提出应用区域分解技术将计算数据分配到不同节点，实现基于MPI+CUDA的协同并行。

1 弹性波逆时偏移的基本原理

弹性波逆时偏移将多分量地震记录当作弹性波场的边值问题[13]来处理，由计算机实现炮点波场的正向延拓和接收点波场的逆时延拓，并在延拓过程中采用相应的算法实现纵横波的成像。其输入数据一般为未经坐标旋转的三分量炮集，输出数据一般包括反射纵波成像结果和转换横波成像结果。

弹性波逆时偏移的基本原理为：假定地下介质由一系列绕射点组成，地面、海底或井中接收到的三分量记录为各绕射点产生的纵横绕射波场在接收点处的叠加响应，其中各绕射点纵横绕射波的产生时间为炮点波场的主能量到达该点的时间[14]，绕射点产生的纵横绕射波振幅取决于该点的反射系数[15]，由此可通过求取各绕射点产生纵横绕射波的时间和该时刻的纵横波振幅来确定地下各绕射点的空间位置和反射系数，实现地下介质的纵横波成像。实际成像过程一般由以下几部分组成：①炮点波场的正向延拓和重构；②接收点波场的逆时延拓；③炮、检波场延拓过程中的纵横波解耦与横波的标量化处理；④纵横波成像。

1.1 一阶速度——应力弹性波方程及其高阶延拓差分格式

根据各向同性介质中，位移-应变关系、应力-应变关系、应力-位移关系[16]可推导得到各向同性介质中的一阶应力-速度弹性波方程：

其中，υx、υy、υz为质点振动速度；σxx、σyy、σzz、σxy、σxz、σyz为应力分量；ρ为密度；υp为纵波速度，υs为横波速度；x、y、z分别为空间坐标；t为时间。

在交错网格空间中对式（1）进行差分离散可得到时间2阶，空间任意偶数阶的差分格式，以式（1）中第一个方程为例：

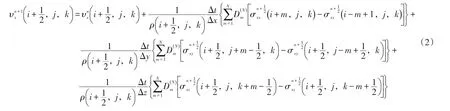
其中，Δx、Δy、Δz分别表示坐标系中x、y、z方向上的网格间距；Δt表示时间采样间隔；i，j，k分别代表x、y、z方向上离散点的序号；n表示时间上的离散点的序号。且ρ、μ半网格点上的值由同一方向上相邻整网格点求取算术平均得到。2N为差分阶数，D(mN)为2N阶交错网格差分系数，其计算公式为[16]：

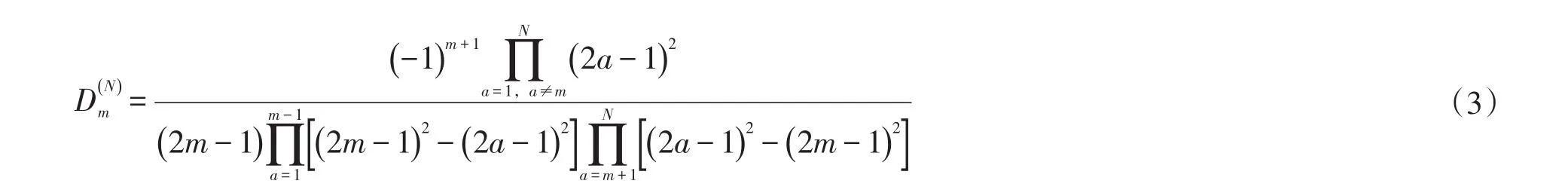
1.2 稳定性条件与吸收边界条件

弹性波方程交错网格有限差分格式属于显示差分型递推格式，计算当前时刻波场值时，需利用上一时刻波场值。由于数值计算截断误差的影响，随着时间递推误差会累积，破坏数值稳定性甚至引起计算溢出[17]。

通过对三维各向同性介质一阶双曲型弹性波方程进行平面谐波分析[16]可得稳定性条件为：

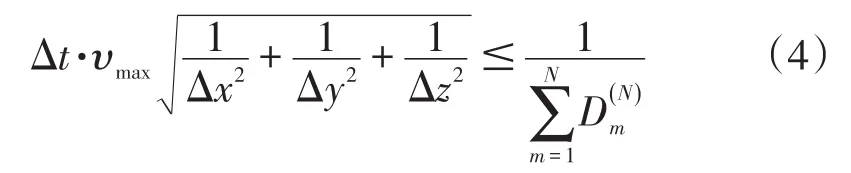
式（4）中，Δx、Δy、Δz分别表示坐标系中x、y、z方向上的网格间距；Δt表示时间采样间隔；υmax为背景纵、横波速度的极大值。对于三维各向同性弹性介质，地震波传播速度与传播方向无关，所以，在三个方向上的稳定条件相同。

采用无分裂式PML边界条件解决阶段边界的伪反射问题[18]，依据无分裂PML边界条件的实现思路，可得到式（1）基于无分裂PML边界条件的控制方程；以式（1）中第一个方程为例：

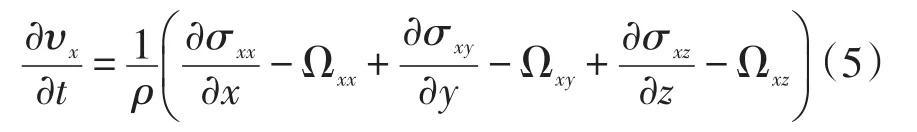
上式中Ωxx、Ωxy、Ωxz为引入的中间变量，其所对应的控制方程为：

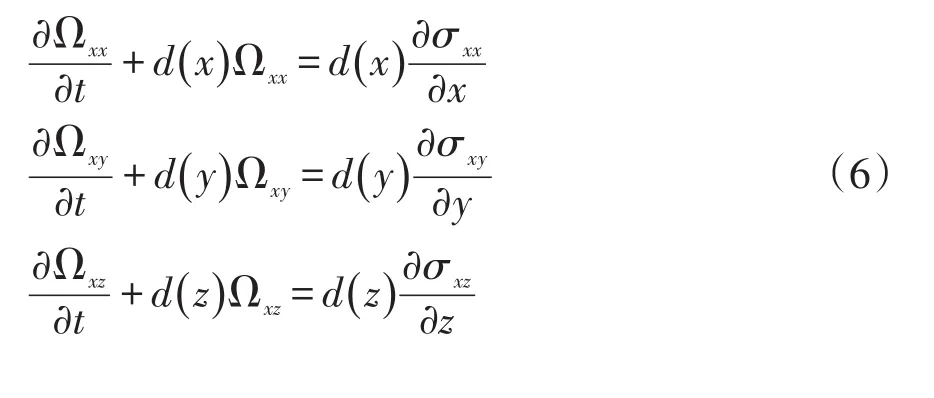
其中，d（x）、d（y）、d（z）为三个方向的衰减因子；根据公式（5）、（6）可依此类推基于无分裂PML边界条件的弹性波控制方程，其计算步骤为：（1）对包含PML边界的整个区域进行常规的弹性波波场求解；（2）在PML边界区域将得到的常规波场减去衰减量，然后按照时间轴方向更新辅助变量。由控制方程和计算步骤可知，无分裂的PML边界条件避免了对弹性波波场进行分裂，降低了存储。由于采用同一套方程也不会出现在边界处两套方程耦合的编程难题。

1.3 互相关成像条件

成像条件决定着逆时偏移成像剖面的质量。目前业界广泛应用互相关成像条件，其基本原理为：利用炮点波场和接收点逆时延拓波场做零延时互相关，在反射点位置的波场将得到加强，非反射点处的波场将削弱，最后所有时刻波场相加得到偏移剖面。互相关成像条件的实现算法为：

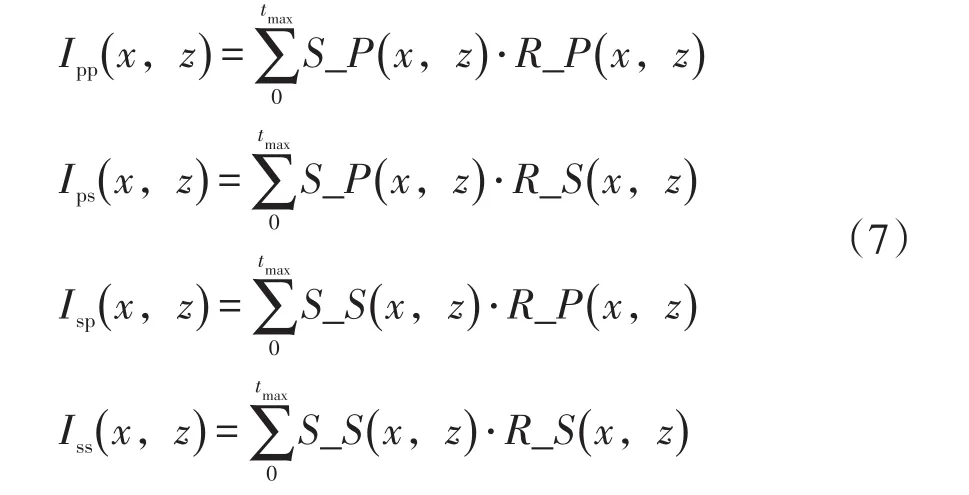
其中，Ipp（x，z）为PP波偏移剖面，Ips（x，z）为PS波偏移剖面，Isp（x，z）为SP波偏移剖面，Iss（x，z）为SS波偏移剖面，S_P（x，z）、S_S（x，z）为炮点纵、横波波场，R_P（x，z）、R_S（x，z）为接收点纵波和横波波场，纯纵横波波场的获得可参考文献[19，20]，tmax为地震记录长度。

2 基于多卡GPU的三维弹性波逆时偏移及其相关技术

上述弹性波逆时偏移基本流程中，在利用互相关成像条件时需同时应用相同时刻的检波点波场和炮点波场，上述两个波场的时间序列相反，因此需要重构炮点波场以实现纵横波成像；本文采用随机边界条件散射人工边界的伪反射，实现波场的重构。为了解决三维情况下单卡GPU显存不足的难题，利用区域分解技术将数据划分，实现大规模数据的三维弹性波逆时偏移。

2.1 随机边界条件的应用

在解决炮点、检波点波场时间序列不一致的问题中，国内外学者先后提出Checkpointing方法、有效边界存储策略[12]，来降低存储量。在二维弹性波逆时偏移中，有效边界存储策略已获得业界广泛认可；有效边界存储只需保存PML区域差分阶数层的边界值，即可实现波场的准确重构。但在三维情况下，其存存储量仍相当可观，假设三维模型网格点个数为200 m×300 m×400 m，采样点数为5 000，有限差分阶数为12阶，若采用有效边界存储其存储量达60G左右，这显然难以满足生成要求。因此，提出使用随机边界对波场进行散射[21]，因随机边界不涉及波场的衰减，其过程可逆，学者们提出“以计算换存储”，利用最后时刻波场即可重构得到每一时刻震源波场值。

随机边界条件实质为在计算区域外部随机赋速度值，利用随机速度的无规律性，将波场值散射，这样在进行互相关成像和叠加时，无规律的波场值能量得到减弱，反射点成像值相对得到增强。所以，随机边界条件的关键之处在于随机边界层内随机速度的选择，常用随机速度赋值公式为：

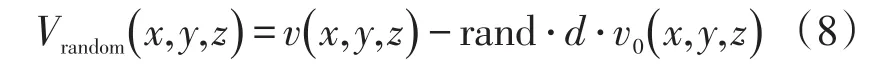
式中，Vrandom（x，y，z）为边界层内（x，y，z）处应取的随机速度，v（x，y，z）为对应的背景速度，rand是随机函数求得的随机数，d为随机边界层内的点（x，y，z）与区域边界的距离，v0（x，y，z）为最大稳定速度。

为了验证随机边界条件的适用性，本文采用二维均匀速度模型，验证随机边界的重构和散射效果。二维均匀速度模型大小1500 m×1500 m，纵波速度为2500 m/s，横波速度1800 m/s，炮点位置位于（750 m，750 m），纵波源激发，记录不同时刻vz分量的正演和重构波场快照。图1即为均匀介质随机边界速度场，图2、图3、图4即为不同时刻正向延拓和逆时重构的波场值，由此可验证随机边界的有效性及波场重构的正确性。

2.2 区域分解技术及基于MPI+CUDA的弹性波逆时偏移流程

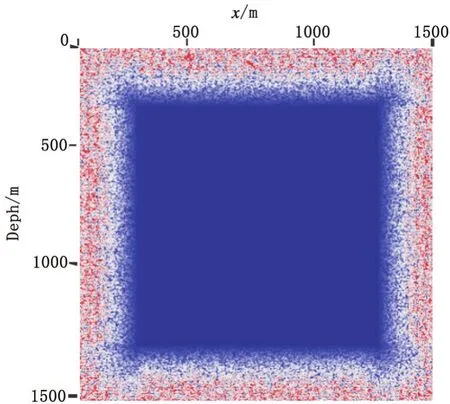
图1 二维均匀介质随机边界速度场Figure1 2D homogeneous medium stochastic boundary velocity field

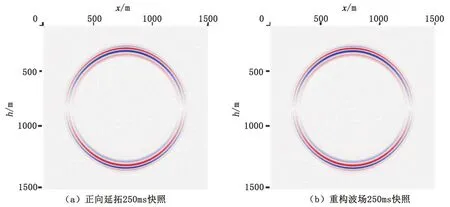
图2 二维均匀介质随机边界正向延拓（250 ms）及重构波场快照Figure 2 2D homogeneous medium stochastic boundary forward continuation（250 ms）and wave field reconstruction snapshot

GPU中有大量晶体管，是专为执行复杂的数学和几何计算而设计的。当今的GPU已不再将这些计算局限于图形渲染，其通用计算技术的发展和天生的并行处理机制在计算方面提供了高于CPU数十倍乃至上百倍于CPU的性能。业界已经利用GPU的并行特性在二维逆时偏移取得了一系列突破[22-24]，然而对于大规模数据处理通常需要较大的计算机内存（显存），GPU目前的显存一般为6～8 G，对于模型较大和实际数据的三维逆时偏移这显然是不能满足计算要求，需要进行特殊情况考虑。本文的解决策略为将地震数据进行区域分解[10]，形成多GPU协同处理单炮地震数据的快速计算方法；此方法在理论上可以对任意规模的三维地震资料进行逆时偏移成像。

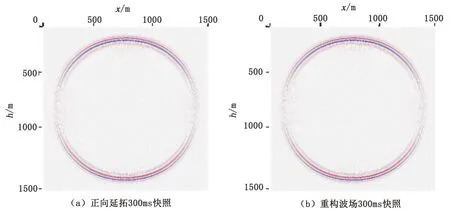
图3 二维均匀介质随机边界正向延拓（300 ms）及重构波场快照Figure 3 2D homogeneous medium stochastic boundary forward continuation（300 ms）and wave field reconstruction snapshot

图4 二维均匀介质随机边界正向延拓（350 ms）及重构波场快照Figure 4 2D homogeneous medium stochastic boundary forward continuation（350 ms）and wave field reconstruction snapshot

在对弹性波方程的差分格式，进行有限差分计算编程时，将一个维度上（以y方向为例）的区域进行划分，按照实际资料的大小和显卡显存的限制来决定划分的数量。利用区域分解进行差分计算，需要解决的核心问题在于如何隐藏卡与卡间的数据交换。如图5所示，为了保证差分计算的正确性，在每一个时间步需要在虚线区域进行数据交换。

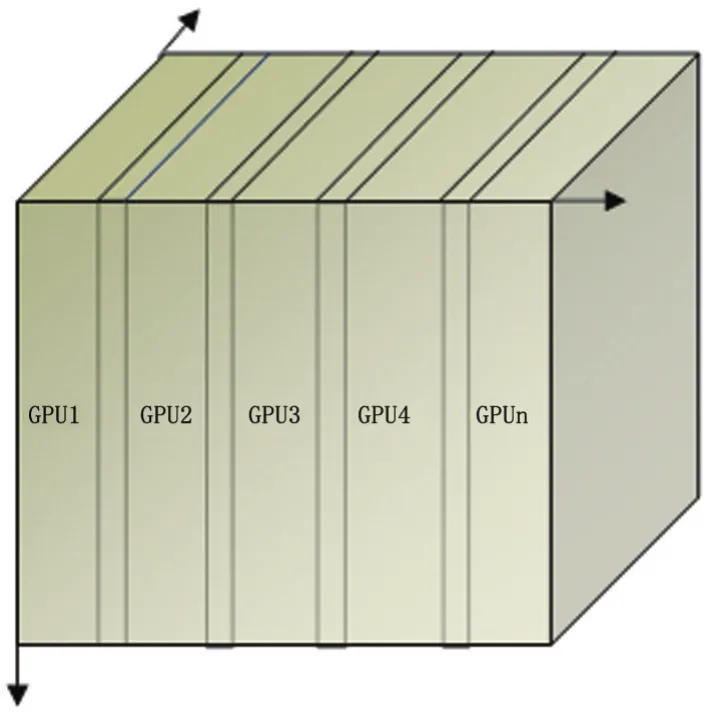
图5 三维数据体区域分解示意图Figure 5 A schematic diagram of 3D data volume domain decomposition

以其中的两块卡为例，说明分解区域后每块卡的计算与数据传递。如图6所示，每块卡可以分为三部分（图中分别用A、B和C表示），C区域为两块卡之间的重叠部分，厚度由差分格式来决定，B区域为传递部分与C区域保持一样的厚度，A区域为显卡本身的计算区域。在正演和延拓计算的每一个时间步内，C区域的网格处在边界而无法进行差分运算，所以需要将B区域的数据传递到C。这样计算过程就分为了如下步骤：首先是每块卡计算B区域；然后，每块卡计算A区域的同时，传递B区域数据到相邻显卡。

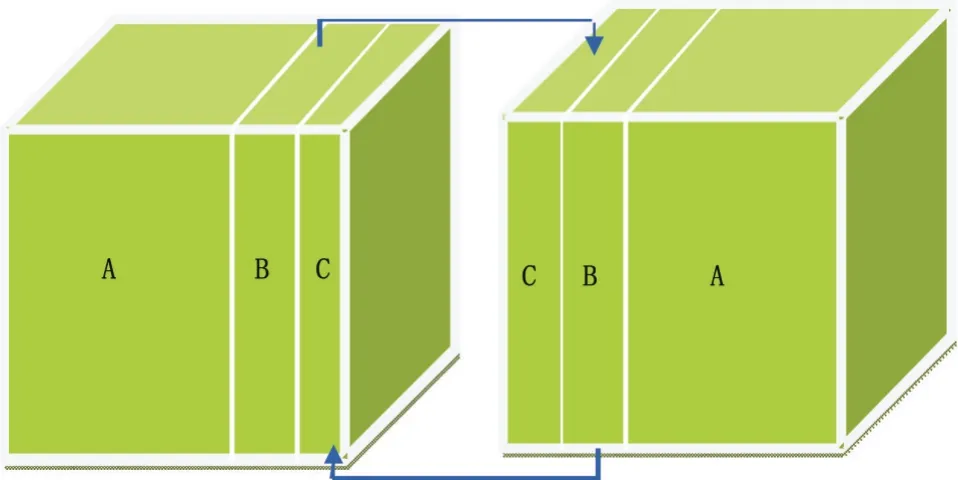
图6 区域分解数据交换示意图Figure 6 A schematic diagram of domain decomposition data exchange

计算能力高于2.0的NVIDIA显卡支持在同节点上进行显卡与显卡之间的数据交换。而本文提出的多卡并行是基于多节点的并行，在数据传递时需要将传递数据通过内存中转传递，由MPI的每一个进程控制每块显卡，在MPI进程组内进行非阻塞的数据交换。整个的实现流程图如图7所示：①由主进程读取到炮记录和速度模型并分发于进程；②各进程控制GPU显卡实现每一时间步的图4B区域波场计算；③GPU回传数据并在内存中交换，同时实现图4A区域的波场计算；④循环迭代波场，最后由主进程规约得到最终的偏移结果。

3 数值算例

SEG/EAEG盐丘模型是一个国际上通用测试三维复杂构造成像效果的地质模型。本文采用SEG/ EAEG盐丘速度模型作为纵波模型，通过固定的纵横波速度比构造横波模型，炮集记录由一阶弹性波方程有限差分正演获得。模型参数如下：模型大小3380 m×3380 m×1050 m，网格大小Δx=Δy=Δz=5 m，时间采样间隔0.35 ms，记录长度2.8 s，震源为35 Hz雷克子波。观测系统参数为：总炮数4690炮，67条测线，炮线间距50 m，炮间距60 m，接收线间距10 m，接收道间距5 m，每条测线70炮，每炮30400道接收；偏移算法采用本文所提出的基于MPI+CUDA的三维弹性波逆时偏移并行算法。图8为三维盐丘模型的纵横波速度模型以及多分量逆时偏移剖面。

另外，PP、PS的成像效果较SP、SS的成像效果更好。原因为：PP，PS波是在纵波倾斜入射到弹性界面时产生能量较强，而SP、SS是由纵波倾斜入射到弹性界面产生的转换横波再次入射得到的地震记录，该情况涉及波型的多次转换，情况复杂。因此PP成像结果主要代表了P波的反射系数，PS主要成像结果代表了PS波的反射系数；而SP、SS成像结果并不对应一种波的反射系数，多次转换后并不清楚它的能量分布。PP波和PS波均可以对盐丘模型构造得到准确的偏移成像结果。PP波主频比PS波主频低，其原因在于：模型资料的纵横波记录是由同一纵波源激发得到，且转换横波在空间域中的波长小于纵波波长，所以在模型资料的深度偏移成像结果中PS成像结果分辨率高于PP成像结果。

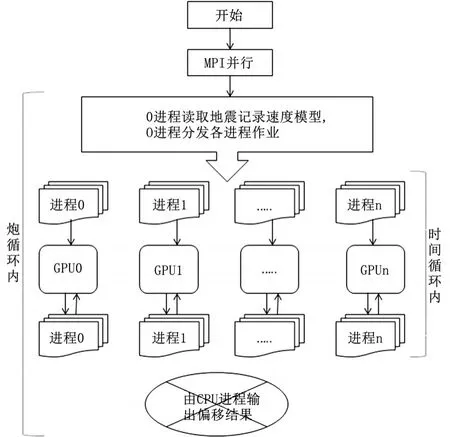
图7 三维弹性波逆时偏移协同并行流程图Figure 7 3D elastic wave RTM cooperative parallel flow chart

4 结论

随机边界条件在不保存边界波场的情况下，可以实现正向延拓波场的逆时重构，避免了三维弹性波逆时偏移大规模的边界存储问题；区域分解技术的应用使得大规模数据资料的逆时偏移处理成为可能；在上述基础上，本文提出的基于MPI+CUDA协同并行的三维弹性波逆时偏移方法可以对模型资料准确成像。

[1]Gaiser J，Strudley A.Acquisition and application of multicomponent vector wavefields：are they practical[J].first break，2005，23(6)：61-67.

[2]Whitmore，N.D.Iterative depth migration by backward time propaga⁃tion.1983 SEG Annual Meeting.Society of Exploration Geophysicists，1983.

[3]McMechan G A.Migration by extrapolation of time-dependent bound⁃ary values.Geophysical Prospecting，1983，31(3):413-420.

[4]Baysal E，Kosloff D D，Sherwood J W C.Reverse time migration.Geo⁃physics，1983，48(11):1514-1524.

[5]Loewenthal D，Mufti I R.Reverse time migration in the spatial fre⁃quency domain.Geophysics，1983，48(5):627-635.

[6]杨佳佳.多分量地震波逆时偏移的关键技术研究[D].中国海洋大学，2015.

[7]何兵寿，张会星，韩月.双程声波方程叠前逆时深度偏移及其并行算法.煤炭学报，2010，35(3)：458-462.

[8]李博，刘国峰，刘洪.地震叠前逆时偏移的一种图形处理器提速实现方法[J].地球物理学报，2009，52(12)：245-252.

[9]刘红伟，李博，刘洪等.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报，2010，53(7)：1725-1733.

[10]刘守伟，王华忠，陈生昌，等.三维逆时偏移CPU/GPU机群实现方案研究[J].地球物理学报，2013，56(10).

[11]唐祥功，匡斌，杜继修.多GPU协同三维叠前逆时偏移方法研究与应用：石油地球物理勘探，2013，48（6）：910-914

[12]王保利，高静怀，陈文超等.地震叠前逆时偏移的有效边界存储策略[J].地球物理学报，2012，55(7):2412-2421.

[13]Chang，W.F，McMechan G A.Elastic reverse-time migration[J].Geo⁃physics，1987，52(10)：1365-1375.

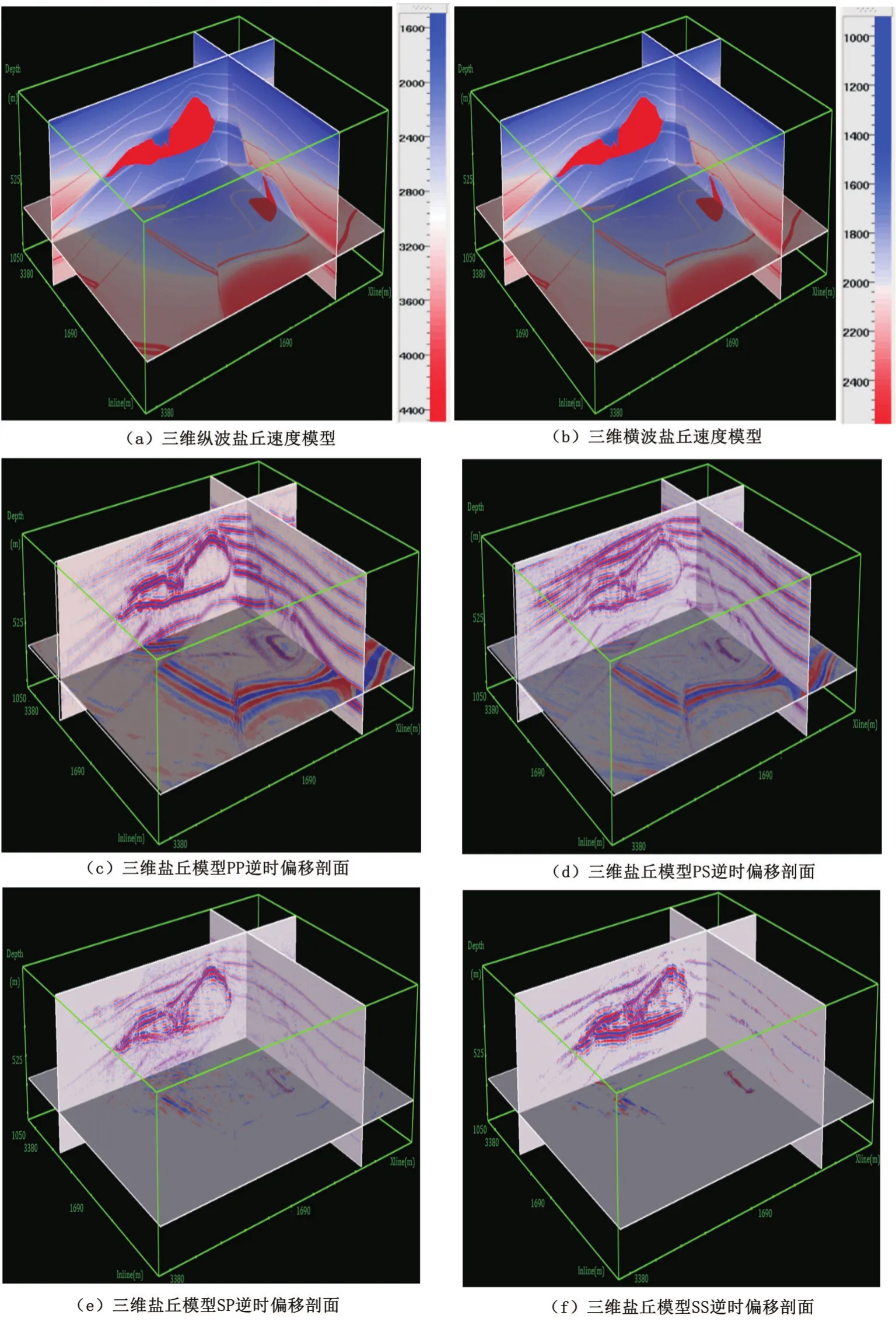
图8 三维弹性波速度模型及逆时偏移成像结果Figure 8 3D elastic wave velocity model and RTM imaging result

[14]Claerbout，J.F.Toward a unified theory of reflector mapping[J].Geo⁃physics，1971，36(3):467-481.

[15]Zhi L，Chen S，Li X.Joint AVO inversion of PP and PS waves using exact Zoeppritz equation[M]//SEG Technical Program Expanded Ab⁃stracts 2013.Society of Exploration Geophysicists，2013：457-461.

[16]牟永光，裴正林.三维复杂介质地震数值模拟[M].北京:石油工业出版社，2005，173-176.

[17]董良国，马在田，曹景忠.一阶弹性波方程交错网格高阶差分解法稳定性研究[J].地球物理学报，2000，06:856-864.

[18]王鹏飞，何兵寿.声波方程逆时偏移中的无分裂PML吸收边界条件[J].工程地球物理学报，2015，12(5):583-590.

[19]Dellinger J，Etgen J.Wave-field separation in two-dimensional anisotropic media.Geophysics，1990，55(7)：914-919.

[20]Du Q Z，Gong X F，Zhang M，et al.3D PS-wave imaging with elastic reverse-time migration.Geophysics，2014，79(5)：S173-S184.

[21]Robert G.Clapp.Reverse time migration with random boundar⁃ies.79th Annual International Meeting，SEG Expanded Abstracts，2009，28：2809-2813.

[22]Micikevicius P，3D finite difference computation on GPUs using CU⁃DA.//Processing of 2th Workshop on General Purpose Processing on Graphics Processing Units，Expanded Abstracts，2008:79-84.

[23]Michea D，Komatitsch D，Mahovsky J，et al.Industrial-scale reverse time migration on GPU hardware.SEG Expand Abstracts，2009:2789-2793.

[24]Sun X Y，Suh S.Maxing throughput for high performance TTI-RTM: From CPU-GPU.SEG Expanded Abstracts，2011，182(1):389-402.

Application of Multi-card GPU in 3D Elastic Wave Reverse-time Migration(RTM)

Shen Jiqian
(Jiangsu Provincial Coal Geological Exploration,Geophysical Prospecting and Surveying Team,Nanjing,Jiangsu 210046)

With the increasing complexity of seismic exploration objects,higher requirements are put forward on imaging results.The RTM can be used to describe complex structures in theory.A series of research findings have been acquired in 2D RTM;however,the huge amount of storage,computational workload and field single-shot data in RTM have become the bottleneck to restrict its applica⁃tion in 3D multi-component data.In allusion to the issue of larger efficient boundary storage in 3D RTM,the stochastic boundary ap⁃proach is used to lower down RTM storage and improve migration efficiency.This boundary condition needs not to keep wave field val⁃ue of components at boundary and realize reverse-time reconstruction.Whereas 3D RTM needs larger array space in computation,the author applies the domain decomposition technique to distribute computational data to different nodes and realize cooperative parallel based on MPI+CUDA.The SEG/EAGE salt dome example has proved the effectiveness of the method.

3D elastic wave RTM;stochastic boundary;domain decomposition;MPI+CUDA cooperative parallel

P631.4

A

10.3969/j.issn.1674-1803.2017.03.14

1674-1803(2017)03-0065-07

国家自然科学基金（41674118），国家重大科技专项（2016ZX05027-002）联合资助

沈骥千（1970—），男，高级工程师，主要从事地震勘探资料处理工作。

2017-02-10

责任编辑：孙常长