浅谈桥梁索力动测仪不确定度分类与计算方法

（重庆交通大学 400074）

浅谈桥梁索力动测仪不确定度分类与计算方法

王荣川

（重庆交通大学 400074）

对引起索力动测仪不确定度的各种因素进行分析，提出了索力动测仪不确定度的量化方法，对各种影响因素进行了详细的分类。

不确定度； A类评定；B类评定；重复性；稳定性

1.前言

测量不确定度可分为标准不确定度和扩展不确定度，标准不确定度的分为A类标准不确定度和B类标准不确定度A类标准不确定度和B类标准不确定度合成叫做合成标准不确定度，扩展不确定度可分为包含因子k=2、3情况和p为包含概率的情况

2.索力动测仪不确定度的分类与计算

分析索力动测仪不确定度来源及其评定是对其进行不确定度计算的前提，本项目在室温（10～35）℃，校准过程中温度波动不大于2℃的测量环境下，将锚索测力计（压力环）视为标准装置，将《索力动测仪校准规范》适用的索力动测仪视为被校对象，基于弦振动理论，利用加速度传感器拾取被测对象的随机振动信号，通过信号采集分析仪识别其各阶振动固有频率，根据拉力与振动固有频率之间的对应函数关系，得到实测拉力。

（1）不确定度计算假设

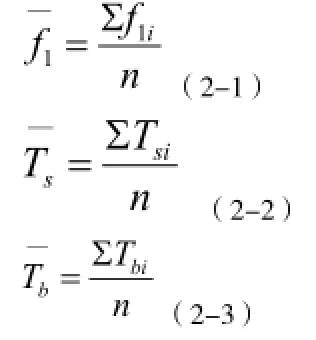
（2）不确定计算模型

数学模型为：

式中：δ—索力动测仪示值误差；

合成标准不确定度评定模型

故1-4公式可简化为：

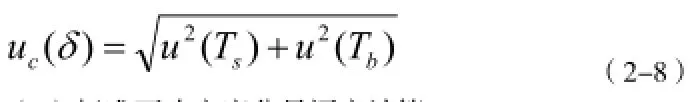
（3）标准不确定度分量评定计算

1）标准装置传递引起的不确定度

由调研可知，压力环精准度为0.5%，允许偏差为：

则由此产生的不确定度为：

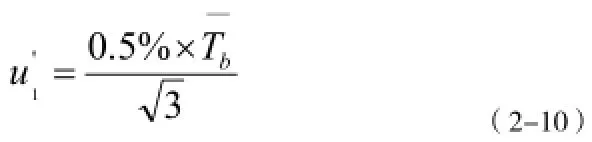
相对不确定度：

2）索力动测仪测量模型参数传递所带来的不确定度

① m引起的不确定度

② L引起的不确定度

③ f1引起的不确定度

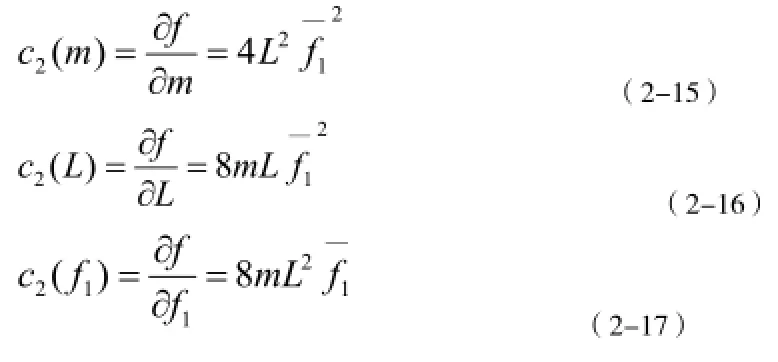
由合成标准不确定度得：

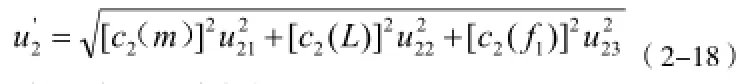
则相对标准不确定度：

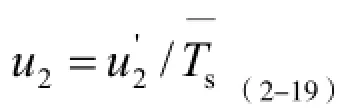
3）偏移引起的不确定度

用B类不确定度评定，假设其均匀分布：

则相对标准不确定度：

4）重复性引起的不确定度

重复性引起的标准不确定度：

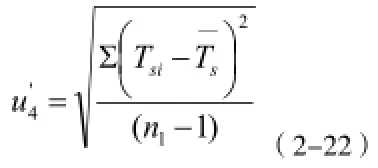
重复性引起的相对标准不确定度：

5）稳定性引起的不确定度

设连续四年对索力动测仪进行复校，每年得到的索力动测仪示值平均值分别为则连续四年的示值平均值的平均值为：

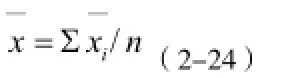
稳定性引起的标准不确定度为：

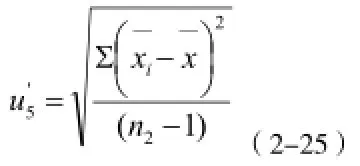
稳定性引起的相对标准不确定度为：

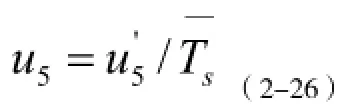
6）复现性引起的不确定度

设分别由三人对索力动测仪进行校准试验，分别得到索力动测仪示值平均值为

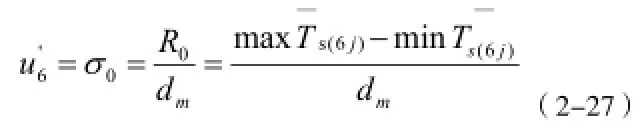
相对标准不确定度为：

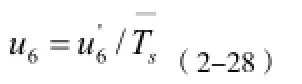
表2-3 极差系数表

由上结果可计算合成相对标准不确定度为：

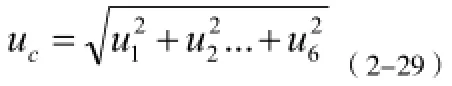
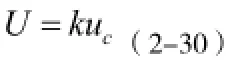
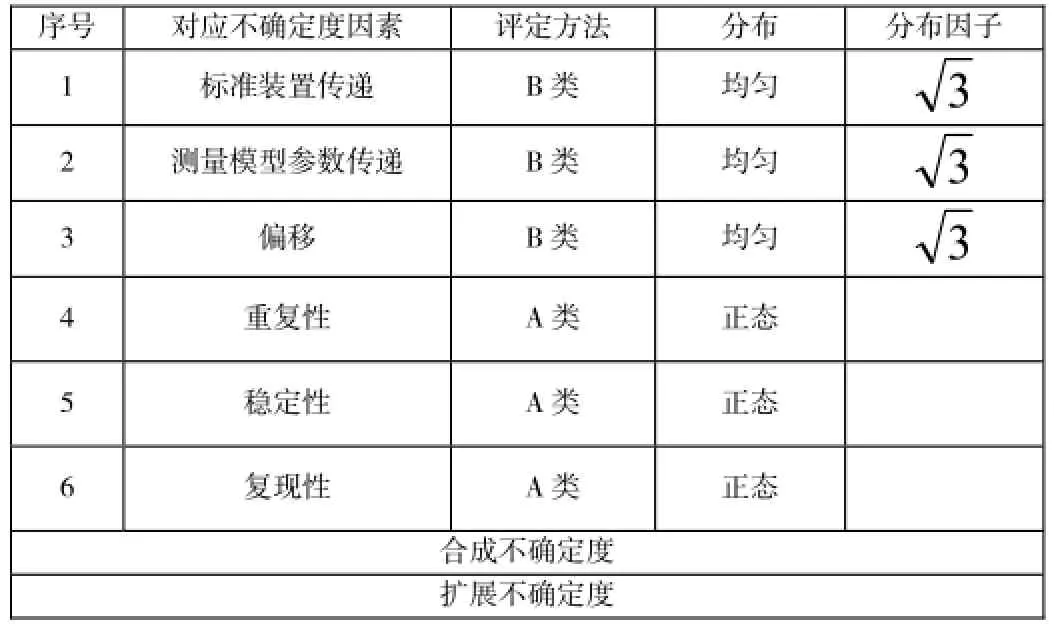
表2-4 不确定度来源与计算简表

3.结论

针对索力动测仪不确定度分类与计算，学习了不确定度评定方法，并与拉索测试的实际工程相结合。总结出适用于索力动测仪的不确定度分类与计算，并将其进行更加严谨的分类，使其更加通俗易懂，例如：不确定度来源可分为与真值直接相关的来源和与真值不直接相关的来源两大类，并将所有可能的不确定度都罗列到所给出的不确定度来源里，更加深入的了解了偏移对应的不确定度。在对索力动测仪进行不确定度评定后，发现拉索的单位长度质量所产生的不确定度分量占总不确定度相当大的份额，所以在拉索生产时需严格控制其单位长度质量的误差，以减少索力动测仪不确定度和工程安全问题。

[1]郑罡，倪一清，高赞明，徐兴. 斜拉索张力测试和参数评估的理论和应用[J].土木工程学报，2005，03：64-69.

[2]李东旭，高等结构动力学[M].科学出版社，2010.9.

[19]Irvine H. Max. Cable Structure[J]. 1981.

[3]Elsa de Sá Caetano E. Cable vibrations in cable-stayed bridges[M]. IABSE，2007.

[4]Casas J R. A combined method for measuring cable forces： the cable-stayed Alamillo bridge， Spain[J]. Structural Engineering International， 1994， 4(4)： 235-240.

[6]顾龙方, 陈意华, 宋明顺. 计量学的新进展[J]. 中国计量学院学报, 2002, 13(4)： 270-273.

[7]邵长江,喻梅,振动法测斜拉索索力[J],四川建筑,2003(01).

[8]李东升，计量学基础[M]，机械工业出版社，2014.

U45

B

1007-6344（2017）04-0052-02