基于自然电位计算泥质砂岩储层孔隙度的方法

2017-04-24任杰翟芳芳李风玲陈彬

测井技术 2017年3期

任杰, 翟芳芳, 李风玲, 陈彬

(中石化中原油田分公司勘探开发研究院, 河南濮阳 457001)

0 引言

阿根廷EH油田主要含油层系为Chubut群Canadon Seco/Bajo Barreal组,主要为陆相河流相沉积,砂体分布不稳定,横向变化快,连续性差。该油田大部分井采用的测井系列仅有自然电位、冲洗带电阻率和深感应电阻率3条曲线,传统技术中利用这3条曲线仅能够实现储层厚度粗略划分和储层渗透性好坏的定性评价,但油藏地质建模和老井挖潜等方面的研究工作对这些井的储层孔隙度、渗透率、饱和度提出了连续定量解释的需求。

常规测井解释中,孔隙度的定量计算往往采用密度、声波时差和补偿中子三孔隙度曲线的理论孔隙度模型,或结合岩心分析建立区域经验孔隙度模型[1],而目前EH油田只有很少量的井测取声波时差曲线,测井资料综合定量评价遇到了困难。基于此,本文通过研究EH油田的储层特征,利用EH油田有限的测井曲线,优选出对孔隙度敏感的曲线,构建孔隙度定量计算模型,并利用传统方法对孔隙度计算结果进行验证,为油藏精细评价提供可靠的储层参数。

1 孔隙度敏感曲线优选

EH油田目的层段为河流相的泥质砂岩储层,实验室取心电镜分析表明,目的层段的泥岩完全分散在砂岩之中,部分充填了粒间孔隙或包敷于砂岩颗粒,为分散状泥质。

斯伦贝谢公司把泥质在砂岩中的分布形式归纳为3种类型:分散泥质、层状泥质和结构泥质,层状泥质和结构泥质并不影响砂岩的孔隙度、渗透率,而分散泥质使砂岩的有效孔隙度和渗透率明显降低[2]。因此,EH油田的储层中砂岩的泥质含量越大,对应储层的孔隙度就越小,渗透率也就越低,即孔隙度与泥质含量理论上应成负相关关系。利用自然电位计算泥质含量的公式为[3]

(1)

(2)

式中,ESP为自然电位测井值,mV;ESP,max为纯泥岩处的自然电位测井值,mV;ESP,min为纯砂岩处的自然电位测井值,mV;Ish为自然电位相对值;GCUR为希尔奇(Hilchie)指数;Vsh为泥质含量,小数。由式(2)可以看出,泥质含量和自然电位相对值为正相关关系,而孔隙度和泥质含量为负相关关系,即孔隙度和自然电位相对值理论上为负相关。

利用EH油田储层段7口取心井计算的自然电位相对值与对应92个岩心分析孔隙度作交会图(见图1),图1中交会关系的相关系数R为0.730 7,表明岩心分析孔隙度与自然电位相对值有较好的负相关关系。因此,自然电位曲线可作为建立孔隙度计算模型的1条敏感曲线。

统计表明,EH油田各井储层段埋藏深度范围比较大,约为1 000～3 000 m,理论上属正常压实地层,随着埋藏深度的增加,受到上覆地层压力的影响,孔隙度有一定的减小趋势[4],因此建立埋藏深度和对应92个岩心分析孔隙度的交会关系图(见图2)。图2中交会关系的相关系数R为0.771 5,表明孔隙度和埋藏深度也有较好的负相关关系,测井深度曲线也可作为建立孔隙度计算模型的1条敏感曲线。

除此之外,理论上冲洗带电阻率一定程度上也能够反映储层泥浆横向侵入深度的大小,与储层孔隙度有一定的关系,但冲洗带电阻率经常受钻井过程、泥浆状况和地层条件等因素的影响,在储层中的冲洗带电阻率比较复杂多变,在EH油田取心井中,通过作冲洗带电阻率Rxo和对应92个岩心分析孔隙度φ的交会关系图(见图3),图3反映孔隙度和冲洗带电阻率的相关关系差,因此,在EH油田,不能将冲洗带电阻率曲线作为建立孔隙度计算模型的敏感曲线。

图3 冲洗带电阻率和岩心分析孔隙度交会关系图

2 孔隙度计算模型

2.1 自然电位的层厚校正

测井中自然电位曲线的纵向分辨率为4 m,当储层厚度小于4 m时,自然电位曲线受围岩、泥浆侵入等因素的影响,由实测自然电位计算的自然电位相对值比储层真实自然电位相对值大,且储层越薄,由实测自然电位计算的自然电位相对值越大,求取的泥质含量就越大。因此,在求取储层泥质含量之前,要对自然电位曲线做层厚校正处理,利用斯伦贝谢公司给出的地层自然电位校正图版[5],首先确定出储层各采样点对应的围岩电阻率Rs、泥浆电阻率Rm、冲洗带电阻率Rxo、深感应电阻率Rt、地层厚度h、井径dh、自然电位值ESP,然后查图版确定出储层段各采样点对应的校正后的自然电位ESP,cor。

2.2 孔隙度计算模型的构建

由上述分析可知,孔隙度与泥质含量、埋藏深度在EH油田储层段都有一定负相关关系,因此,孔隙度模型可构建为以泥质含量和埋藏深度为自变量的二元关系表达式。

图4 孔隙度二元模型交会图

首先在EH油田取心井储层段92个采样点,用上述自然电位的层厚校正方法得到校正后的自然电位ESP,cor,由式(1)和式(2)计算对应的泥质含量Vsh,然后采用岩心孔隙度刻度法和多元拟合方法建立岩心分析孔隙度φ和泥质含量Vsh、埋藏深度D的二元交会关系,运用异常点剔除技术,最终应用84个采样点建立了孔隙度φ的二元模型(见图4),该二元模型表达式为

φ=-0.0031D-21.7115Vsh+28.8071

(3)

相关系数R为0.825 0,表明该孔隙度模型相对可靠。

通过作岩心分析孔隙度和二元模型计算孔隙度的交会图(见图5),取心点基本上都落在对角线附近,相对误差控制在±5%以内,这在有限的测井资料条件下达到了相对理想的效果。

图5 岩心分析孔隙度与二元模型计算孔隙度交会图

3 方法可靠性验证

3.1 声波时差验证

在EH油田选取测井系列中同时包含声波时差和自然电位曲线的A井和B井,读取能够反映储层段特征的32个采样点对应的声波时差,利用研究区已有的声波时差计算孔隙度的经验模型计算对应的孔隙度φΔt

φΔt=0.6102Δt-31.597

(4)

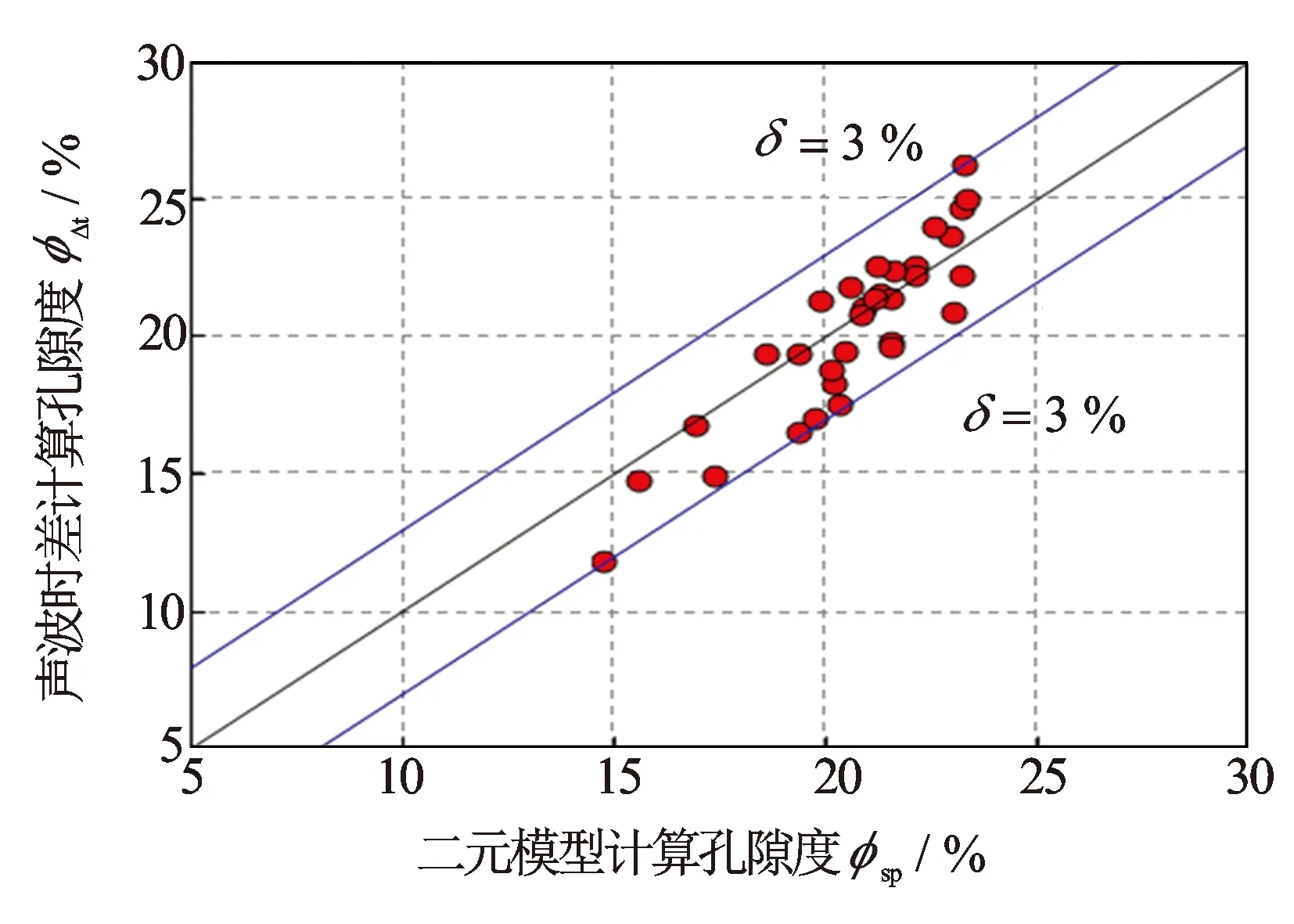
图6 二元模型计算孔隙度与声波时差计算孔隙度交会图

式中,Δt为声波时差测井值。利用声波时差计算的孔隙度φΔt与利用式(3)计算的孔隙度φsp作交会图(见图6)。图6中2种方法计算的孔隙度基本上都能够落在对角线附近,相对误差小于±3%。

为了实现各井储层的连续处理,根据史金安等[6]的自然电位校正图版量化方法,编制对应的自然电位校正程序,然后进行测井综合解释。图7是B井1 895～1 950 m井段测井综合解释成果图。图6中第2道蓝色曲线即为校正后的自然电位曲线,第5道红色曲线是利用本文构建的二元孔隙度计算模型计算的孔隙度,蓝色曲线是声波时差求取的孔隙度。2种方法得到的孔隙度曲线具有很好的一致性,表明该二元孔隙度计算模型实用性好。