新型随钻电磁波阵列补偿传播电阻率测井仪器性能仿真

马明学, 毛保华, 岳喜洲, 刘保银, 张中庆,3

(1.中海油服油田技术研究院, 河北 燕郊 065201; 2.杭州迅美科技有限公司, 浙江 杭州 310012; 3.浙江大学, 浙江 杭州 310012)

0 引 言

20世纪90年代Schlumberger、Halliburton和Baker Hughes等公司相继推出了补偿型、阵列型随钻电磁波测井仪器,如Schlumberger公司的ARC系列[1-2]、Halliburton公司的EWR系列[3]、Baker Hughes公司的MPR系列。在国外,随钻电磁波电阻率测井已成为随钻测井的必测项目,但中国仍处于研究发展阶段[4]。2015年中海油田服务股份有限公司推出了1套自主研制的随钻电磁波阵列补偿传播电阻率仪ACPR(Array Compensation Propagation Resistivity),该仪器可提供8种不同探测深度的相位差电阻率和幅度比电阻率,已在生产测井中得到广泛的应用。在实际测井中,因对仪器探测性能和各种测量环境的影响缺乏一定的认识和理论支持,为后续测井解释和地层评价带来一定的困扰。

本文基于矢量有限元素法理论[5-6],结合ACPR仪器结构参数和工作原理,开发了三维矢量有限元素法正演仿真软件,通过与第三方软件COMSOL[7]仿真结果对比验证了算法的正确性。在此基础上考察了ACPR仪器的探测特性以及各种环境因素的影响,包括仪器探测深度、纵向分层能力以及井眼环境影响、地层各向异性影响等,为后期资料处理解释和地层评价奠定了理论基础。通过搭建实验平台构造地层模型,对比仪器测量结果与软件模拟结果,各深度点相对误差均小于5.0%。渤海某口勘探井实测数据对比表明,ACPR随钻电阻率和电缆双侧向电阻率具有较好的一致性,即使在高电阻率层段,随钻相位差电阻率和电缆深侧向电阻率数据也基本一致,显示该仪器较好的可靠性和广泛的适用性。

1 仪器简介及基本理论

1.1 仪器简介

图1是ACPR仪器结构示意图。采用阵列线圈系以改善仪器径向探测特性,该线圈系由2对对称的发射线圈T1和T2,中间夹2个接收线圈R1和R2。采用2 MHz和400 kHz这2种工作频率,测量接收线圈R1和R2上的电压信号,通过线圈补偿及信号转化处理,可实现8种不同探测深度的测量曲线,包括2种频率2个源距的相位差和幅度比电阻率。

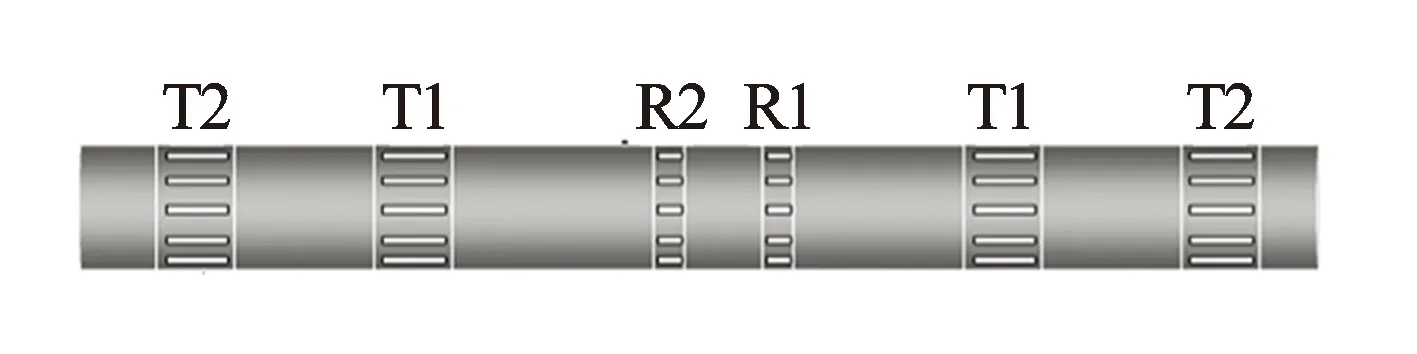
图1 ACPR仪器结构示意图

1.2 基本理论

随钻电磁波阵列补偿传播电阻率测井理论可归结为求解给定边界条件下的麦克斯韦(Maxwell)方程问题[8-10]。地球物理问题中的电磁场满足Maxwell方程(1)

(1)

式中,E表示电场强度;J为源电流密度;ω为源电流角频率;σ为电导率;μ为磁导率。从Maxwell方程出发,可以推导出电场所满足的矢量波动方程为

(2)

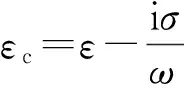
令E=Ep+Es

(3)

式中,背景场Ep是当全部空间被电导率为σ0的介质填充时的电场,其满足方程

(4)

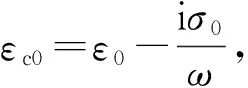
(5)

背景场Ep可通过解析方法计算得到,二次场Es则由有限元素法计算。相对于式(2),式(5)的解变化平缓,可以利用稀疏一些的网格进行求解,减少计算工作量。选取足够大区域,使边界上的电场衰减到近似为0,则式(5)只需满足边界条件(6)

n×E|∂Ω=0

(6)

式中,∂Ω为求解区Ω的边界;n为其法线方向。

考虑式(6),将矢量波动方程(5)转化为其弱积形式

(7)

式中,N为矢量基函数。

2 软件正确性验证

基于上述理论指导,开发了矢量有限元素法三维正演仿真软件,用于ACPR仪器响应分析。在无限厚均匀地层模型参数下,通过与第三方软件COMSOL仿真结果进行对比,验证了仿真程序的正确性。本文中曲线命名规则说明:R表示视电阻率;PS表示相位差;AD表示幅度比;H表示2 MHz频率;L表示400 kHz频率;最后一位字母代表源距;S表示短源距;L表示长源距。如,PSHL表示长源距2 MHz相位差,RPSHS表示短源距2 MHz相位差视电阻率。

表1 2种软件仿真结果对比表

表1中的数据均为经过空气吊零后的结果,通过不同地层电阻率下2种软件仿真结果的对比可知,低电阻率区(电阻率小于100 Ω·m)各曲线相对误差均小于5%;高电阻率区(电阻率1 000 Ω·m)相对误差虽然大于5%,但两者的绝对误差很小,表明所开发的数值模拟软件的准确性,为后续复杂模型下仪器探测特性的考察奠定了坚实的基础。

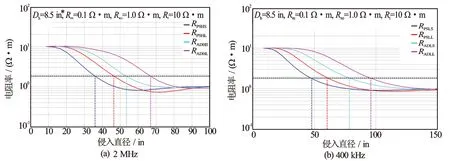
图2 不同频率下泥浆侵入对ACPR测井响应的影响图*非法定计量单位,1 in=2.54 cm,下同

3 仪器性能及环境影响

3.1 径向探测深度

ACPR仪器的探测深度用图2的泥浆侵入影响图表示。图2表示无限厚地层模型下随着泥浆侵入深度不断加深,ACPR仪器不同频率和不同源距下相位差和幅度比电阻率的测井响应变化规律。随着泥浆侵入的加深,不论是高频模式还是低频模式测量曲线均出现一定的分离,其可作为测井解释中泥浆侵入判断依据。

本文采用伪几何因子的方法来定义仪器的径向探测深度,定义伪几何因子等于0.5时所对应的泥浆侵入深度为仪器的径向探测深度。在泥浆侵入带电阻等于1.0 Ω·m、地层真电阻率等于10.0 Ω·m时,当伪几何因子等于0.5时,仪器的测量响应等于1.8 Ω·m,对应于图2可知ACPR仪器的探测深度(见表2)。幅度比的径向探测深度要比相位差的探测深度深,源距越大径向探测深度越深,工作频率越低径向探测深度越深。

表2 ACPR径向探测深度表(探测深度按侵入半径计算)

3.2 纵向分层能力

为了考察ACPR仪器的分层能力,模拟了不同层厚2 MHz[见图3(a)]和400 kHz[见图3(b)]2种工作频率下不同源距的相位差和幅度比电阻率响应规律。随着层厚的减小,仪器的测量响应值逐渐偏离地层真值,且表现出幅度比比相位差衰减得更快、长源距比短源距衰减得快、低频比高频衰减得快等规律,反映到仪器的分层能力上即相位差高于幅度比、短源距高于长源距、高频大于低频(见图3)。

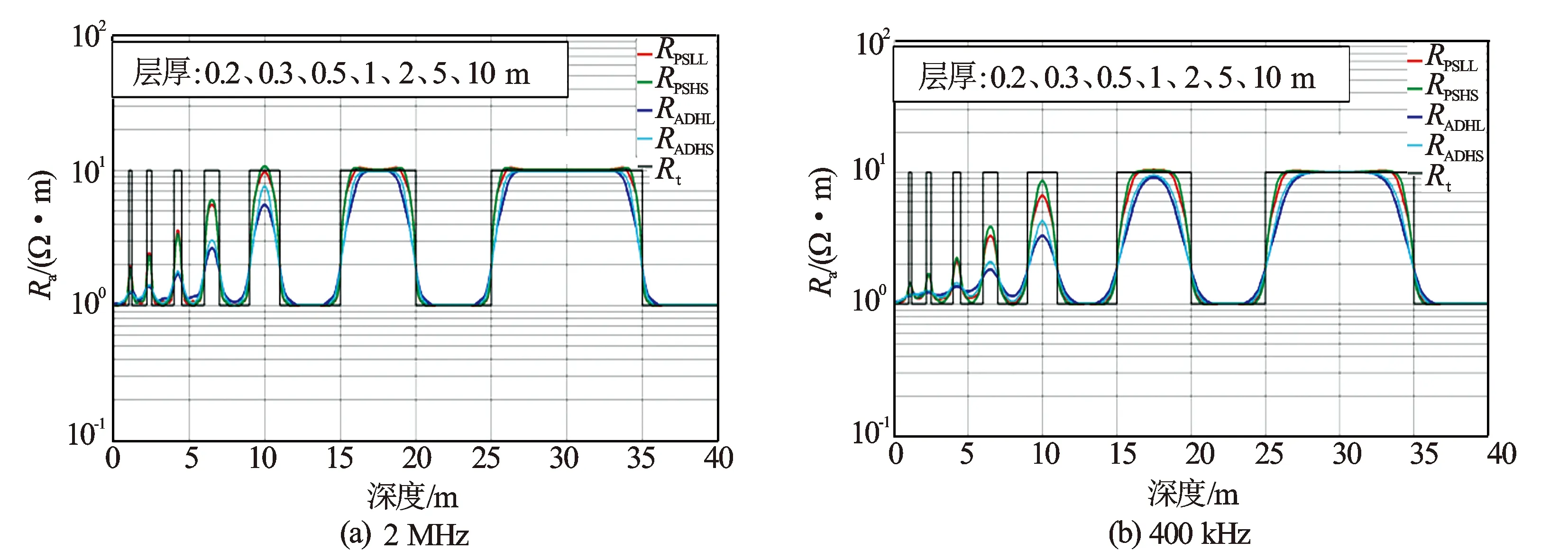
图3 不同频率下层厚对ACPR测井响应的影响图

3.3 井眼环境影响

在井眼直径12 in、泥浆电阻率0.1 Ω·m井眼环境下的测井响应曲线如图4所示。由图4中2 MHz和400 kHz工作频率下各条曲线的井眼影响规律可知,在低电阻率区(电阻率小于10 Ω·m),各条曲线的校正系数基本等于1,表明低电阻率区仪器的测量曲线受井眼环境的影响小,不需要校正;在高电阻率区,仪器的测量响应表现出短源距的校正系数大于1、长源距的校正系数小于1的规律,校正量甚至超过50%,说明井眼环境使得短源距的测量值降低,而使得长源距的测量值升高,表明了井眼环境校正的必要性。

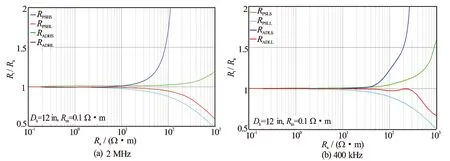
图4 不同频率下井眼对ACPR测井响应的影响图

3.4 倾角及各向异性影响

在水平井和大斜度井测量中,当地层存在各向异性时,此时的测井响应受井轴与地层相对倾角、地层各向异性的综合影响,致使其测量值不能反映真实的地层电阻率,造成解释上的偏差[11]。本文考察了电阻率各向异性——相对倾角解释图版,模型设置:工作频率2 MHz,水平电阻率Rh为1 Ω·m,垂直电阻率Rv为9 Ω·m。由图5仿真结果可知,随着相对倾角的增大,相位差和幅度比视电阻率曲线逐渐偏离水平电阻率;相同相对倾角下,源距越大其视电阻率曲线偏离水平电阻率程度越大;对比相位差和幅度比视电阻率曲线,可知相位差视电阻率偏离水平电阻率程度更大。400 kHz工作频率表现出与2 MHz相同的响应规律,但低频受地层倾角和地层各向异性的影响明显小于高频的影响。

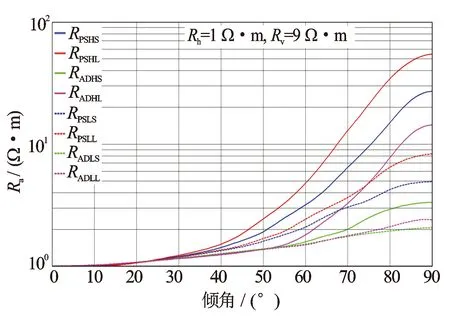
图5 相对倾角及地层各向异性对ACPR测井响应的影响图

4 模型井测试及现场应用

4.1 模型井测试

模拟井直径为4 m,高度9.5 m,井内模型为3层模型,其中第1层层厚为4.410 m,电阻率为2.1 Ω·m;第2层层厚为2.08 m,电阻率为2.65 Ω·m;第3层层厚为3.01 m,电阻率为2.1 Ω·m,以井底作为参考位置分别测量深度位置为1.505、4.05 m和7.295 m处仪器响应。构造与实验测量相同地层模型,用有限元程序进行数值模拟,由表3实验数据与仿真结果的对比,可以看到仿真结果和实验数据吻合得很好,相对误差小于5.0%,说明了ACPR仪器电路设计合理。表3中的数据均为经过空气吊零后的值。

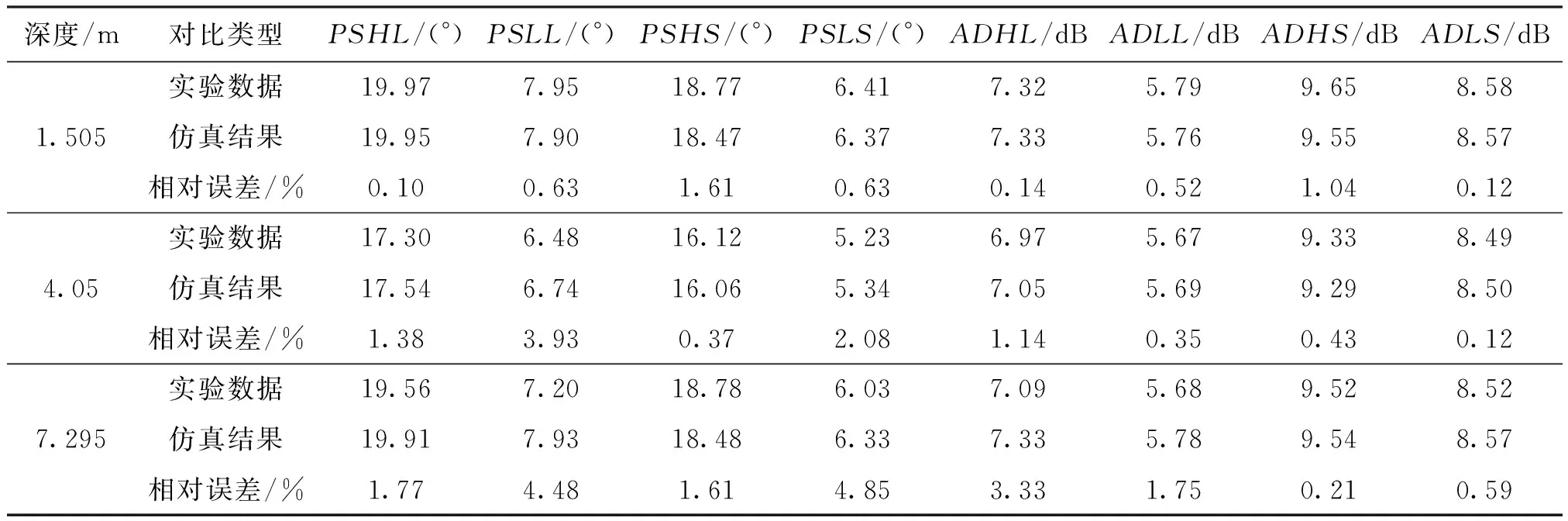
表3 实验数据与仿真结果对比表

4.2 实测井应用

ACPR测井仪已经在海上油田得到了广泛的应用,累计作业几十口井次,作业质量得到市场认可。图6为渤海某口勘探井一段电阻率数据。该井为1口直井,钻头直径12.25 in,井底泥浆电阻率0.12 Ω·m,为保证随钻ACPR电阻率测井仪和电缆双侧向电阻率测井仪测量数据的可对比性,随钻电阻率采用复测数据,2种仪器的测量时间极为接近(见图6)。

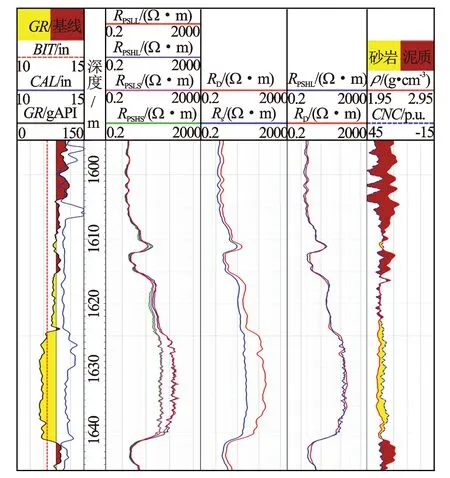
图6 ACPR仪器现场应用结果图

通过图6中第5道的深探测电阻率曲线对比可知,随钻高频长源距相位差电阻率RPSHL和RD深侧向电阻率基本重合,在1 625～1 640 m高电阻率层段,平均电阻率值在140 Ω·m左右,随钻相位差电阻率仍然取得了和双侧向测井一致性较好的电阻率值,说明ACPR仪器在高电阻率段仍然具备较高精度。通过第3道和第4道对比可知,在1 595～1 610 m非渗透层(部分井段扩径严重),双侧向深浅侧向电阻率曲线分离,Rs受井眼影响严重,而ACPR仪器不同探测深度电阻率曲线基本重合,说明ACPR仪器受井眼扩径影响小。综合对比说明了仪器的可靠性和广泛的适用性。

5 结 论

(1) 基于矢量有限元理论,开发了ACPR仪器的正演仿真软件,通过与第三方软件COMSOL仿真结果的对比,验证了所开发程序的正确性。

(2) 考察了ACPR仪器的探测特性,仪器最大探测深度可达到48 in,其中幅度比电阻率的探测深度要比相位差电阻率的深,源距越大探测深度越深,工作频率越低探测深度越深;纵向分层能力上,相位差高于幅度比、短源距高于长源距、高频大于低频。

(3) 考察了各种环境因素对ACPR仪器测量响应的影响,为后续测井资料解释评价奠定了基础。

(4) 通过搭建实验平台构造地层模型,仪器测量数据与软件仿真结果相对误差均小于5.0%,说明ACPR仪器电路设计合理。

(5) 现场测试数据对比表明,ACPR随钻电阻率和双侧向电阻率测量值基本一致,在高电阻率地层中,相位差电阻率仍然可以测量到较高的精度,证明了仪器的可靠性和适用性。

参考文献:

[1] BONNER S, TABANOU J, et al. New 2 MHz Multi-array Borehole-compensated Resistivity Tool Developed for MWD in Slim Holes [C]∥The SPE Annual Technical Conference and Exhibition, Dallas, Texas, USA, October 22-25, SPE 30547, 1995.

[2] ANDERSON B, et al. Modeling 3D Effects on 2 MHz LWD Resistivity Logs [C]∥Transactions of SPWLA 38th Annual Logging Symposium, 1997.

[3] Sperry-Sun, a Halliburton Company. Electromagnetic Wave Resistivity (EWR) Sensor Manual [Z]. 2003.

[4] 高杰, 辛秀艳, 陈文辉, 等. 随钻电磁波阵列补偿传播电阻率测井之电阻率转化方法与研究 [J]. 测井技术, 2008, 32(6): 503-507.

[5] 张中庆, 穆林雪, 张雪, 等. 矢量有限元素法在随钻电阻率测井模拟中的应用 [J]. 中国石油大学学报(自然科学版), 2011, 35(4): 64-71.

[6] 李飞虎, 张中庆, 王卓远. 用矢量棱边元素法模拟三维感应测井响应 [J]. 复旦大学(自然科学版), 2009, 48(5): 560-566.

[7] 仵杰, 段雁超, 李凡, 等. 基于COMSOL仿真软件的阵列感应测井偏心响应计算方法 [J]. 测井技术, 2012, 36(4): 357-360.

[8] 邵才瑞, 张鹏飞, 王正楷. 随钻电磁波测井地层产状因素响应特征三维数值模拟 [J]. 地球物理学进展, 2017, 32(1): 236-242.

[9] 李虎. 复杂介质随钻方位电磁波测井数值模拟与应用基础研究 [D]. 青岛: 中国石油大学, 2013.

[10] 张庚骥. 电法测井(下册) [M]. 北京: 石油工业出版社, 1986.

[11] 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应 [J]. 地球物理学报, 2008, 51(5): 1600-1607.