基于模糊滑模控制的卷纸张力控制系统

祝强, 李立君，高自成

(中南林业科技大学机电工程学院， 长沙410004)

基于模糊滑模控制的卷纸张力控制系统

祝强, 李立君*，高自成

(中南林业科技大学机电工程学院， 长沙410004)

张力控制技术在造纸与印刷设备运行中显得十分重要。针对非线性的张力控制对象，采用一般的滑模变结构控制方法难以避免系统抖振问题，使得目标跟踪精度存在较大误差。通过分析卷纸张力的动态卷绕特性，建立了收卷张力数学模型，并在滑模控制中引入模糊逻辑；采用模糊系统实现模型未知部分的自适应逼近，可有效降低模糊增益，从而消除抖振。以二轴张力控制系统为研究对象进行仿真分析，结果表明系统可以快速准确地跟踪阶跃与正弦信号，并能有效抑制简单滑模控制的抖振问题。为验证该控制系统的可行性，搭建了基于运动控制器的同步伺服试验台，实验结果表明系统在0.25 s以内达到稳定状态，纸卷张力能稳定地进行目标跟随，且只在较小的范围内波动，验证了控制策略的有效性。

纸卷；张力控制；模糊系统；滑模控制；高频抖振；同步伺服试验平台

张力控制系统广泛应用于造纸、印刷、纺织等各类卷绕系统中。在造纸的过程中，张力的大小直接影响到产品的质量，纸张在加工以及纸张的装饰过程中张力控制系统是必不可少的设备[1-3]。在印刷行业中，印刷机上的卷纸外径不断变化，并且这个过程中可能还会出现卷纸不是标准的圆形、重心不与旋转轴重合等情况，这些都将导致纸带上的张力变化。在一些高速胶印设备上，张力波动对印刷精度的影响更加明显，因此张力控制的核心问题是实现纸张的恒张力控制[4]。作为一种典型的非线性系统，张力控制经常存在不可预见的外部或内部干扰，因此也给控制系统的设计提出了较高的要求。

张力控制系统的控制策略在不断地演变，最初采用的是经典控制，比如PID、频域校正等方法，此类方法主要解决单输入单输出问题。在无轴传动的张力控制系统中，由于参数时变、非线性、强耦合等特点无法建立精确的数学模型[5-6]。

滑模变结构控制主要针对较为复杂的非线性系统，这种控制策略的特性是可以迫使系统沿规定的状态轨迹作小幅度、高频率的上下运动[7-8]。这种滑动模态是可以设计且与系统的参数与扰动无关，因此系统具有很好的鲁棒性。但是在实际应用中，滑模控制存在高频抖振现象，这种抖振会使系统超调过大，过渡的时间过长，因此会影响系统动态性能[9]。李琳等[10]将滑模变结构控制方法引入张力控制，验证其所设计的滑模控制系统对于张力控制的有效性，但简单的滑模控制会出现高频抖振，在纸张实际的卷绕过程中效果并不理想。李伟等[11]设计了自调整PID控制系统对纸张卷取过程进行张力控制，主要手段是强化生产线速度变化的跟踪能力，由于纸张会高速卷取且纸卷卷径大范围变化，因此针对PID控制方法进行优化并不能显著改善系统的控制品质和运行稳定性。

笔者将模糊逻辑引入滑模控制，将模糊控制与滑模变结构控制的优点相结合，采用模糊规则，根据滑模到达条件对切换增益进行有效估计，并利用切换增益消除干扰项，从而消除抖振[12]。

1 多轴同步伺服试验平台介绍

张力控制是目前国内许多印刷与造纸等无轴传动设备的基本控制技术。多轴同步伺服试验台基于无轴传动技术，其可搭建出张力模型，并模拟出纸张在卷取时的张力控制过程。通过同步伺服试验台研究在无轴传动伺服控制技术下纸张张力的变化规律，在此基础上进一步设计试验台的控制系统[13]。多轴同步伺服试验平台的硬件主要由工控机、交流伺服电机、运动控制器、张力传感器，以及开卷辊、收卷辊、导向轴，同时配有其他外围的电控和平台结构设备。试验平台也可进行模块化搭建，具有灵活、多样化的特点。

2 张力模型

纸张卷绕过程中收卷端的张力动力学模型如图1所示。根据力矩平衡原理，由图1动力学模型可建立收卷端动态平衡方程：

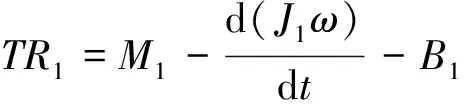
(1)

若在放卷侧，式(1)应该变成如下形式：

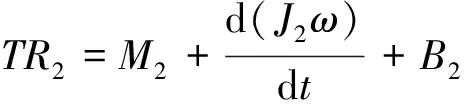
(2)

式中：T为张力；R1、R2分别为收卷侧和放卷侧的纸卷半径，R=D/2；ω为纸卷的转动角速度；M1、M2为伺服电机扭矩；B1、B2为阻尼系数；J1、J2分别为收卷辊和放卷辊的转动惯量。

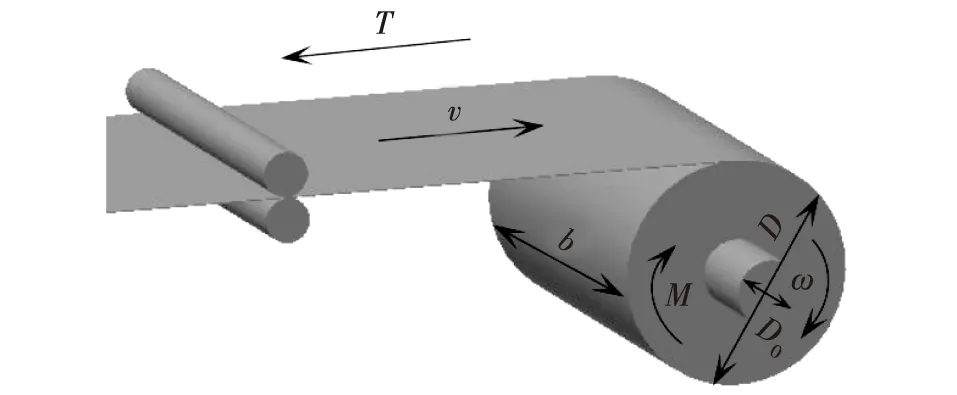
图1 收卷张力动力学模型Fig. 1 The dynamical model diagram of winding tension

由胡克定律可以得到张力的表达式：

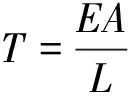
(3)

对上式两边同时求导可以得到下式：

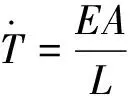
(4)

式中：E为纸张的弹性模量；A为纸张的横截面积；L为纸卷展开的长度；V1和V2分别是收卷端和放卷端纸卷最外侧的线速度。

由此可见，纸卷的进给速度变化时，纸张所受张力会出现波动，并且在绕卷时纸卷半径和转动惯量的变化都将引发张力的波动。纸卷半径的变化是非线性的，且不可避免，因此需要通过对张力的实时监控，改变伺服电机的转速实现抑制和补偿，从而达到控制张力的效果。

由于角速度与线速度之间的关系为ω=V/R，因此式(1)和式(2)可以转化成如下形式：

(5)

(6)

式中：V1、V2分别为收卷端和放卷端纸张的线速度。

由于R1、R2、J1、J2均为时变量，且难以建立数学模型，因此会造成V1、V2的波动，从而影响纸张张力的波动，故由式(4)、式(5)、式(6)构成了系统的一阶微分方程。

上述的张力模型是以收卷端为对象建立的，在实际的卷绕过程中，卷纸张力的波动还会受到纸卷不圆度以及收卷辊、放卷辊弯度的影响。

3 模糊滑模控制器的设计

3.1 张力控制原理

在纸张的卷绕过程中，相邻两辊之间存在的速度差导致纸张产生内应力，这种内应力如不加以控制，可能会出现纸张断裂的情况，在工业现场这种情况是不允许的[14-15]。张力控制实质上是控制相邻两辊之间的速度差，纸张的线速度是通过速度编码器获取，实时的张力是由张力传感器获得。通过张力动力学模型分析可知张力的变化情况，针对不同类型纸张，设定不同的张力值。利用模糊滑模控制器快速调节伺服电机的速度，使张力值在设定的预期值附近小幅度变化，从而实现纸张卷起的同步控制，即恒张力控制。

3.2 滑模控制

依据滑模控制器设计的流程，除了要设计滑模面外，还要设计滑模控制律[16]。滑模控制器可将张力稳定在可控的波动范围内。

定义滑模系统的跟踪误差：

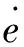
(7)

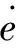
定义滑模函数为：

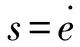
(8)

定义趋近律为：

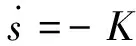
(9)

通过式(4)、(7)、(8)、(9)可以解出控制律为：

(10)

滑模控制设计完成之后对其进行稳定性分析，此时在系统中加入干扰量E(t)，同时取下列关系：

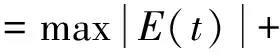
(11)

取Lyapunov函数为

(12)

则可以得到下式：

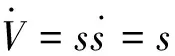
(13)

将趋近律代入式(12)可得：

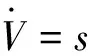
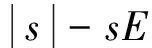
(14)

在控制律中切换增益K(t)是造成抖振的原因。由于干扰E(t)是不确定且随时间变化的，而K(t)是用于补偿不确定项E(t)的，以保证滑模存在性条件得到满足。为了降低抖振，K(t)应随着E(t)的变化而变化。

3.3 模糊滑模控制器设计

由于模糊系统可以对任意的连续与非连续函数进行精确逼近，将其引入到滑模控制系统当中可以有效抑制系统中的抖动问题[17]。

可建立如下模糊规则：

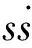
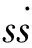
模糊系统输入和输出的隶属度函数如图2、图3所示。

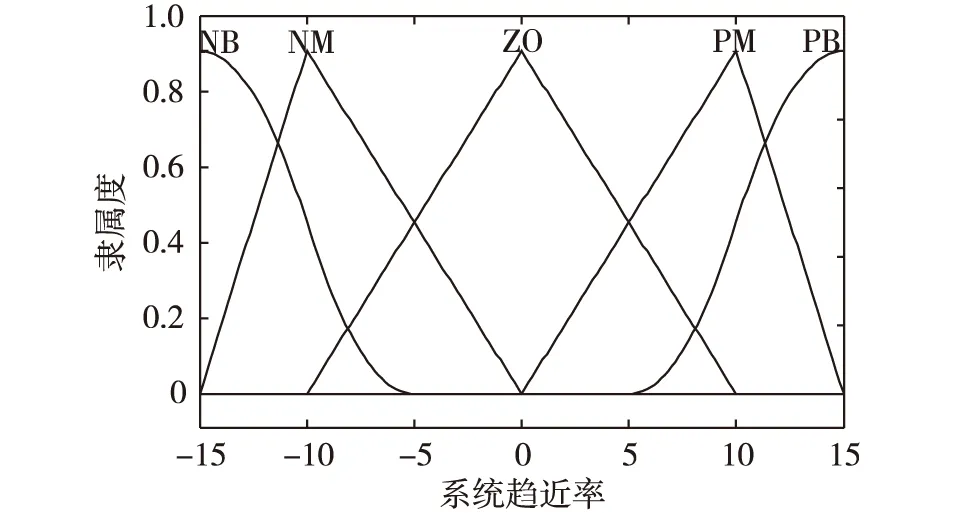
图2 模糊输入隶属度函数Fig. 2 The membership function of fuzzy input

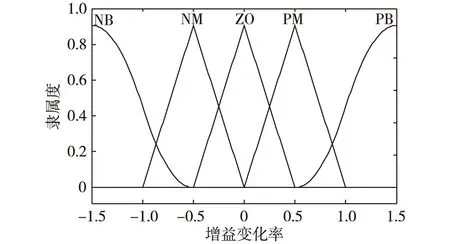
图3 模糊输出隶属度函数Fig. 3 The membership function of fuzzy output

模糊规则如下：

同时采用积分法进行上界估计[18]：

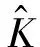
(14)

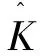
(15)

模糊滑模控制系统的结构如图4所示。通过引入模糊逻辑与滑模控制进行结合，从而实现模型未知部分的自适应逼近，可有效降低模糊增益。

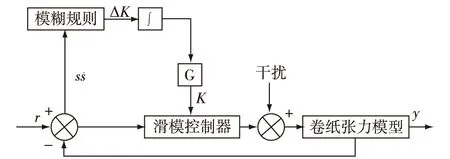
图4 模糊滑膜控制系统结构Fig. 4 The structure of fuzzy sliding mode control system

4 模糊滑模控制系统仿真分析

为验证上述控制方法，利用Matlab软件对其进行系统仿真。设置仿真参数为G=400，c=150。根据控制律式(15)，分别取阶跃信号和正弦信号为目标信号，采用基于模糊切换增益调节的滑模控制器进行仿真，得到的仿真结果如图5、图6所示。

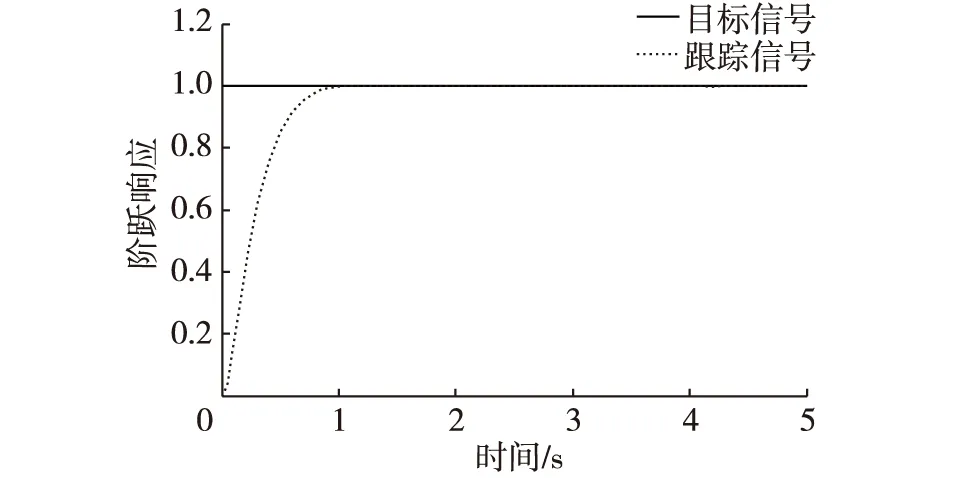
图5 阶跃输入张力响应图Fig. 5 The response curve of step input

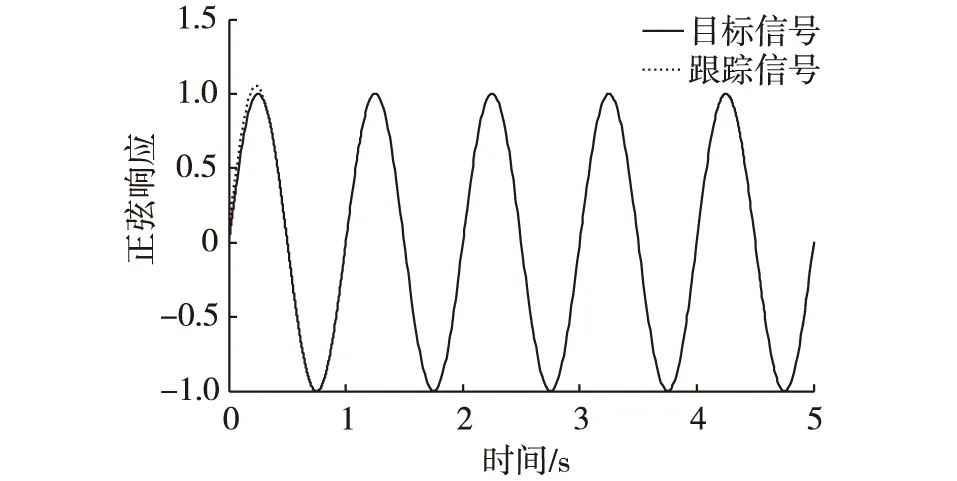
图6 正弦信号输入张力响应图Fig. 6 The response curve of sinusoidal input

阶跃信号输入时张力响应迅速且无超调量，能够满足快速响应和高精度要求；同时，为了得到系统的跟踪特性，采用频率为1、幅值为1的正弦波信号作为目标信号得到响应曲线。结果表明，跟踪信号在经过初期调整后也能很好地跟随目标值。

5 试验验证与分析

上述控制系统设计是基于模糊增益调节的滑模控制，为了验证该系统的可行性，搭建了针对纸卷张力控制的同步伺服试验台(图7)。试验台的控制系统采用了Rexroth公司NYCe4000型运动控制器，该型控制器能在PC端完成程序的编写并下载至控制器执行。试验台的动力元件采用三洋伺服电机，张力传感器采用三菱LX-030TD型。

图7 张力控制试验台Fig. 7 Experimental platform of tension control

由试验结果(图8、图9)可知：在模糊滑模控制器的调节下，系统在0.25 s以内即达到稳定状态，伺服电机的速度跟踪误差逐渐收敛，速度曲线平滑，没有出现大幅抖动；速度在达到稳定值附近时，速度的抖振得到了有效抑制，抖振幅值在±0.5 mm/s以内。在进行张力跟踪试验时，将张力目标值设定为4 N，试验结果显示在试验开始阶段，张力的瞬间值较大，主要是电机的初期加速过程所致。在达到稳定状态后，张力值能够稳定地在4 N附近进行跟随，系统反馈的张力值的抖振得到有效抑制。因此将模糊逻辑引入滑模控制能够有效抑制简单线性滑模控制存在的抖振问题，可满足纸卷卷绕过程对张力控制的要求。

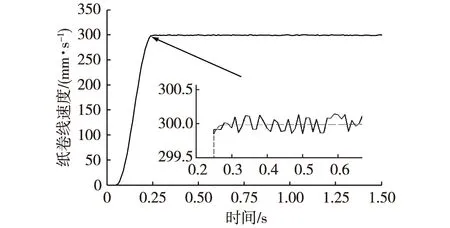
图8 伺服电机速度试验跟踪结果Fig. 8 The tracking results of servo motor speed test

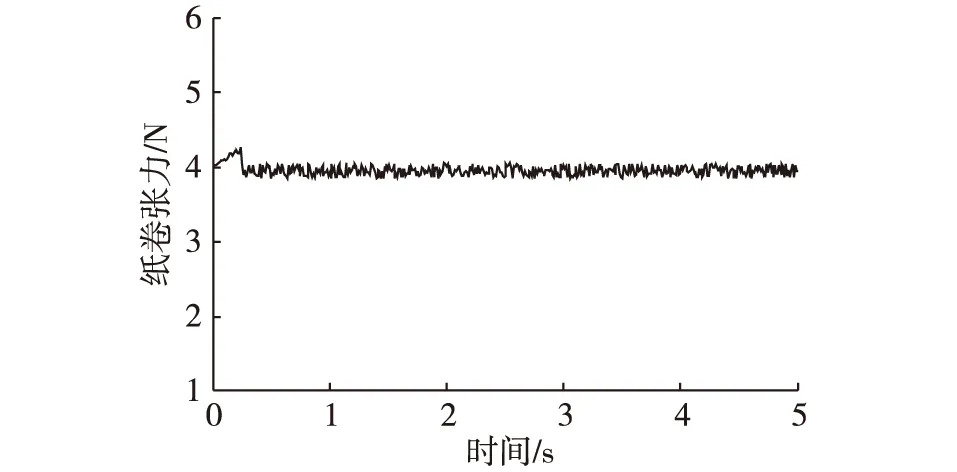
图9 张力试验跟踪结果Fig. 9 The tracking results of tension test

6 结 语

笔者针对纸张张力控制系统建立了张力动力学模型，在此基础上提出了一种基于模糊滑模变结构控制的方法，对纸张卷绕过程的张力进行控制。仿真结果表明所设计的模糊滑模控制器具有跟踪精度高和响应速度快的特点，综合了滑模控制和传统模糊控制的优点。为验证算法的可行性，搭建了基于运动控制器的试验平台，实验结果表明系统在0.25 s以内就能达到稳定状态，控制系统能够将张力稳定在目标值附近进行跟随，张力波动范围小，系统控制精度较高，满足纸卷卷绕过程对张力控制的要求。

[1]张义兵, 戴瑜兴, 袁巨龙, 等. 多线切割机线张力控制系统设计实现[J]. 机械工程学报, 2009, 45(5):295-300. ZHANG Y B, DAI Y X, YUAN J L, et al. Design and impl-ement of wire tension control system for multi-wire saw[J]. Journal of Mechanical Engineering, 2009, 45(5):295-300.

[2]张池, 杨琳. 基于PLC与变频器的造纸机张力控制系统[J]. 中国造纸, 2010, 29(9):53-55. ZHANG C. YANG L. Realization of tension control of paper machine based on PLC and VFD[J]. China Pulp & Paper, 2010, 29(9):53-55.

[3]郭献军. 卷筒纸印刷中张力与套准关系的研究[J]. 包装工程, 2014, 36(7):133-138. GUO X J. The relationship between tension and register in web printing[J]. Packaging Engineering, 2014, 36(7):133-138.

[4]王凯, 马春敏, 康存锋, 等. 无轴印刷张力控制系统的研究[J]. 机械设计与制造，2010(4):106-108. WANG K, MA C M, KANG C F, et al. Research on shaftless printing tension control system[J]. Machinery Design & Manufacture, 2010(4):106-108.

[5]王春香, 王永章, 路华, 等. 精密张力控制系统及其控制精度的研究[J]. 仪器仪表学报, 2000, 21(4):407-408. WANG C X, WANG Y Z, LU H, et al. A research of the precise tension control system and control precision[J]. Chinese Journal of Scientific Instrument, 2000, 21(4):407-408.

[6]张鹏, 杨瑞峰, 张学良, 等. 速度差间接张力控制系统的建模与研究[J]. 中北大学学报(自然科学版), 2013, 34(6):678-681. ZHANG P, YANG R F, ZHANG X L, et al. Research on modeling for the indirect tension control system based on difference of rotational speed[J]. Journal of North University of China(Natural Science Edition), 2013, 34(6):678-681.

[7]杨梅. 滑模变结构在收卷张力控制系统中的应用与仿真[J]. 包装工程, 2013, 34(3):44-48. YANG M. Application and simulation of sliding mode control in winding tension control system[J]. Packaging Engineering, 2013, 34(3):44-48.

[8]刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3):407-418. LIU J K, SUN F C. Research and development on theory and algorithms of sliding mode control[J]. Control Theory & Applications, 2007, 24(3):407-418.

[9]LIU J K, WANG X H. Advanced sliding mode control for mechanical systems:design, analysis and matlab simulation[M]. Beijing:Tsinghua University Press, 2011.

[10]李琳, 林炯辉, 邹焱飚. 基于滑模变结构的张力控制系统设计[J]. 机械设计与制造, 2016(4):175-177. LI L, LIN J H, ZOU Y B. Design of tension control system based on sliding mode control[J]. Machinery Design & Manufacture, 2016(4):175-177.

[11]李伟, 王友权, 董继先, 等. 自调整PID控制在卷取张力中的设计与仿真[J]. 包装工程, 2014, 35(11):67-70. LI W, WANG Y Q, DONG J X, et al. Design and simulation of self-adaptive PID control system in tension control[J]. Packaging Engineering, 2014, 35(11):67-70.

[12]KIM S W, LEE J J. Design of a fuzzy controller with fuzzy sliding surface[J]. Fuzzy Sets and Systems, 1995, 71(3):359-367.

[13]陈康昊, 郑刚, 杨建武, 等. 无轴传动控制实验平台的开发研究[J]. 现代制造工程, 2010(12):141-144. CHEN K H, ZHENG G, YANG J W, et al. Research and development of shaftless driving experiment technology[J]. Modern Manufacturing Engineering, 2010(12):141-144.

[14]李明辉, 柴德喜. 卷纸机间接张力控制的原理及实现[J]. 电机与控制应用, 2011, 38(4):47-49. LI M H, CHAI D X. Principle and application of indirect tension control for pope reel driving[J]. Electric Machines & Control Application, 2011, 38(4):47-49.

[15]盛卫锋, 周一届, 姜旻. 印刷机械中的张力控制[J]. 包装工程, 2001, 22(2):4-7. SHENG W F, ZHOU Y J, JIANG M. Controlling tension on printing machines[J]. Packaging Engineering, 2001, 22(2):4-7.

[16]刘金琨. 滑模变结构控制MATLAB仿真基本理论与设计方法[M]. 北京：清华大学出版社，2015.

[17]周之光，张桂香. 基于带切换增益模糊调节的滑模控制算法的车辆电液制动系统[J]. 汽车工程, 2010, 32(3):228-233. ZHOU Z G, ZHANG G X. Vehicle EHB system based on sliding mode control algorithm with switch gain fuzzy modulation[J]. Automotive Engineering, 2010, 32(3):228-233.

[18]曹艳, 李小兵, 吴博文. 基于模糊增益调节的机器人滑模自适应控制[J]. 计算机仿真, 2015, 32(11):368-372. CAO Y, LI X B, WU B W. Sliding mode adaptive control of robot based on fuzzy gain adjustment[J]. Computer Simulation, 2015, 32(11):368-372.

Study of the paper tension control system basedon the fuzzy sliding mode control

ZHU Qiang，LI Lijun*，GAO Zicheng

(Mechanical and Electrical Engineering College，Central South University of Forestry and Technology，Changsha 410004, China)

Tension control technology is very important in the operation of papermaking and printing equipment. In view of the nonlinear tension control system with sliding mode, variable structure control is difficult to avoid chattering problem that could result in big error of tracking precision. The characteristics of this control strategy are to force system vibration with low amplitude and high frequency along the specified state trajectory. The sliding mode can be designed and the parameters of the system are independent of the disturbance. But in practical application, the sliding mode control has the phenomenon of high frequency chattering and long transition time. Tension mathematical model is established by analyzing the dynamic characteristics of tension. The fuzzy logic is introduced to achieve the adaptive approximation of the unknown part of the model in order to eliminate the chattering and reduce the fuzzy gain effectively. The biaxial tension control system is selected as the research object in the simulation analysis. The results show that the system can rapidly and accurately track the step and sinusoidal signal, and can effectively restrain the chattering of sliding mode control problem. To validating the feasibility of the system, an experimental platform of tension control based on motion controller was built. The experimental results show that the system reaches steady state within 2.5 s, and the tension of scroll can track stably and fluctuate within small rang. The effectiveness of the control strategy which can provide reference for the actual tension control method can be verified.

paper reel；tension control；fuzzy system；sliding mode control；high frequency chattering；synchronous servo test platform

2016-08-21

2016-12-07

湖南省高校科技创新团队项目(2014207)。

祝强，男，研究方向为现代机械设计及理论。通信作者：李立君，女，教授。E-mail:junlili1122@163.com

TP273

A

2096-1359(2017)02-0122-05