“沪港通”对沪深股市收益率的影响研究
——基于VAR-EGARCH模型实证分析
2017-04-24许勇
许 勇
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
“沪港通”对沪深股市收益率的影响研究
——基于VAR-EGARCH模型实证分析
许 勇
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
以2010年1月至2016年4月沪深港股市日收益率及日成交额为样本,基于VAR-EGARCH模型分析“沪港通”改革前后沪深股市收益率受到的影响。根据VAR及方差分解结果表明,“沪港通”后对香港市场、上海市场收益率影响相比“沪港通”前有较大提高,但这种影响仍然非常较小;相反,“沪港通”前后深圳股市收益率受到香港的影响比较大。根据EGARCH分析结果,沪深股市波动越大收益率越小,同时受等强度的新息冲击会引起两者的非对称反应。
“沪港通”;“深港通”;收益率;VAR-EGARCH
股市通常被认为是国家宏观经济的晴雨表,我国的资本市场的开放程度不如欧美等发达国家,两者相互影响程度也不如欧美等发达国家。但就沪深股市来说,两者的市场收益率相关性、波动性等方面密切相关。国外学者关于股市收益率研究方面,Eun、Shim(1988)通过对美国股市和其他国家的股票市场研究发现,[1]美国股票市场波动会很快影响到其他国家股票市场,相反其他国家股票市场的波动对美国股票市场的影响较小。French(1987)运用GARCH模型检验美国股市预期收益率与波动性的相关关系,发现股市预期收益率与波动成正相关,未来预期收益率与未来预期波动成负相关。[2]Glosten(1993)以月度收益率为单位对美国股市的股价指数采用非对称EGARCH模型进行实证分析,[3]结果表明收益率负残差引起方差的增长,而收益率正残差导致方差的减少。Engle(1995)对美国股市单个股票收益序列进行研究,证明单只股票收益序列存在显著的ARCH效应。[4]Chuang(2007)利用BEKK-MVGARCH模型对东亚六国的股市收益率的溢出效应和波动性进行研究。[5]
近年来,国内学者对此也进行了大量研究。王安兴、孙琼等(1998)运用GARCH(1,1)模型对深证市场的收益率进行研究,结果显示:收盘价格的收益序列之间存在序列相关,而对于单只股票来说市场尚未达到弱势有效的程度。[6]张兵、李晓明(2003)采用GARCH模型、方差比检验和Box-Pierce Q检验分析了上证股市收益率,证明我国股市有渐进效应。[7]李红权、马超群(2005)应用修正的R/S分析及ARFIMA模型证实我国股市具有显性的非线性特征,收益率的自相关性较弱,并且收益率的波动性方面表现出显著的长期记忆效益。[8]王耀(2007)在研究上证指数收益率的波动性时发现,沪市指数收益率服从高阶ARCH过程。[9]胡坚等(2008)对2002-2008年上海股市与香港股市的联动分析得出,沪市与香港股票市场之间是相互独立的,彼此之间并未受到共同影响。[10]蔡晓春等(2009)利用二阶非对称效应的TARCH模型对深证综指收益率研究发现:滞后期1、4阶对深证综指收益率变化影响较强。[11]石建勋等(2010)选取S&P 500指数、恒生指数、恒生国企指数及恒生AH股溢价指数逐一与沪深300指数分析,探讨两地股市联动原因,结果也证明造成两地股市的主要原因是股市本身。[12]何诚颖等(2013)基于SV-TVP-SVAR模型对汇率与股票价格之间的动态关系展开研究,[13]结果表明汇率与股票价格之间具有明显的时变性,汇率与股价波动在不同的时点上具有较大的不对称性。刘文文、乔高秀(2014)对期货与现货市场关系研究表明,两者互为Granger因果关系,期货价格发现功能领先于现货市场,同时从期货市场到现货市场存在显著的波动溢出。[14]谢赤、龚雯辉(2016)运用CBP-GARCH模型对期货市场与现货市场收益率的跳跃现象研究,表明期现货收益率存在共同跳跃现象,这种跳跃的频率受到两个市场收益率波动的影响。[15]相对于国外比较发达的资本市场,我国的资本市场开放仍然还有很长的路要走。
1 数据来源与理论模型
1.1 数据来源
以股票指数为对象研究中国股市的波动性及相关性,股票的价格指数表示上市公司股票经过加权平均以后的价格水平及其变动的指标。选取2010年1月至2016年4月上证综合指数(SHI)与深证成份指数(SZI)的收盘价作为波动性与收益率研究对象,剔除非交易日共得到3919个样本数据,所有数据均来自wind数据库。
1.2 脉冲响应函数与方差分析
脉冲响应函数是用来衡量来自随机扰动项的一个标准差大小的冲击对内生变量当期值和未来值的影响,考虑二阶VAR(2)模型:
xt=α11xt-1+α12xt-2+α13yt-1+α14yt-2+μ1t
(1)
yt=α21xt-1+α22xt-2+α23yt-1+α24yt-2+μ2t
(2)
模型中随机误差项称为“新息”,μ1,μ2为白噪声序列,且两者不相关。
方差分析是通过分析内生变量的冲击对内生变量的变化的贡献度,其基本思想为:
设多变量的VAR(P)模型为:
Yt=A1Yt-1+A2Yt-2+…+ApYt-p+Ut
(3)
其中,Yt是k维内生变量向量,A0,A1,A2…,Ap是参数矩阵,p是滞后期。Ut是随机误差项。
Yt的第i个变量可以写成:

(4)
则其方差为:
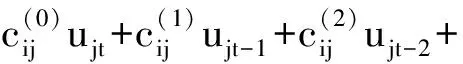
(5)
此处还假定随机项向量的协方差矩阵是对角矩阵,则yi的方差是上述方差的k项简单和:

(6)
便可得到贡献率:
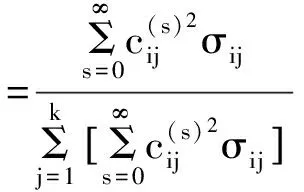
(7)
1.3 ARCH检验与EGARCH模型
残差序列是否存在ARCH效应,最常用的检验方法是拉格朗日乘数法,即ARCH—LM检验。具体步骤如下:

(3)假设检验H0∶α1=α2=…=αp=0 H1∶∃αi≠0(1≤i≤p)
检验统计量为:
LM=nR2χ2(p)
(8)
Nelson(1998)提出一种非对称GARCH模型,即EGARCH模型。基本EGARCH模型如下:
Rt=c+ασt+ut
(9)

(10)


2 沪深港股市实证分析
2.1 沪、深股市波动性与收益率统计特征
如果没有特别说明,我们均研究对数收益序列的百分数,其定义为:
rt=ln(pt)-ln(pt-1)其中,pt为本期的收盘价格,pt-1为一期的收盘价格。上证综合指数收益率(SHR),深证成份指数收益率(SZR),香港恒生指数收益率(HSR)。
表1 SHR、SZR序列基本统计特征
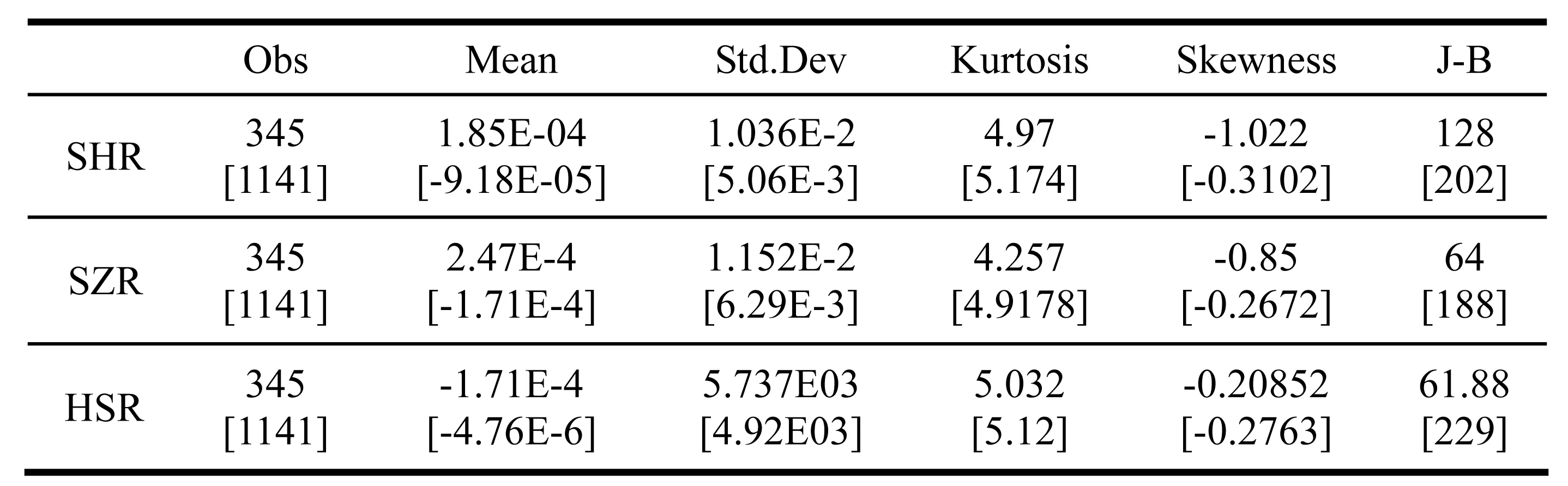
注:[]是“沪港通”之前的统计量
表2 SHR、SZR、HSR时间序列ADF检验
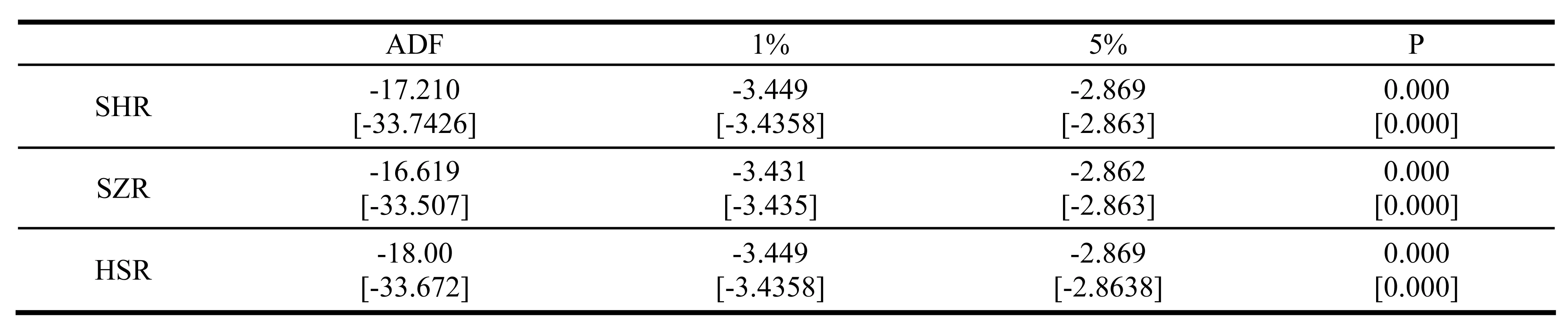
从表2中收益率的检验可知,“沪港通”前后SHR、SZR、HSR均通过ADF检验具有平稳性,检验沪深股市每日成交额之间同样具有平稳性。
2.2 沪、深股市脉冲响应分析
SHR在“沪港通”前后受到SZR、HSR的VAR脉冲响应结果如表3所示。
表3 HSR、SZR对SHR冲击响应

注:[]是“沪港通”之前的冲击

图1 “沪港通”前后HSR、SZR对SHR冲击响应
根据图1“沪港通”前后的脉冲响应(横轴表示冲击作用滞后期天数,SHR1、SZR1、HSR1表示“沪港通”之后收益率,SHR2、SZR2、HSR2表示“沪港通”之前收益率)可知,“沪港通”之前,在本期给HSR一个正向标准差新息冲击后,SHR1在第1期正向反应达到最大值为2.744E-3,以后各期中给HSR 1个正向标准差新息冲击后对SHR均具有反向冲击效应,并且这种效应仅持续到第3期。
表4 SHR、HSR对SZR的冲击响应

注:[]是“沪港通”之前的冲击影响

图2 “沪港通”前后SHR、HSR对SZR的冲击响应
根据图2 “沪港通”之前,给SHR一个正标准差新息冲击后,SZR在第1期没有反应,在第2期SHR的正标准差新息对SZR冲击具有非常小的正向冲击效应,第3期HSR对SZR的冲击效应为负直至减小到零。 “沪港通”之后,SHR对SZR的冲击效应持续时间仍然大于“沪港通”之前的时间。香港市场对深圳市场的影响方面,由图2可以看出,“沪港通”之前给HSR一个正标准差新息冲击对SZR以后各期的冲击效应均为负;“沪港通”实施之后给HSR一个正标准差新息冲击,SZR在第1期仍然得到一个负向冲击效应,而这种冲击响应要小于“沪港通”之前的影响,第2期HSR对SZR的正向冲击效应最大,然后依次减小最后衰减到0。
2.3 沪、深股市收益率EGARCH模型估计
根据上述脉冲响应分析,加入沪深港股市每日成交额进一步分析SHR、SZR的影响结果,建立沪、深两个市场的收益率与股市每日成交额不同的多元回归模型。具体模型如下:
shrt=αshrct+βshrt-1+rhsrt+εt1
(13)
szrt=αszrct+βszrct-1+rhsrt+εt2
(14)
表5 SHR、SZR回归参数

注:***、**、*分别为1%、5%、10%显著性水平,下同
根据“沪港通”实施以来SHR、SZR多元回归模型的残差ARCH-LM检验(见表6)可以得出,SHR、SZR的回归方程的残差不存在ARCH项。由表5的回归结果可知,参数显著性较高通过检验,SHR和SZR自身的本期收益率与本期的成交额呈正相关性,SHRC每增加1个单位的百万交易额,对SHR提高0.001298个单位;上一期SHR增加或降低1个单位收益率,对本期SHR增加或减少0.057803个单位。本期HSR对本期SHR的影响是SHRC及上一期SHR中影响因素最大的为0.701027,说明“沪港通”以来香港市场HSR与上海市场的联动性加强。
表6 SHR、SZR残差ARCH-LM检验

通过以上对“沪港通”以来SHR修正后的EARCH(1,1)模型可知,均值方程(见表7)参数SQR(GARCH)项系数为-0.258063,说明上海市场股市波动增加1%,收益率将减少-0.258063%。同理,深圳市场波动增加1%,收益率将减少-0.327973%。
表7 SHR、SZR均值方程参数

3 结论
通过构建VAR-EGARCH模型,分析“沪港通”前后香港市场与大陆市场股市收益率及其影响因素,得出以下结论:
3.1“沪港通”实施以来,香港股市与深圳股市对上海市场的影响有所增加,但影响上证指数收益率的主要因素仍然是本身的新息。HSR对SHR的新息影响虽然相对“沪港通”之前增大但是这种影响仍然较弱。
3.2上证指数收益率对正向冲击反应小于深证成份指数收益率对正冲击反应,深证成份指数收益率对负的冲击反应大于上证指数收益率对负的冲击反应。这一方面反映出高收益往往伴随高风险的特点,另一方面也反映出沪深股市上涨慢、下跌快,“熊市”多于“牛市”的基本特征。
3.3“沪港通”实施以来,香港市场对上海市场的影响,如果仅从前后影响比值来说,“沪港通”对上海市场的影响有较大的提高;如果考虑影响程度,香港市场对上海市场的影响远小于香港市场对深圳市场的影响。
[1]Eun,R.F.,&S.Shim.International Transmission of Stock Market Movement[J].Jouarnal of Financial and Quantitative Analysis, 1989 (2):241-244.
[2]French K,Schwert G W.Expected stock return and volatility[J].Journal of Financial Economics,1987,19:3-28.
[3]Glosten L R, Jagannathan R, Runkle D. On the Relation between the Expected Value and the Volatility of the Normal excess Return on stocks [J].Journal of Finance,1993(4):1779-1801.
[4]Engle,R.F.&F.K.Kroner.Multivariate simultaneous generalized ARCH[J].Econometric Theory,1995,11:122-150.
[5]Chuang I Y,Lu J R,Tswei K.Interdependence of international equity variances:Evidence from East Asian markets[J].Emerging Markets Review,2007,8(4):311-327.
[6]王安兴,孙琼,林少宫.中国外汇市场波动分析[J].统计研究,1998,15(1):25-29.
[7]张兵,李晓明.中国股票市场的渐进有效性研究[J].经济研究,2003(01):51-61.
[8]李红权,马超群.收益率与波动性长期记忆效应的实证研究[J].财经研究,2005(8):29-35.
[9]王耀.GARCH模型在计算上海股市风险价值中的应用研究[J].经济问题探索,2007(8):153-157.
[10]胡坚,吕鹏博.上海股市与香港股市联动分析[J].山西财经大学学报,2008(12):93-97.
[11]蔡晓春,叶发强.基于TARCH模型深证综指收益率的实证分析[J].统计决策,2009.
[12]石建勋,周浩.内地股市与香港股市联动原因的实证分析[J].国际经贸探索,2010(11):55-61.
[13]何诚颖,张龙斌,陈薇.基于高频数据的沪深300指数期货价格发现能力研究[J].数量经济技术经济研究,2011(5):139-151.
[14]刘文文,乔高秀.我国股指期货市场价格发现功能和波动溢出效应研究-基于VECM-DCC-MVGARCH模型[J].武汉金融,2014(8).
[15]谢赤,龚雯辉.基于CBP-GARCH模型的股指期现货收益率共同跳跃研究[J].武汉金融,2016(3).
Class No.:F832.5 Document Mark:A
(责任编辑:宋瑞斌)
Impact of Shanghai-Hong Kong Stock Connect on Stock Market Returns of Shanghai and Shenzhen Based on the VAR-EGARCH Model Analysis
Xu Yong
(School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, Anhui 233030,China)
From January 2010 to April 2016 in Shanghai and Shenzhen stock market return and turnover as samples to analyse the influence of the "return of Shanghai and Shenzhen stock market by rate before and after Shanghai and Hong Kong through reform based on VAR-EGARCH model. According to VAR and variance decomposition results, after Shanghai and Hong Kong through the Hongkong market, Shanghai market yield effect "has greatly improved compared to Shanghai and Hong Kong before, but this effect is still very small; on the contrary, the Shenzhen stock market returns in Hongkong affected by the larger rate before and after Shanghai and Hongkong. According to the results of EGARCH analysis, the greater the volatility of the Shanghai and Shenzhen stock market, the smaller the yield, while the impact of equal intensity will cause the asymmetric reaction.
Shanghai-HongKong Stock Connect; Shenzhen-HongKong Stock Connect; rate of return; VAR-EGARCH
许勇,硕士,安徽财经大学统计与应用数学学院。研究方向:宏观经济分析。
1672-6758(2017)04-0109-6
F832.5
A
