最小二乘法曲线拟合的RTC补偿在智能电表中的应用
2017-04-24王岳平张道振邱于保
王岳平,张道振,邱于保
(1.华立科技股份有限公司,浙江 杭州 310023;2.万向一二三股份有限公司,浙江 杭州 311215)
最小二乘法曲线拟合的RTC补偿在智能电表中的应用
王岳平1,张道振2,邱于保1
(1.华立科技股份有限公司,浙江 杭州 310023;2.万向一二三股份有限公司,浙江 杭州 311215)
在降本增效要求的推动下,智能电表的电机控制单元(MCU)逐渐采用片上系统(SoC)方案,在集成电子技术发展基础上趋向多元件集成。针对目前应用的大多数SoC芯片内置实时时钟(RTC)模块需要时钟补偿才能满足国网±0.5 s/d精度要求的问题,提出了通过硬件温度检测和在软件上采用最小二乘法曲线拟合晶体振荡器温度特性对RTC进行温度补偿的方案,结合Matlab最小二乘法曲线拟合工具进行数据分析与研究,并采用三次曲线拟合补偿曲线,经测试验证可达到在-45~+75 ℃的温度范围内±0.5 s/d的系统精度要求。该方法已通过批量验证,完全能满足国家电网新一代智能电表的时钟精度要求,为智能电表等自动化仪表的RTC方案选择提供了新思路和新方向。
能源; 电力; 智能电表; 最小二乘法; 温度补偿; Matlab; 精度
0 引言
智能电表分费率及预付费要求时钟精度在±0.5 s/d以内,且在电池供电时须保证时钟正常工作。考虑到电池的使用寿命,一般选择低频、低功耗的32 768 Hz石英晶体振荡器作为实时时钟(real time clock,RTC)的时钟源。
晶体振荡器由晶体单元和各种半导体组成,频率特性主要取决于其内部晶体单元,而晶体单元特性取决于切割工艺,切割工艺决定了晶体振动模式、频率范围和温度特性[1-4]。晶体振荡器根据切割工艺主要有音叉型、AT切型、声表面波型三种,每种都具备特有的频率范围和温度特性。智能电表的RTC振荡器常选择音叉型,其温度特性曲线表现为抛物线,在全温度范围内很难满足仪器仪表的精度要求。另外,晶体的生产厂家、生产批次和工艺的差异等也会对其温度特性曲线和晶体固定频率产生影响,所以必须对晶体振荡器进行温度和固定频偏校正。
1 校正方案对比
在智能电表设计中,RTC一般有以下三种方案。
①采用时钟芯片。该芯片自带补偿,时钟输出精度稳定、可靠,操作与应用方便;但其不仅价格高、有悖于降本增效,而且电机控制单元(moter control unit,MCU)必须通过I2C总线获取日历时间等相关信息,在电池供电环境下频繁读取,会增加额外功耗,减少电池使用寿命。
②采用片上系统(system on a chip,SoC)+预设拟合曲线。RTC以独立模块的方式强制集成在MCU芯片上,片内预设供应商提供的温度补偿拟合曲线和温度补偿机制,用户只需频偏校正,操作方便。但由于该方案需要定制对应的晶体振荡器,且更换晶体振荡器须通过供应商修改预置拟合曲线,故延长了供货周期。
③采用SoC,RTC模块同方案二集成在MCU芯片上。因片内既无温度补偿机制,也无预设的温度补偿拟合曲线,所以应用时必须进行温度补偿和频偏校正才能满足时钟精度要求。
应用厂家常因温度补偿不到位导致RTC精度不达标而选用方案一。
表1对比了这三种RTC方案的优缺点。

表1 RTC方案优缺点对比
针对方案三,提出以最小二乘法曲线拟合的方式拟合温度补偿曲线,对晶体振荡器因温度影响而产生的频率偏差进行补偿,以达到时钟输出稳定、高精度的要求,从而在降本增效的基础上,为智能电表等仪表生产厂家选择自由定制的RTC方案提供帮助。
2 RTC校正原理
RTC的校正方式可分为模拟补偿和数字补偿两种[4-5]。
模拟补偿即硬件自校正,其通过提高或调整晶体振荡器晶体本身、负载电容、电压、应力及优化硬件拓扑结构[1-6],以达到理想的精度。
数字补偿通过补偿寄存器(trim-register)在固定时间间隔内增减时钟个数进行调整,从而达到补偿目的[6-8];通常有调整高频振荡时钟个数和低频32 768 Hz时钟个数两种方法。
晶体振荡器补偿原理如图1所示。

图1 晶体振荡器补偿原理图
通过修改预分频器和调整补偿寄存器的数值,可增减计数周期内低频32 768 Hz晶体振荡器的时钟个数,从而影响计数器半秒或秒的进位频率,比如STM32F1XX系列、STM32L1XX系列采用此方法;SH79F642采用调整计数周期内高频振荡时钟个数的方法。
相对高频计数,低频计数会在固定周期内增减不固定的低频时钟个数[7-8],导致因秒输出不均匀而跳出一个大误差值[4,7]。其虽不影响累积误差,但如需秒输出均匀,则可采用类似文献[7]的方法。该方法在固定时间周期内,使用定时器(高频计数)捕捉方式测量并计算周期内的累计计时误差;然后平均到每秒,根据每秒误差,修改半秒或秒窗口定时器,比较寄存器数值,通过定时中断方式输出半秒或秒信号。无论是低频计数还是高频计数,其补偿原理都一样,目的是获取补偿值并写入数字校正模块的补偿寄存器。
智能电表中常用时钟芯片中,DS3231采用的是电容式补偿,而RX-8025T及常用的SoC方案均采用数字补偿。
结合SoC方案,将数字补偿分为温度补偿和频偏补偿,提出通过最小二乘法和固化软件算法拟合晶体温度特征曲线,以达到理想的温度补偿效果。首先,对同类型、同批次或具有相同温度特征曲线的晶体振荡器进行温度补偿曲线拟合,并将拟合曲线预置到软件中;然后,采用温度传感器测取环境温度,根据温度,通过预置的拟合曲线计算补偿值;最后,将温度补偿值加上频偏补偿值,并按要求将其写入指定补偿寄存器,完成RTC校正。
3 最小二乘法拟合曲线
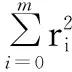
数据拟合的具体方法是:对给定数据(xi,yi)(i=0,1,…,m),在取定的函数类φ中,求p(x)∈φ,使误差ri=p(x)-yi(i=0,1,…,m)的平方和最小。即:
(1)
在几何意义上,就是寻找与给定点(xi,yi)(i=0,1,…,m)距离平方和为最小的曲线y=p(xi)。p(xi)为拟合函数或最小二乘解,该求拟合函数p(xi)的方法称为曲线拟合的最小二乘法。
假设晶体振荡器温度及时钟精度构成数据点为(Ti,Acci)(i=0,1,…,m),为所有次数不大于n(n≤m)的多项式构成的函数类,求取Pn(T)∈φ,使误差ri=P(Ti)-Acci(i=0,1,…,m)的平方和最小。

(2)
将式(2)整合到式(1),进行多项式拟合:
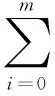
(3)
式中:I为a0,a1,…,an的多元函数。
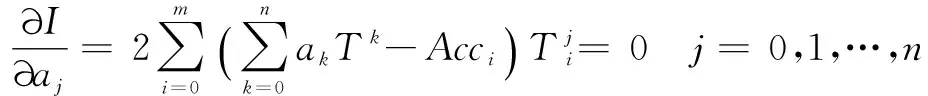
(4)
即:

(5)
式(5)是关于a0,a1,…,an的线性方程组,用矩阵表示为:

从该式中解出ak(k=0,1,…,n),代入式(2),获得温度补偿拟合曲线。
根据多项式拟合要求,先测取数据点(Ti,Acci)(i=0,1,…,m)。将数块样表放置在可设置温度(温度范围为-45~+75 ℃)的箱体中,每隔5 ℃静置不小于3h后,测取表内温度与样表在此温度下的时钟精度。为保证表内温度测量的准确性,必须使用外置温度检测电路;可使用温度芯片或高精度热敏电阻,在这采用高精度热敏电阻。为阐述补偿方法,在此仅选取一块样表进行数据分析。实际补偿中需要多组(至少5组)ak(k=0,1,…,n)拟合数据,然后对ak(k=0,1,…,n)求平均来保证拟合曲线的一致性。
假设一块样表测取的温度Ti(i=0,1,…,24)(℃)、时钟精度Acci(i=0,1,…,24)(×10-6)数据为:
Ti(i=0,1,…,24)=(-28.3,-25.5,-21.9,-18.4,-14.6,-10.4,-6.0,-1.2,3.2,7.7,12.4,16.5,21.3,26.2,31.2,36.0,41.1,45.1,50.1,55.0,59.9,65.0,69.8,74.6)
Acci(i=0,1,…,24) = (-76.39,-59.33,-42.04,-27.89,-13.59,-1.02,9.85,19.93,27.74,33.97,39.14,42.22,44.07,44.46,43.21,40.23,35.57,30.14,22.30,12.40,0.88,-12.77,-27.59,-44.59)
利用Matlab命令窗口输入Ti(i=0,1,…,24)、Acci(i=0,1,…,24);再打开曲线拟合图形用户接口,使用figure与plot(x,y,′bs′)命令拟合多项式曲线[10]。通过曲线拟合图形分析拟合多项式的合理次数[11],得到各次拟合温度补偿曲线如图2所示。
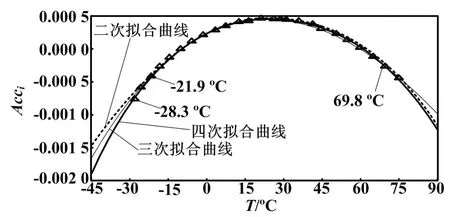
图2 各次拟合温度补偿曲线
图2显示了-45~+90 ℃温度范围内,各次曲线与实测数据之间的偏移关系。拟合的各次曲线中,在-15~+60 ℃的温度范围基本重合,故只针对各次曲线低温(小于0 ℃)和高温(大于40 ℃)不重叠部分进行分析。图中从左边第三个点即实测温度小于-21.9 ℃后,曲线开始分叉;在-25 ℃以下,拟合曲线的次数越低曲线开口上翘越厉害,表明偏离实测数据越多。比如曲线中的实测温度点-28.3 ℃,二次、三次、四次曲线拟合后的补偿值分别为-68.41×10-6、-72.11×10-6、-74.48×10-6,与理想值-76.39×10-6分别相差-7.98×10-6、-4.28×10-6、-1.91×10-6,所以二次拟合曲线在低温下存在补偿不到位的问题。图2从右边第二个点即实测温度点69.8 ℃后,曲线有略微分叉,二次、四次拟合曲线基本重合,三次拟合曲线略有上翘,故高温状态各次曲线拟合后偏离实测不明显。综合高、低温各次拟合曲线数据分析表明,四次拟合曲线最好,二次拟合曲线低温补偿不够,三次拟合曲线高温状态虽略有偏差但在可控范围内。Matlab拟合结果显示,二次、三次、四线拟合曲线残差分别为12.653 0、8.028 4、3.655 4。按园网要求,在全温度范围内误差应小于±0.5s/d,则残差不应超过5.79,即四次拟合曲线为最优,三次拟合曲线为其次。所以无论是Matlab对拟合结果的分析,还是对各次拟合曲线与实测数据点之间偏差分析都表明:四次拟合曲线为最优,三次拟合曲线其次,二次拟合曲线最差。在实际应用环境,表内温度低于-35 ℃或高于75 ℃的应用较少,且曲线次数越少,选取的测量点个数也可相应减少[11];考虑到实验室测量操作的可行性及补偿的方便性,选择三次拟合曲线。
通过Matlab拟合出式(2)的三次曲线,即n=3:
(6)
拟合结果为:a0=22.473,a1=1.996 3,a2=-0.044 777,a3=8.527 5×10-5。
为了使通过Matlab拟合得到的三次曲线能应用到软件算法,需分离出频偏补偿值与温度补偿值,即σ=σf+σt。其中:σ为需要补偿的时钟精度;σf为频偏值;σt为温度补偿值,通过曲线拟合补偿。在批量生产中,只需要拟合校正温度曲线,并在常温下校正频偏值即可。
σt=β×(T-T0)2+γ×T3
(7)
式中:σt为温度补偿值,×10-6;T0为顶点温度,℃;β为二次系数;γ为三次系数;T为检定温度,℃ 。
式(7)分解成以P3(T)相似类型的多项式,加上σf,再将同次参数一一对应于ak(k=0,1,…,3),得到式(8)。
(8)
求解式(8)即可确认参数,将参数复原到式(7),即可得到补偿方程式(9):
σ=-0.004 477×(T-22.295)2+(8.527 5× 10-5)×T3+44.72
(9)
将计算得到的数值按要求写入补偿寄存器后,便可完成时钟的补偿。
4 试验与验证
将上述最小二乘法拟合曲线方法,应用于调整低频时钟个数数字补偿方式的芯片STM32F100与调整高频时钟个数数字补偿方式的芯片SH79F642SOC。针对不同的晶体振荡器,分别选择4块样表,在-45~+75 ℃的温度范围测量秒脉冲输出误差,测试结果对比如图3所示。据测量数据分析,补偿后频率偏差均满足±0.5s/d的要求,图3中测试补偿后的秒误差数据均聚拢在±0.4s/d。对于两种不同的数字补偿方式,通过最小二乘法拟合曲线方法的补偿效果差别不大。但测试结果显示,20×10-6的晶体振荡器比5×10-6的效果更佳。图3(b)表明高温70 ℃以上,补偿后时钟精度时钟误差绝大值大于0.3s/d;而图3(c)中,温度范围聚拢在±0.3s/d。

图3 晶振曲线拟合后测试结果对比图
5 结束语
智能电表等自动化仪表有低功耗及高时间精度的要求。为降低系统功耗,常选择音叉型低频晶体振荡器(32 768 Hz)作为RTC时钟源,但此晶体振荡器温度特性曲线表现为抛物线,在全温度范围内很难满足时间精度要求,所以需进行温度补偿。在智能电表中,应采用最小二乘法拟合温度补偿曲线方法对温度引起的频率偏差进行补偿。通过验证与分析,使用三次曲线拟合温度补偿曲线方法,进行RTC全温度范围补偿,能完全满足智能电表中要求RTC频率偏差为±0.5 s/d的要求,并且能在全温度范围-45~+75 ℃内达到±0.5 s/d的计时误差。根据二次、三次、四次曲线拟合结果分析,次数越高补偿效果越佳;要想获得更高精度,理论上四次曲线拟合效果更佳,但其软件算法的实现更复杂,故可根据实际应用需要选择。最小二乘法拟合温度补偿曲线的方法不仅可以应用于智能电表,也可以应用于对RTC有时钟精度要求的其他仪器仪表。
[1] 范爽.石英晶体振荡器的温度补偿技术[D].天津:南开大学,2014.
[2] 徐磊.一种高精度温度补偿晶体振荡器的算法研究及电路实
现[D].西安:西安电子科技大学,2014.
[3] 邹云.温度补偿晶体振荡器的研究[D].天津:南开大学,2010.
[4] 刘会娟,伍冬,郑德平,等.一种高精度模数混合温度补偿晶体振荡器[J].微电子学,2011,41(6):830-839.
[5] 白丽娜,周渭,李婉莹,等.基于应力处理的温度补偿石英晶体振荡器[J].仪器仪表学报,2014,35(7):1594-1598.
[6] 赵东艳,周芝梅,王于波,等.一种基于累积误差控制的RTC补偿算法及电路[J].电子技术应用,2014,40(12):66-68.
[7] 梁世清,包海泉,季海涛,等.内置RTC作为电能表计时钟的应用[J].自动化仪表,2012,33(1):76-78.
[8] 周宣,任智仁,李宏华,等.智能电能表硬件RTC误差补偿系统:202256438U[P].2012-05-30.
[9] 唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现代化,2008(6):15-19.
[10]赵海滨.MATLAB应用大全[M].北京:清华大学出版社,2012.
[11]陈岚峰,杨静瑜,崔崧,等.基于MATLAB的最小二乘曲线拟合仿真研究[J].沈阳师范大学学报(自然科学版),2014,32(1):76-79.
Application of the RTC Compensation Based on Least Square Curve Fitting for Smart Meters
WANG Yueping1,ZHANG Daozhen2,QIU Yubao1
(1.Holley Technology Co.,Ltd.,Hangzhou 310023,China;2.Wanxiang A123 System Asia Co.,Ltd.,Hangzhou 311215,China)
Driven by the requirements of the cost reduction and higher efficiency,the System-on-a-Chip (SoC) scheme has been adopted gradually for MCU of the smart meters,and on the basis of the development of integrated electronic technology,the multi-component integration is the trend.At present,most of the built-in real time clock (RTC) modules of SoC need clock compensation for meeting the accuracy requirement of ±0.5 s/d for the State Grid;aiming at this issue,the strategy of temperature compensation for RTC is proposed;with this strategy,temperature is detected by using hardware,and the least square curve fitting for temperature characteristics of the crystal oscillator is used in software.Combining with Matlab least squares curve fitting tool,data analysis and research are conducted,by using cubic curve fitting compensation curve,and by test and verification that this method can reach the demand of ±5 s/d system accuracy between temperature -45 ~ +75 ℃.Batch verification of this method has been passed;the accuracy of the clock in new generation of smart meters can be fully satisfied,which provides a new concept and direction in selecting RTC scheme for smart meters and other automation instruments.
Energy; Electric power; Smart meter; Least square method; Temperature compensation; Matlab; Accuracy
王岳平(1982—),女,硕士,工程师,主要从事智能电表、配网故障指示器的研究。E-mail:yueping870@163.com。
TH-39; TP216
A
10.16086/j.cnki.issn1000-0380.201704019
修改稿收到日期:2016-11-21
