一个基于卷积稀疏表示的图像重构算法*
2017-04-24陈小陶许道云
陈小陶 许道云
(1.贵州大学数学系 贵阳 550025)(2.贵州大学计算机科学系 贵阳 550025)
一个基于卷积稀疏表示的图像重构算法*
陈小陶1许道云2
(1.贵州大学数学系 贵阳 550025)(2.贵州大学计算机科学系 贵阳 550025)
在利用稀疏表示技术重构图像的应用中,传统的方法是独立地计算一组重叠的图像块,在表示中只针对每个图像块进行单独稀疏编码。利用卷积稀疏表示,可以将整个图像看做是一个整体,对其进行稀疏编码,由滤波器字典与相应特征响应的卷积总和代替传统的字典矩阵与编码系数的乘积对图像进行分解。论文基于卷积稀疏表示方法,提出一个图像重构算法,利用交替方向乘法器方法(ADMM)对输入图像进行稀疏逼近,得到特征响应系数,达到对图像卷积分解的目的。实验结果说明卷积分解机制稀疏性能较优,更适合于图像重构。
稀疏表示; 卷积稀疏表示; ADMM; 图像重构
1 引言
稀疏表示(Sparse Representation)[1~2]是通过用尽可能少的原子系数线性表示原始信号,它与压缩感知(Compressed Sensing)[3~4]有着直接的联系。压缩感知提出如果一个信号是稀疏的或者压缩的,原始信号可以通过这些少量的测量值进行重构。信号可以稀疏表示是压缩感知的先验条件,由字典矩阵依据稀疏度量标准求解变换后得到的稀疏向量再通过逆变换从而实现信号的精确重构或近似重构。由字典矩阵依据稀疏度量标准求解变换后得到的稀疏向量求解变换的过程在稀疏表示中叫做稀疏分解。依据压缩感知中的重构原理,可以先通过稀疏分解得到稀疏系数,再通过逆变换重构图像。
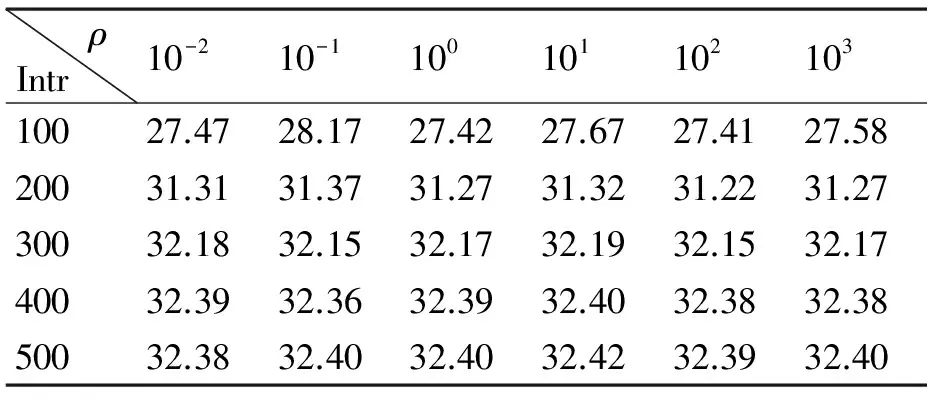
稀疏分解问题是指,在字典张成的整个信号空间下,依据稀疏度量标准寻找信号的最优解,即稀疏优化。典型稀疏度量标准包括l0范数、l1范数、l2范数以及lp(0 虽然基于传统的稀疏表示方法可以大大减小问题的计算,也获得了很好的效果,但是以往的研究通常是独立地处理重叠块,最后通过平均每一块之间的重叠像素来获得结果。因为这种处理方法使得每个像素的输出图像将被估计更多次,所以相邻的块之间的重叠像素将提供更好的重构结果。然而,在解决块估计问题时,这种“重叠平均”机制忽略了一个重要的约束,重叠区域中的像素相邻的块应该是完全一样的,即一致性。一致性约束提供了在处理每一个单一的估计问题的先验信息。最近,文献[11]提出了一种聚合方法,以减轻重叠块之间的不一致,并在图像恢复方面取得了较好的效果。然而,对于图像重构方面,仍需要更好的方法证明一致性约束的重要性。 因为图像块之间的一致性,2010年,Zeiler在文献[12]最早提出卷积稀疏表示,利用带卷积的稀疏编码实现稀疏表示整个图像,即利用滤波器与相应特征响应的卷积总和,代替传统的字典矩阵与编码系数的乘积对信号进行分解。同年,文献[13]提出用卷积匹配追踪算法训练深层卷积网络。2014年,文献[14]提出用交替方向乘法器的方法(ADMM)进行卷积分解,通过滤波器与对应特征响应做卷积,减少相邻位置图像块的编码冗余度。尽管这些算法用来解决卷积稀疏表示问题,但很少注意验证卷积稀疏表示在图像重构方面优于传统的基于块的稀疏表示。 针对传统的稀疏表示算法一般只是对图像块进行单独编码,而忽略图像的整体性,本文构建了一个基于卷积稀疏表示的重构算法,以此验证应用一致性约束对整幅图像进行分解优于传统的稀疏编码。用交替方向乘法器方法(Alternating Direction Method of Multipliers,ADMM)对输入图像进行卷积稀疏分解。带卷积的ADMM算法根据卷积独有的性质,只需要一个卷积核,就可表示图像任意位置的相同特征,即能够用较少的原子个数有效刻画图像的几何特征。通过实验验证与传统的稀疏表示模型相比,卷积分解机制更适合于图像重构。 基于传统的稀疏表示一幅图像s,由字典矩阵与编码系数的线性结合对图像进行分解。其数学表达式为 (1) 式中D表示字典矩阵,x表示稀疏系数,s表示原图像,λ表示正则化参数,用来调整正则化程度。这种传统的基于块的稀疏编码方式在图像处理方面应用广泛。 但是,在传统意义上的稀疏表示模型中,还存在一些缺陷。如l0范数的可拓展性贫乏,在处理大规模问题上限制了稀疏编码的应用。为了减少建模和计算负担,一般都只是对图像块单独编码。其次,只针对一维信号进行单独编码,忽略了数据信息二维空间结构和图像块之间的一致性,导致编码高度冗余。这种稀疏表示方法忽视了图像块之间的一致性,现有的聚合和平均策略只能缓解由此带来的问题。 考虑到图像块之间的一致性,2010年,文献[11]提出利用带卷积的稀疏编码实现稀疏表示整个图像,即利用滤波器与相应特征响应的卷积总和,代替传统的字典矩阵与编码系数的乘积对信号进行分解。利用正则化公式表示该模型: (2) 其中{dm}是一组滤波器构成的M维卷积字典,每个滤波器的大小为n×n,⊗表示卷积符号,{xm}是一组特征响应,每个特征响应的大小与s相同,s表示输入图像,为了表示上的方便s和xm为N维向量,N是图像中像素的个数。在这个带卷积的稀疏表示模型中,充分考虑了图像块之间的相关性。本文将基于这个模型,构建一个图像重构算法,并与传统的基于块的稀疏表示重构图像进行比较。 带卷积的稀疏表示模型,对应的正则化问题可以表示为式(2)。式(2)利用一种图像先验,即对整幅图像变换稀疏性。引入辅助变量{ym}(其中{ym}也是一个维向量)式(2)变换成: s.t.xm-ym=0, ∀m (3) 再利用对偶变量,引入拉格朗日乘子u,则约束优化问题式(3)变为非约束等价形式: (4) 式中ρ是一个正则化参数。 本文用交替方向乘法器(ADMM)求解式(4)描述的优化问题,交替方向乘法器是一种对偶凸优化算法,其可以将可分结构的凸规划问题分解为若干子问题交替地求解[15]。依据交替方向乘法器的运算规则将本文中求解式(4)分为三个子问题,步骤如下: 1) 固定特征响应系数{xm},乘子u,更新辅助变量{ym}。 (5) 式(5)为典型的l1范数优化问题,处理该问题较常用的方法是阈值法,采用阈值法可得: (6) 式中shrink(.,.),表示软阈值函数,定义为 shrink(g,u)=sign(g)max{0,|g|-u} (7) 2) 固定辅助变量{ym},乘子u,更新特征响应系数{xm}。 (8) 3) 按照ADMM算法规则更新乘子u。 (9) 在求解这些子问题的时候,最大的计算代价是在求解式(8)中也就是更新特征响应系数,接下来本文具体介绍求解子问题2)。表示如下: (10) 下面详细介绍子问题2)的求解: 在子问题2)中,出现了卷积的求解,又卷积定理[16]表明了两个傅里叶变换之间的关系构成了空间域和频率域之间的基本关系,即一个域中卷积对应于另一个域中的乘积,也就是说可以将卷积运算转变成乘积运算。从而在求解子问题2)时,首先应用DFT(离散傅里叶变换)卷积定理,将离散的卷积运算转换成乘积运算。 (11) (12) 从而式(11)的问题可以表示为 (13) (14) (15) 基于上述讨论,本文引入一个图像重构算法,称为CSR_ADMM算法,具体步骤如下: 输入:样本s,滤波器字典{dm},参数λ,ρ。 初始化:{ym}={um}=0。 步骤1:通过引进辅助参数的拉格朗日函数,构建问题(2)的限制最优化问题; 步骤5:通过式(6)更新{ym}; 步骤6:通过式(9)更新{um}; 步骤7:重复步骤2~6。 在卷积稀疏表示模型下,应用上述的CSR-ADMM算法,计算出图像的特征响应系数,并利用得到的特征响应系数重构图像,与基于传统的稀疏表示算法ADMM得到的稀疏系数重构图像的峰值信噪比进行比较。 在实验中,卷积分解机制使用一组12×12×36的滤波器字典[17],其中λ=0.01,ρ=2,迭代次数为500次。传统分解机制使用一个64×256的DCT字典,λ=0.01,迭代次数同为500次,输入图像采用标准图像lena,house,peppers,bird,city,fruits(大小均为512×512),作为测试图像。 图1 原始图像 图2 基于卷积稀疏表示重构图像 其中图1表示上述六幅标准图像的原始图像,图2表示基于卷积分解机制的重构图像,图3表示传统基于块的稀疏分解机制的重构图像。表1给出了针对不同的测试图像,基于带卷积的与传统的基于块的稀疏分解机制下优化算法重构图像的峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)。 图3 基于传统稀疏表示重构图像 表1 基于不同分解机制下的重构图像峰值信噪比(PSNR)[dB] 从表1中它们的均值可以看出,带卷积的ADMM重构图像峰值信噪比不带卷积基于块的提高了7.49dB。由此,说明在带卷积的稀疏表示模型下,稀疏表示性能更优,卷积分解机制更适合图像重建。 为了进一步说明卷积分解机制更适合于图像重构,表2给出了在标准图像lena(512×512)下,当λ=0.01固定时,针对不同的迭代次数与不同的ρ的取值CSR_ADMM重构图像峰值信噪比的对比。 表2 基于不同的迭代次数与ρ的取值CSR_ADMM重构图像PSNR[dB] 从表2可以看出,当ρ的取值固定时,随着迭代次数的增加,图像的峰值信噪比也在增加,当迭代次数固定时,ρ的值从变化10-2到103图像的峰值信噪比基本没有改变。从表2也可以看出当迭代次数为200时,基于卷积的稀疏分解机制得到的图像峰值信噪比,比传统的稀疏分解机制在迭代500次时高。这也充分说明,基于卷积的稀疏分解机制得到的特征响应系数优于传统的稀疏分解机制。 本文基于卷积稀疏表示模型,利用ADMM将其分解为几个简单的非约束优化子问题,从而得到特征响应系数。卷积稀疏表示直接把整个图像进行滤波,充分考虑了重叠图像块像素之间的一致性,较之前传统的基于块的稀疏表示,卷积分解机制可以保持特征响应中输入信号的空间信息,进而达到较优的稀疏逼近,更有利于对图像进行重构。下一步可将本文的CSR_ADMM优化算法应用于图像去噪,图像超分辨率等问题。 [1] Elad M, Figueiredo M A T, Ma Y. On the role of sparse and redundant representations in image processing[J]. Proceedings of the IEEE,2010,98(6):972-982. [2] Cheng H, Liu Z, Yang L, et al. Sparse representation and learning in visual recognition: Theory and applications[J]. Signal Processing,2013,93(6):1408-1425. [3] Donoho D L. Compressed sensing[J]. Information Theory, IEEE Transactions on,2006,52(4):1289-1306. [4] Baraniuk R G. Compressive sensing[J]. IEEE signal processing magazine,2007,24(4):118-121. [5] Figueiredo M A T, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. Selected Topics in Signal Processing,2007,1(4):586-597. [6] Kim S J, Koh K, Lustig M, et al. An interior-point method for large-scale-regularized least squares[J]. IEEE journal of selected topics in signal processing,2007,1(4):606-617. [7] Yang J, Zhang Y. Alternating direction algorithms for l1-problems in compressive sensing[J]. SIAM journal on scientific computing,2011,33(1):250-278. [8] Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. Signal Processing, IEEE Transactions on,1993,41(12):3397-3415. [9] Engan K, Aase S O, Hakon Husoy J. Method of optimal directions for frame design[C]//Acoustics, Speech, and Signal Processing,1999:2443-2446. [10] Zhang Z, Xu Y, Yang J, et al. A survey of sparse representation: algorithms and applications[J]. Access, IEEE,2015,3:490-530. [11] Kervrann C. PEWA: Patch-based Exponentially Weighted Aggregation for image denoising[C]//Advances in Neural Information Processing Systems,2014:2150-2158. [12] Zeiler M D, Krishnan D, Taylor G W, et al. Deconvolutional networks[C]//Computer Vision and Pattern Recognition(CVPR),2010:2528-2535. [13] Szlam A, Kavukcuoglu K, LeCun Y. Convolutional matching pursuit and dictionary training[J/OL]. [2010-10-3]. http://arXiv.org/abs/1010.0422. [14] Wohlberg B. Efficient convolutional sparse coding[C]//International Conference on Acoustics, Speech and Signal Processing(ICASSP),2014:7173-7177. [15] Gabay D, Mercier B. A dual algorithm for the solution of nonlinear variational problems via finite element approximation[J]. Computers & Mathematics with Applications,1976,2(1):17-40. [16] 杨帆.数字图像处理与分析[M].北京:北京航空航天大学出版社,2010:39-44. YANG Fan. Digital Image Processing and Analysis[M]. Beijing: Beijing University of Aeronautics and Astronautics Press,2010:39-44. [17] Wohlberg B. Convolutional sparse representation of color images[C]//Southwest Symposium on Image Analysis and Interpretation(SSIAI),2016:57-60. Image Reconstruction AlgorithmBased on Convolution Sparse Representation CHEN Xiaotao1XU Daoyun2 (1. Department of Mathematics, Guizhou University, Guiyang 550025)(2. Department of Computer Science, Guizhou University, Guiyang 550025) In the application of sparse representation in image reconstruction, the traditional method is to compute a set of overlapping image blocks independently. Using convolution sparse representation, the whole image is seen as a whole, the of sparse coding and by the filter dictionary and corresponding characteristic response of the convolution sum instead of the product of traditional dictionary matrix and coding coefficients for image decomposition. In this paper, based on the sparse representation model of convolution, an image reconstruction algorithm is proposed, the input image is approximated by the alternating direction multiplier method(ADMM), and the characteristic response coefficient is obtained. The experimental results show that the sparse performance of the convolution decomposition mechanism is better, and it is more suitable for image reconstruction. sparse representation, convolution sparse representation, ADMM, image reconstruction Class Number TP391 2016年10月5日, 2016年11月26日 国家自然科学基金(编号:61262006)资助。 陈小陶,女,硕士研究生,研究方向:密码学理论与工程。许道云,男,博士,教授,博士生导师,研究方向:SAT问题、可计算性与计算复杂性、算法设计与分析等。 TP391 10.3969/j.issn.1672-9722.2017.04.0292 卷积稀疏表示
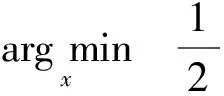

3 带卷积的ADMM算法
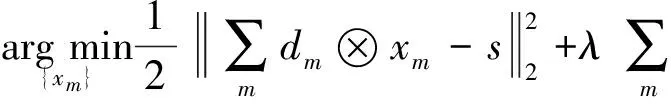

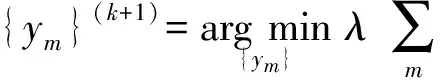




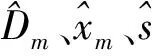
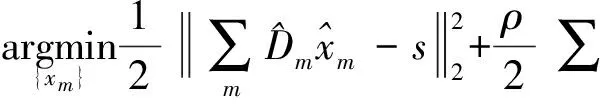


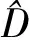
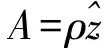
4 实验分析




5 结语
