海上LF油田水平井生产过程中井壁稳定性问题研究

范志利，朱磊，曹砚锋，文敏，王彬

(中海油研究总院，北京 100028)

海上LF油田水平井生产过程中井壁稳定性问题研究

范志利，朱磊，曹砚锋，文敏，王彬

(中海油研究总院，北京 100028)

随着海上油气田的进一步开发，海上已经针对低渗透油气田进行了开采，目前海上LF等多个低渗透油气田已经进行开发，这些区块储层砂岩岩石强度属于中-高强度，其生产过程中的井壁稳定问题直接影响着完井方式及后期的开发方式。针对海上LF中高强度砂岩油田水平井生产过程中的井壁问题展开研究，通过数值模拟的方法，利用等效塑性应变理论，对水平井在生产过程中影响井壁稳定的因素(生产压差、地层出水、地层压力衰减)进行研究。研究结果也表明，水平井井眼沿最小主应力方向时，且在纯砂岩地层中时可以采用裸眼完井，与油田实际生产的情况相符，从而验证了该方法的可行性。研究结果可对油田进行完井方法优选以及后期作业提供指导。

水平井； 生产过程；井壁稳定；中高强度砂岩

目前海上低渗透油气田已经进行开发，这些区块储层砂岩岩石强度属于中-高强度，通过对中-高强度低渗透油气藏砂岩储层在生产过程中的井壁稳定性进行研究，给低渗透砂岩油气藏完井方法以及后期开发过程中采取的措施提供依据。

对于砂岩地层的井壁稳定性的研究主要有3种方法：

1)以弹性力学为基础，推导出井壁周围的应力分布状况，然后使用摩尔-库伦强度准则或者D-P准则作为判定依据，分析井壁稳定性。

2)以弹塑性力学为基础，在假设两个水平地应力相等的前提下，根据应力-应变理论，推导直井井眼处井壁周围的应力分布状况，然后使用最大剪应力准则作为判定依据，分析井壁稳定性。

3)以数值模拟为手段，建立弹塑性模型，采用等效塑性应变力理论，使用D-P准则作为判断依据，对井壁稳定性进行分析。

对井壁稳定性的研究主要是基于孔弹性理论，通过有效应力理论和岩石力学理论，应用弹性力学的方法预测坍塌压力。邓金根[1]和Adnoy等[2]根据弹性力学，推导出直井和斜井井壁应力分布公式，根据摩尔-库伦强度准则得到井壁坍塌压力。Mclean等[3]比较分析了不同强度准则对坍塌条件的影响。用弹性力学公式和强度准则确定的坍塌压力，是将岩石假设成弹性材料，认为岩石强度达到屈服极限时，即发生坍塌。丰全会等[4]、殷有泉等[5]采用稳定性理论和方法研究井壁坍塌问题，利用弹塑性分析，求其了直井钻井过程中坍塌压力的弹塑性解析解，但是该方法是将井眼简化为平面应变问题，并假设了水平向最大主应力和水平最小主应力相等为前提条件，对于水平向两个主应力不相等的情况还需要运用数值模拟的方法进行计算。熊友明等[6]利用C公式对井壁稳定性进行判断，但是C公式只考虑了垂向应力的影响。练章华等[7,8]利用等效塑性应变理论，采用有限元数值模拟的方法，对井眼周围的应力进行了研究分析。周长江等[9]、兰凯[10]等也利用等效塑性应变理论采用数值模拟的方法对砂岩地层和灰岩地层的井壁稳定问题进行了分析研究。在对井壁坍塌压力进行计算时，通常采用摩尔-库伦强度准则和D-P准则进行计算，摩尔-库伦强度准则在计算地层坍塌压力的时候，只考虑的最大主应力和最小主应力，而忽略了中间主应力的影响，而D-P准则则考虑了中间主应力的影响，因此摩尔-库伦强度准则计算的结果比D-P准则计算的结果保守[11]。根据李军等[12]通过使用三维弹塑性有限元模型研究发现，在相同载荷的情况下，弹塑性岩石比脆性岩石更稳定，同时使用弹塑性模型计算的值比弹性条件下计算的结果更稳定。

实际上，地层岩石为弹塑性材料，通常情况下地层发生失稳的过程是地层岩石先发生弹性形变，之后进入塑性形变阶段，当塑性形变达到一定的值时，地层发生失稳。因此，从现有理论和已有的研究情况看，对于砂泥岩地层坍塌压力的预测，采用弹性力学基础上计算的值较弹塑性力学基础上计算的值更为保守，而采取D-P准则作为判据的计算结果与实际情况更为接近。

1 理论基础

由等效塑性理论可知，井壁失稳是由于井周地层受力平衡状态被打破，井壁岩石发生塑性屈服，当塑性屈服值超过井壁岩石临界塑性屈服值时，井壁发生失稳。其中，井周地层岩石发生塑性变形可由下式Drucker-Prager准则进行判定:

J2=H1+H2×J1

(1)

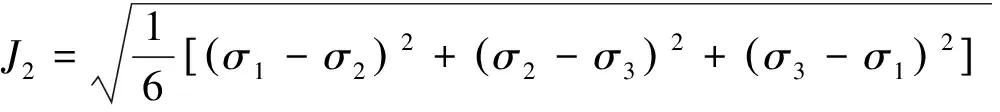
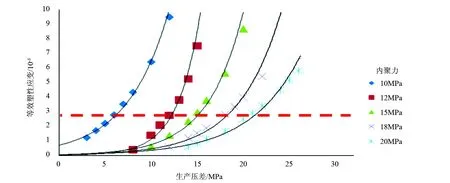
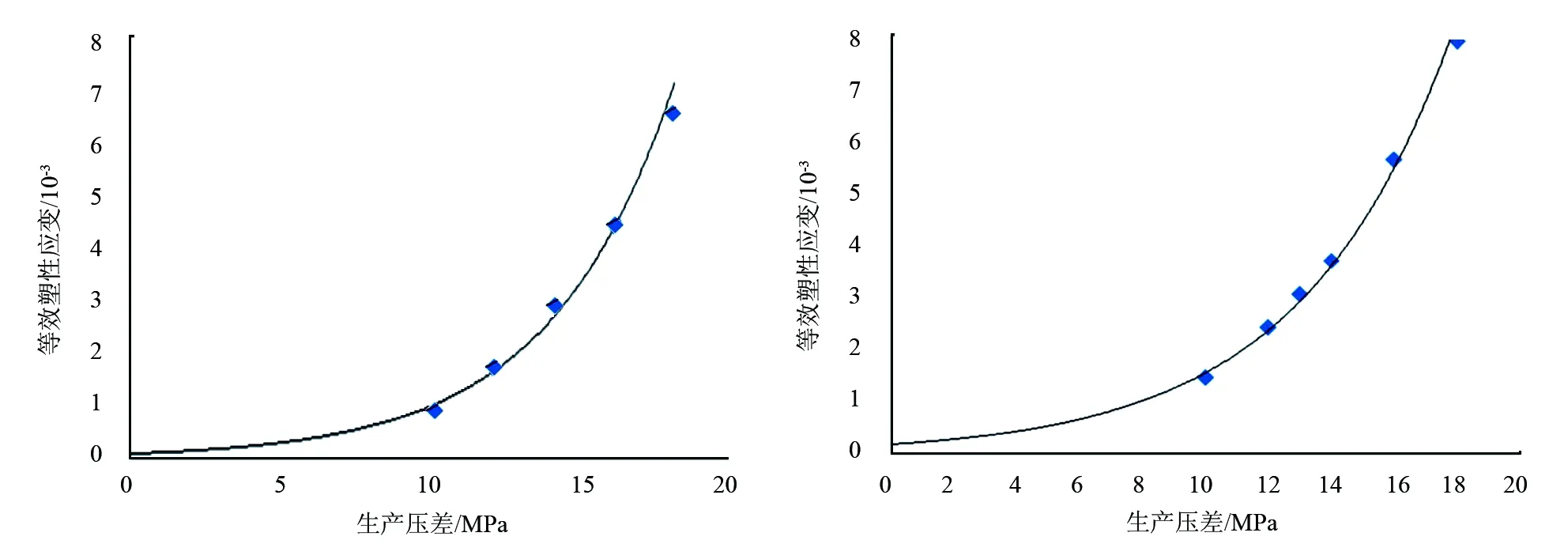
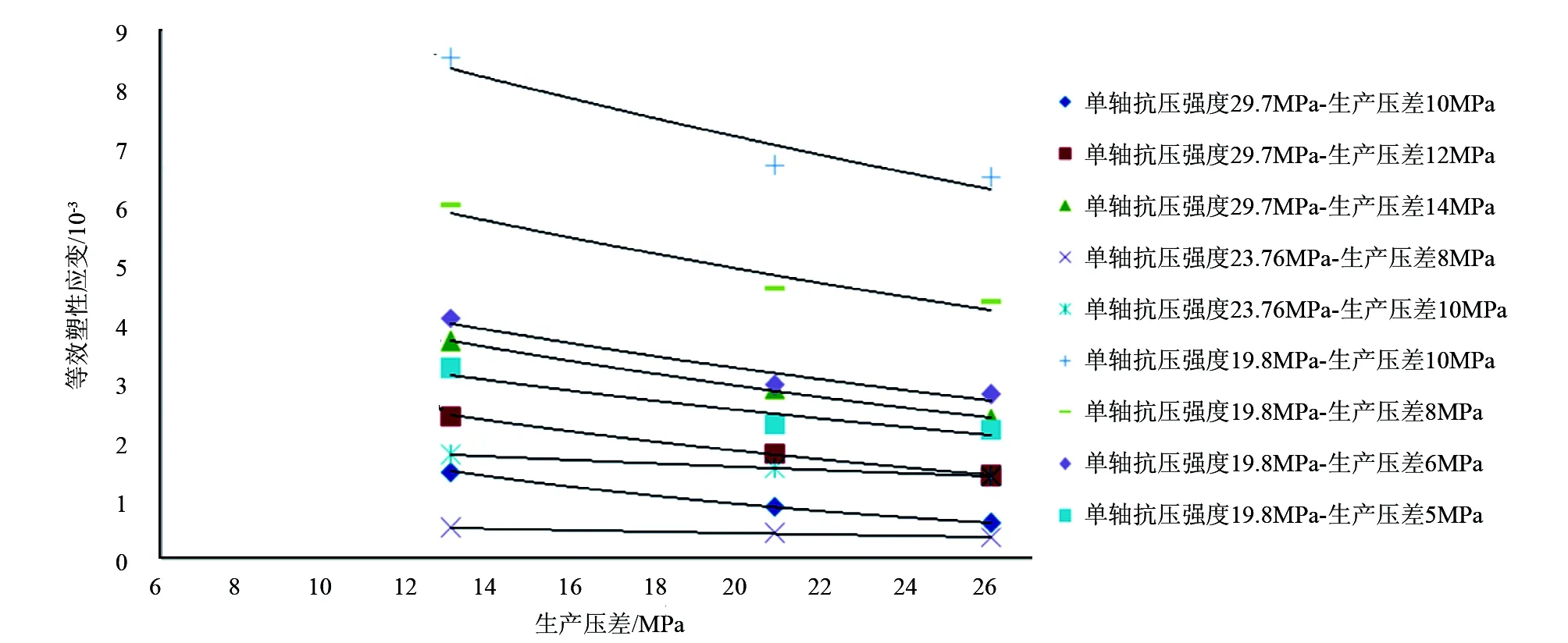
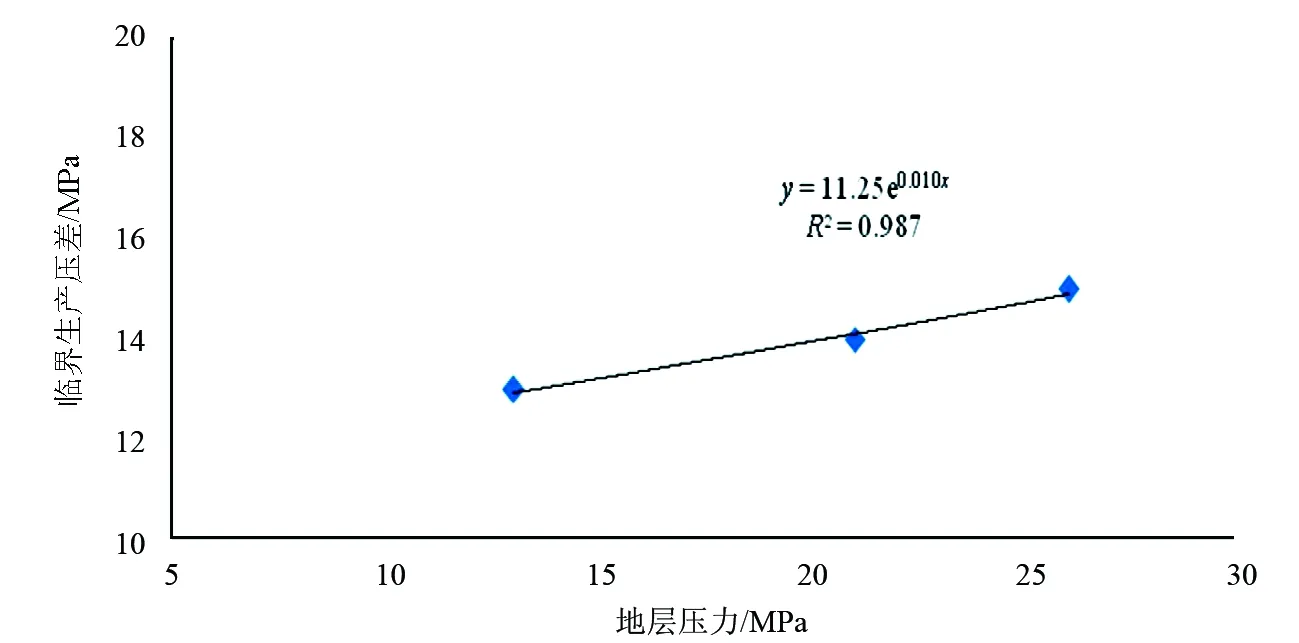
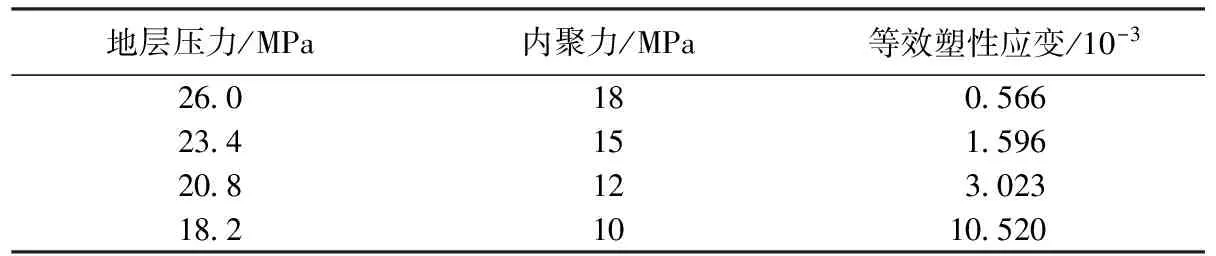
当J2>H1+H2×J1时，井壁稳定；当J2

根据等效塑性应变准则，井周地层岩石进入塑性屈服后，当其等效塑性应变εp大于岩石所允许的等效塑性应变临界值εc时，地层将发生破坏失稳，可由下式进行描述求解：

εp>εc

(2)

(3)

式中：εp1、εp2、εp3分别为3个主应力方向的塑性应变，1。

大量的研究表明，不同的地层岩石，具有不同的等效塑性应变临界值，其分布通常为0.3%～0.8%[13～15]。当地层岩石等效塑性应变超过这一临界值时，地层将发生破坏失稳。

而弹性理论认为，当材料达到最大屈服应力值时材料即失稳，而地层岩石为弹塑性材料，当材料达到最大屈服应力值时，材料仍然保持稳定，此时地层岩石进入塑性屈服阶段，只有塑性应变达到一定值时，地层岩石才发生失稳。因此，采用弹塑性模型结合等效塑性应变理论计算的井壁稳定性更接近真实情况。

2 建立模型(水平井模型)

根据前面研究分析的结果，模型的建立主要考虑以下因素：

1)井眼尺寸8.5in。

2)井眼延伸方位与水平向最小主应力一致。

3)弹塑性模型。

4)D-P判断准则。

5)等效塑性应变取值0.3%。

研究条件：①通过研究岩石强度变化与井壁稳定性之间的关系，来间接反映出水对井壁稳定性的影响；②研究地层压力衰减与井壁稳定关系。

3 实例分析

根据室内试验获得了研究区块的地质力和岩石强度参数，见表1。采用表1中的数据对生产过程中井壁稳定性展开研究。

表1 地质力学和岩石强度参数表

表2 地层出水岩石强度降低后的参数

3.1 地层出水对井壁稳定性的影响

地层出水后，储层砂岩黏土矿物会发生吸水膨胀，导致岩石强度降低。通过研究得到研究区块的岩石强度参数如表2所示。根据表2中的数据，建立的模型，内聚力为18、15、12、10MPa时分别对应的单轴抗压强度为35.60、29.70、23.76、19.80MPa，计算结果见图1和图2，图1为不同内聚力时，生产压差与等效塑性应变关系图，图2为不同生产压差下，内聚力与等效塑性应变关系图。

图1 生产压差与井眼等效塑性应变图

图2 内聚力与井眼等效塑性应变图

当内聚力(即单轴抗压强度)一定时，等效塑性应变与生产压差成指数关系，而当生产压差一定时，等效塑性应变与内聚力成指数关系。当等效塑性应变为0.003时，井壁失稳，故认为该时对应的生产压差为临界生产压差，从图1中可以看出，水平井临界生产压差随岩石内聚力的增大而增大，同时在红色虚线以下的生产压差和内聚力时，均可以保持井壁的稳定。单轴抗压强度为29.70、23.76、19.80MPa(即内聚力为15、12、10MPa)时的临界生产压差分别为15、12、6MPa。因此当水平井裸眼生产时，在当前地应力条件下，如果地层压力不变且生产过程中，生产压差不超过6MPa，则地层稳定，可采用裸眼完井。

从图2中可以看出，在当前地应力条件下，如果地层压力不变，当生产压差保持12MPa时，随着地层出水，岩石强度的降低，井壁等效塑性应变逐渐增大，当地层岩石单轴抗压强度降低到23.76MPa(即内聚力为12MPa时)，井壁等效塑性应变增大到2.967×10-3，此时如果地层岩石强度继续降低，则井壁将会发生失稳。

3.2 地层压力衰减对井壁稳定性的影响

随着油气层开采时间的增加，地层压力逐渐减低，当地层压力降低5MPa和13MPa时，分析地层压力衰减对井壁稳定的影响。

3.2.1 地层压力降低5MPa时，井壁稳定性分析

地层压力降低5MPa时，不同生产压差下的等效塑性应变如图3所示。地层压力降低后，井壁等效塑性应变随生产压差的增大而增大，即井壁稳定性随生产压差的增大而减弱。当生产压差为14MPa时，井壁等效塑性应变为2.888×10-3，在该情况下，如果生产压差继续增大，则井壁会发生失稳，因此如果地层压力降低5MPa，生产压差不大于14MPa时，可采用裸眼完井。

3.2.2 地层压力降低13MPa时，井壁稳定性分析

地层压力降低13MPa时，不同生产压差下的等效塑性应变如图4所示。当生产压差为13MPa，此时井壁等效塑性应变为3.069×10-3，地层进入失稳阶段。因此如果地层压力降低13MPa之后，生产压差小于13MPa，可采用裸眼完井。

图3 地层压力降低5MPa时，不同生产压差下的 图4 地层压力降低13MPa时，不同生产压差下的 井壁等效塑性应变 井壁等效塑性应变

根据以上的分析方法又计算了生产压差一定时，单轴抗压强度为23.76、19.8MPa(内聚力为12、6MPa)时，地层压力衰减对井壁稳定的影响，见图5。在相同岩石强度、地应力条件和生产压差不变的条件下，井壁等效塑性应变随地层压力的减小而增大，且两者成指数关系。单轴抗压强度为23.76MPa的岩石，在地层压力减小13MPa时，临界生产压差为11MPa；单轴抗压强度为19.8MPa的岩石，在地层压力减小13MPa时，临界生产压差为4.5MPa。

相同压差时，地层压力与临界生产压差的关系见图6，临界生产压差与随着地层压力成指数关系，随着地层压力的减小而减小。因此，为保证水平井生产过程中井壁稳定性，临界生产压差随地层压力的减小而进行调整。

图5 井壁等效塑性应变随地层压力变化关系图

图6 地层压力与临界生产压差的关系图

3.3 地层压力衰减与地层出水共同作用对井壁稳定性影响分析

地层压力衰减和地层出水(即地层岩石强度减小)共同作用，按以下情况考虑：①假设地层压力从原始地层压力降低至18.2MPa，每降低2.6MPa取一个点进行计算；②在地层压力降低的过程中，生产压差保持不变，假设为12MPa。计算结果见表3。

地层压力降低与地层出水(即岩石强度降低)同时作用时，等效塑性应变值随两者的减小而增大，

表3 地层压力衰减和岩石强度降低共同作用时的等效塑性应变

即井壁的不稳定性增加。当生产压差为12MPa，地层压力降低5MPa时且岩石强度内聚力降低到12MPa时，地层等效塑性应变为3.023×10-3，即地层发生失稳。

4 结论和建议

1)在地层压力和地应力条件及岩石强度不变的情况下，等效塑性应变值与生产压差呈指数关系，即随着生产压差的增大，井壁等效塑性应变值逐渐增大，井壁稳定性变差；随着地层出水时间的增加，地层岩石强度降低，井壁稳定性逐渐减弱，为了保持井壁的稳定，则需要降低生产压差。

2)在地层压力不变，上覆应力>水平最大地应力>水平最小地应力时，生产过程中临界生产压差随着地层在地层岩石强度的减小而降低，如果岩石单轴抗压强度降低46%，且整个生产周期中生产压差不大于6MPa时，则可以采用裸眼完井。

3)研究结果与实际生产情况相符，说明该方法用来计算生产过程中井壁稳定性的可行性，因此，可以采用该方法优化LF地区的完井方法并对后期作业提供指导。

4)如果水平井井眼沿最小主应力方向，且在纯砂岩地层中，则可以采用裸眼完井，采用数值模拟方法计算要求井眼处于纯砂岩段地层。因此，这对于定向钻井过程中水平井井眼轨迹控制的要求较高。

[1]邓金根.泥页岩井眼力学稳定理论及工程应用[D].北京:石油大学(北京),2000.

[2]Adnoy B S, Rogaland U,Chenevert M E.Stability of highly inclined boreholes[J].SPE1605,1987.

[3]Mclean M R ,Addis M A. Wellbore stability:the effect of strength criteria on mud weight recommendations[J].SPE20405，1990.

[4]丰全会，程远方，张建国.井壁稳定的弹塑性模型及其应用[J].石油钻探技术,2000,28(4):9～11.

[5]殷有泉，陈朝伟.用稳定性理论和方法研究井壁坍塌问题[J].北京大学学报(自然科学版),2009,45(4):559～564.

[6]熊友明，潘迎德.产层岩石坚固程度判断指标“C”公式及其应用[J].西南石油学院学报,1994,16(2):67～73.

[7]练章华，杨龙，段永刚，等.塑性应变准则在油井出砂预测中的应用[J].西南石油学院学报,2003,25(4):16～18.

[8]吴欣袁，练章华，林铁军，等.分支井连接段有限元建模与分析[J].西南石油学院学报(自然科学版),2012,34(2):56～62.

[9]周长江，刘向君，张卓，等.水平气井井壁稳定性研究[J].天然气工业，2006，26(8)：81～82.

[10]兰凯，熊友明，闫光庆，等.川东北水平井储层井壁稳定性及其对完井方式的影响[J].吉林大学学报(地球科学版)，2011，41( 4)：1233～1238.

[11]李天太，孙正义.井壁失稳判断准则及应用分析[J].西安石油学院学报(自然科学版),2002,17(5)：25～27,49.

[12]李军，陈勉，金衍，等.大位移井井壁稳定三维弹塑性有限元分析[J].岩石力学与工程学报,2004,23(14)：2238～2389.

[13]刘向君，罗平亚.岩石力学与石油工程[M].北京:石油工业出版社，2004.

[14]陈勉，金衍，张广清.石油工程岩石力学[M].北京:科学出版社，2008.

[15]Kiorholt H, Jor anson H. Advanced sand prediction in a user friendly wrapping[J].SPE 47333,1998.

[编辑] 帅群

2016-10-24

国家科技重大专项(2011ZX05024-003)。

范志利(1981-)，男，硕士，工程师，现主要从事钻完井设计工作，fanzhl@cnooc.com.cn。

TE257

A

1673-1409(2017)7-0056-06

[引著格式]范志利，朱磊，曹砚锋，等.海上LF油田水平井生产过程中井壁稳定性问题研究[J].长江大学学报(自科版), 2017,14(7):56～61.