基于Bayesian理论的无参考信号主动Lamb波损伤定位方法
2017-04-21尹涛缪傲王祥宇
尹涛 缪傲 王祥宇


摘要:目前主动Lamb波损伤检测方法大都基于健康状态下的参考信号以获取损伤散射信号,并采用确定性的方法进行损伤定位,在适用性方面受到较大影响。基于Lamb波的时间反转聚焦原理,考虑损伤定位过程中的不确定性因素,发展了一种基于Bayesian理论的无参考信号主动Lamb波损伤定位方法。根据时反聚焦信号中主、旁瓣波包峰值的相对时刻,提取各测量通道损伤散射信号传播时间与直达波传播的时间之差作为样本,并基于Bayesian理论,获得损伤位置、波速等未知参数的联合后验概率分布,再利用马尔科夫链蒙特卡洛(MCMC)方法在后验分布中对未知参数进行采样估计,得到马尔科夫链的极限分布即未知参数的后验分布。通过对一铝质矩形薄板的数值仿真和模型实验研究结果表明,该方法能够较为准确地识别出损伤位置、波传播速度及其不确定性。
关键词:主动Lamb波;损伤定位;时间反转;Bayesian理论;MCMC方法
中图分类号:0347.4
文献标志码:A
文章编号:1004-4523(2017)01-0033-08
DOI:10.16385/j.cnki.issn.1004-4523.2017.01.005
引言
作为超声无损检测中最常见的一种导波形式,Lainb波具有沿传播路径衰减小、传播距离远等特点,并对结构的微小损伤敏感,对板状结构大面积无损检测具有很大优势。现有的主动Lamb波损伤监测方法大多基于参考信号,即以健康状态响应信号为基准,通过对信号作差的方法获取损伤散射信号,但真实结构和外界环境的变化对其影响很大,使其在适用性方面受到较大影响。此外,传统的基于损伤散射信号传播时间的损伤定位方法,如,脉冲回波法、椭圆定位法、四点圆弧定位法等,均把损伤散射信号传播时间与一定频厚积下的波速等控制参数视为确定性值,而事实上,实际应用中测量误差、模型误差等导致的损伤定位结果的不确定性不可避免。如,损伤识别前,损伤尺寸、损伤程度及材料特性通常无法获知,且损伤、材料的非均值性及各向异性等对波速产生的影响也不明确,这将反过来影响通过理论计算所得到的损伤散射信号传播时问。再者,用以作激励与传感的压电片尺寸效应也未考虑,这都给损伤的准确定位带来影响。除此之外,由于Lamb波的频散特性,损伤散射信号波包在传播过程中会发生畸变,也会对损伤散射信号传播时问的确定产生影响。因此,在Lamb波损伤定位中有必要考虑不确定性因素对损伤定位结果的影响,开展基于不确定性方法的主动Lamb波损伤诊断研究。
本文首先根据板状结构中主动Lamb波时间反转理论,分析了单损伤板结构中单模式Lamb波时间反转聚焦过程以及Lamb波无基准损伤散射信号传播时间与直达波传播时间之差提取原理。考虑损伤识别过程中模型本身及测量等存在的不确定性与误差,将基于时间反转原理获取的传感器列阵中各监测路径的损伤散射信号传播时间与直达波传播时问之差作为损伤位置、波速等未知参数的样本,再结合未知参数的先验信息,基于Bayesian理论,得到未知参数的联合后验概率分布。最后通过McMc方法在联合后验概率分布中对未知参数进行采样,得到各未知参数的后验概率密度分布,实现板状结构不确定性损伤定位。
1.理论背景
1.1单损伤板结构中Lamb波的时反聚焦
近年来,从光学领域的相位共轭法引伸而来的Lamb波时间反转处理方法逐渐引起学者们的广泛关注。Lamb波的时反指将传感器所接收到的各模式信号在时间域上反转后,再在传感器上加载,即所接收信号先到后发、后到先发,从而实现各模式信号在原始激励处的自适应聚焦与频散补偿。为降低信号处理的复杂程度,选择合适中心频率的窄带信号以尽量激发出单模式为主的Lamb波信号。
1.3 MCMC数值模拟方法
由Bayesian理论给出的单个未知参数后验概率分布(即公式(11))的计算需要求解高维多重数值积分,而常规的Monte Carlo模拟方法计算量过大,此类问题较方便采用MCMC模拟方法进行处理。MCMC方法是以动态构造Markov链为基础,通过遍历性约束来实现模拟目标分布的一类随机模拟方法,它能把一些复杂的高维问题转化为一系列简单的低维问题,为复杂统计模型的多参数高维数值积分计算问题提供一种有效工具。通过合理的定义与实施,MCMC方法总能得到一条具有平稳分布的马尔科夫链,该马尔科夫链的平稳分布即为目标后验分布。
采用双面激励方式产生单-A。模式Lamb波信号进行检测,在本算例选取的频厚积数值下,该模式波包的群速度相比s。模式小很多,且本例损伤散射信号与直达波传播路径均相距较小,若以s。模式进行损伤定位,传感信号在时间域上将表现为直达波信号与损伤散射信号波包到达时刻很接近,引起损伤散射信号与直达波信号的混叠,给后续信号分析处理带来较大困难,因而本文取Ao模式Lamb波进行损伤识别。依次选取各压电元件為激励器,其余压电元件作为传感器,根据声波互易性原理,在所有可能激励一接收路径信号组合中有6个是独立的,分别表示为f12,f13,f14,f23,f24和f34其中下标数字分别表示激励器与传感器的编号。对采集到的各监测路径响应信号施加合适的窗函数进行截取,消除边界反射信号,仅保留直达波信号和损伤散射信号,并将截取后的信号在时域上进行反转处理后再次用作激励,得到结构的时反聚焦信号,最后提取各监测路径上时反重构信号主、旁瓣时间差值用于本文方法的损伤定位。
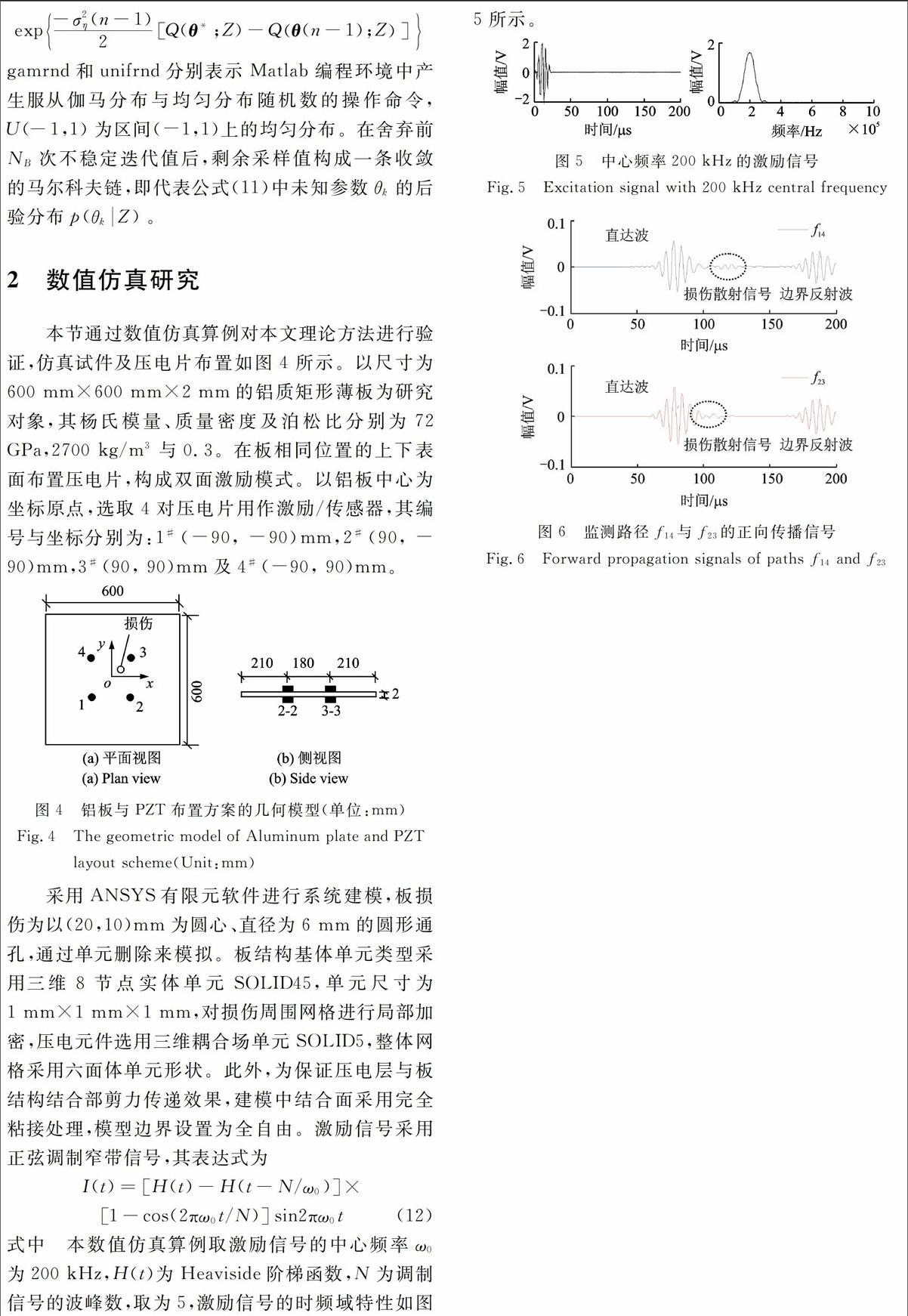
以f14与f23测量路径为例介绍,ANSYS仿真得到的板结构对应响应信号如图6所示,对各路径信号进行截取,仅保留直达波和损伤散射信号,并对截取后的信号在时域内进行反转处理以再次作为激励,如图7所示。图8为获得的时反聚焦响应信号,对比图6可以看出,由于路径f14损伤散射波包较为独立,时反加载处理后仍然较清晰。其中,主瓣左右两侧对称出现的旁瓣信号为分别为缺陷散射信号产生的直达波信号以及原始直达波信号所产生的损伤散射信号。从图6中还可看出,路径f23的损伤散射信号与直达波信号部分混叠,但经时反操作后,重构信号中损伤旁瓣信号变得较为明显(见图8),表明本文方法中的时反操作能在一定程度上补偿Lamb波频散效应,便于时间差提取,较传统非时反方法的时间差提取具有一定优势。
根据公式(3)所表述的时反聚焦信号中主、旁瓣信号对应波峰的相对时间关系,在生成时反信号包络图(见图8)基础上提取各监测路径下Lamb波损伤散射信号与直达波信号传播时问之差,如表1所示。应指出,对于监测路径f13和f24,由于损伤距离直达波路径很近、信号散射角度大,加之Lamb波的频散效应导致的波包延拓与幅值衰减,损伤散射信号完全混叠在直达波信号中,导致时反重构信号中不会出现旁瓣信号,因而得不到相应路径上的损伤散射信号与直达波信号的传播时间差,故其结果未列于表1。
图9表示通过本文MCMC方法采样所得的损伤坐标位置以及激励中心频率为200kHz时的波传播速度,其中,假定坐标参数z和y的先验分布服从[-90,90]mm内的均匀分布,且波速也同样服从[0,3000]m/s内的均匀分布。从该图中可以看出,经过较少迭代次数后,各采样值均趋于稳定,并在偏离该值附近的小范围内波动。MCMC算法采样的个数取为NT=6×104,将收敛前的NB=1×104次不稳定迭代值舍去,利用参数x,y剩余的5×104个样本值识别得到损伤中心坐标为(20.7,10.5)mm,与实际损伤中心位置(20,10)mm很接近。同时,从图9中还可看出波速识别结果与给定频厚积下频散曲线理论结果也吻合较好。
图10为损伤位置坐标的联合概率分布,从该图中可以看出,损伤位置坐标值的联合概率密度函数在xy平面投影分布于一个较小范围,且概率值沿峰值各方向均下降很快,表明所识别出的损伤位置坐标值不确定性程度较小。
3.实验研究
开展实验研究以对本文方法进一步验证,实验系统布设如图11所示,其中,主要实验设备包括:数据采集器(NI PXLe-1071)、接线盒(NI NBC-2102)、安装LabVIEW的PC机、PZT-5圆形压电陶瓷片(无锡海鹰公司生产,直径8mm、厚度0.48mm),实验对象为800mm×800mm×2mm铝质薄板,损伤形式为圆形通孔,中心位置(-50,-50)mm、直径10mm。选用4个压电片构成激励一传感列阵,并采用中心频率为100kHz的5波峰正弦调制信号激励,产生的Lamb波以A。模式为主,响应信号的采样频率取为2MHz。
以监测路径fAB。的响应信号为例,图12给出该路径的正向传播信号与时反聚焦信号。可以看出,损伤散射信号部分混叠在直达波信号中,经时反处理后,重构信号的主瓣两侧出现较明显的旁瓣信号,与此前数值仿真现象类似,再次表明本文时反方法对Lamb波频散效应的补偿特性。
利用时反信号中主、旁瓣信号波包值峰时刻的相对关系,提取各监测路径下Lamb波损伤散射信号与直达波传播的时间差,结果列于表2,其中,由于监测路径fAC,fBD。(此处的A,B,c,D即图11中的PZTA,PZTB,PZTC和PZTD所处位置)上损伤距离直达波路径很近而导致损伤散射信号完全混叠于直达波信号中,无法提取时间差,故未列出相关结果。同时,该表中斜线后数字表示通过ANSYS仿真计算得到的时间差结果,可以看出其与实验结果较符合。
图13表示实验条件下本文MCMC方法采样所得的损伤中心坐标及激励中心频率为100kHz时波传播速度,其中,采样点总数为1x105,且假定损伤中心坐标与波速的先验分布分别服从[-150,150]mm与[0,3000]m/s范围内的均匀分布。从该图中可以看出,经历较少次数的波动后,分别获得关于损伤位置参数与波速的稳定马尔科夫链。
为验证实验损伤位置识别结果,舍弃收敛前的NB次不稳定迭代样本,图14分别给出实验及AN-SYS仿真条件下损伤识别位置与实际损伤位置范围,对比结果可以明显看出,实验与仿真结果均接近于实际损伤中心位置,且实验损伤识别位置的离散程度较仿真结果大。其中,实验与仿真条件下MC-MC样本统计得到的损伤识别位置平均值分别为(-51.1/-50.7,-51.4/-50.9)mm,標准差分别为(3.8/1.3,3.2/1.7)mm,且该定量对比结果与图14给出的定性观察结果吻合较好。
此外,图15给出实验条件下得到的损伤中心坐标值的联合概率密度分布,该概率密度最大值集中在实际损伤中心位置附近,与图14结果较吻合,其进一步验证了本文提出的损伤概率定位方法的正确性。
4.结论
本文提出了一种基于Bayesian理论的板状结构主动Lamb波损伤定位方法,该方法利用时间反转理论消除对结构健康状态下参考信号的依赖。数值仿真和实验研究结果均表明,本文方法可以不依赖健康状态基准信号,而直接通过对当前状态下结构各监测路径的响应信号进行提取并分析,以实现损伤定位。同时,Bayesian理论结合MCMC采样方法能合理地考虑损伤识别过程中模型误差与测量噪声等因素所引起的不确定性,损伤定位结果更加可靠。此外,本文方法中时间反转变换能在一定程度上补偿Lamb波频散效应,有利于时间差的准确提取,较传统非时反方法的时间差提取具有一定优势。在实际应用中,考虑到结构本身、Lamb波频散及外界环境变化等诸多不确定性因素引起的健康状态基础信号与损伤定位结果的不确定,本文方法仅依赖结构当前状态测量信号检测损伤,对于板状结构大面积无损检测与健康状态的长期实时监测,具有一定的理论与实际意义。
