随机交通网络最小期望-均方差路径问题罚函数解法*
2017-04-20潘义勇马健霄
潘义勇,马健霄
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
随机交通网络最小期望-均方差路径问题罚函数解法*
潘义勇,马健霄
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
为了反映交通网络中考虑可靠性的路径选择行为,基于数学规划理论建立随机交通网络环境下最优路径问题的数学模型并构造罚函数法求解该约束优化问题。首先,在路径目标函数中加入了均方差以反映路径的可靠性,建立随机网络环境下最小期望-均方差路径问题的数学规划模型;其次,引入罚函数和罚因子,把非线性约束优化问题转换为无约束优化问题;第三,构造拟牛顿法求解无约束优化问题,最终获得原问题的精确解;最后,针对实际交通网络开展了数值实验并对数值结果进行了分析。数值结果表明:提出的算法是能获得最优路径的精确解。
交通运输工程;随机网络;最优路径;罚函数;拟牛顿法
0 引 言
交通网络最优路径问题是车辆导航系统的核心问题[1]。交通网络最优路径问题的建模有两个关键环节,首先是建立能够准确反映交通网络耗时随机特性的网络模型,通过数据采集获取并拟合网络模型参数,实现网络模型的数值化计算;其次是在交通网络模型基础上建立最优路径模型,选择合理的路径目标函数准确反映实际交通网络路径选择行为。其中,前者发展已经很成熟,随机网络[2]指网络的边的权值是服从一定概率分布函数的随机变量,反映交通网络行程时间的随机特性。后者根据路径目标函数所反映的路径选择行为主要分为最小期望路径问题[2]和最可靠路径问题[3-8]。最小期望路径问题的目标是寻找起讫点之间的获得最小期望值的路径。最小期望路径问题能反映考虑行程时间随机性的路径选择行为,不能反映考虑可靠性的路径选择行为,对于风险规避的行驶者不仅关注行程时间的节省而且关注行程时间的可靠性。最可靠路径问题针对考虑可靠性的路径选择行为,为了反映这一点,各种可靠性指标加入到路径目标函数中[3-8],直接的和间接的反映路径行程时间的可靠性。其中以行程时间期望值与均方差之和最小为路径目标函数最能直接反映风险规避的行驶者对路径的可靠性的需求,称为随机网络最小期望-均方差路径问题[6]。
1983年R.W.HALL[5]注意到行驶者常常预留部分时间以应对出行时间的随机性,行程时间的均值和预留时间之和称为有效的行程时间。有效的行程时间实际上是随机行程时间的期望值和均方差的线性组合,反映了该路径随机行程时间的可靠性,并以有效的行程时间为路径目标函数定义了随机网络最可靠路径问题。同时利用枚举法求解随机网络环境下最可靠度路径问题,但是该算法只是理论上的算法,不能应用于实际网络。2001年S.SEN等[6]以期望值和方差之和为路径目标函数,建立了最小期望-方差路径问题模型,并且利用松弛算法求解了其近似解的集合。但是方差和期望值不在一个量纲上,不能直接反映路径可靠性。相比较而言,研究的随机网络最小期望-均方差路径问题就能克服这个问题。同时,由于均方差的不可加性和非线性,所以最小期望-均方差路径问题的求解比最小期望-方差路径问题要复杂。2011年T.XING等[7]讨论了在随机网络环境下最小期望-均方差路径问题,构造了拉格朗日松弛算法求解了该问题的解的下界,没有获得该问题的精确解。2013年B.Y.CHEN等[8]基于随机优势理论研究了寻找最小有效行程时间的路径问题,考虑了随机变量的相关性[9],并把该问题推广到了动态随机网络[10],但是均假设路径的行程时间是满足正态分布的随机变量,具有局限性;2015年A.KHANI等[11]给出了最小期望-方差路径问题和最小期望-均方差路径问题解之间的关系,并求解了最小期望-均方差路径问题的上界。
综上所述,针对随机交通网络最小期望-均方差路径问题的建模已经非常完善。由于该问题目标函数的不可加性和非线性,不能通过基于动态规划的算法求解该问题。现有研究都是把该问题松弛为动态规划问题求的原问题的近似解,没有给出原问题的精确解,而这正是本研究的目的。为了反映交通网络中考虑可靠性的路径选择行为,基于数学规划理论建立随机交通网络环境下最优路径问题数学模型并构造罚函数法求解该约束优化问题。首先,在路径目标函数中加入了均方差以反映路径的可靠性,建立随机网络环境下最小期望-均方差路径问题的数学规划模型;其次,引入罚函数和罚因子,把非线性约束优化问题转换为无约束优化问题;第三,构造拟牛顿法求解无约束优化问题,最终获得原问题的精确解;最后,针对实际交通网络开展了数值实验并对数值结果进行了分析。
1 问题描述与建模
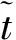
如果利用二进制来表示先验路径x∈Kod,可得
x={xij∈{0,1}|(i,j)∈A}
(1)
其中xij=1表示边(i,j)在先验路径x上,xij=0表示边(i,j)不在先验路径x上。此时先验路径x上的行程时间为
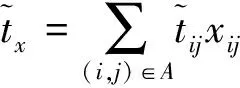
(2)
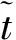
(3)
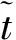
(4)
根据不同的可靠性指标,随机网络环境下最可靠路径的定义也是不一样的,其中以行程时间期望值与均方差之和最小为路径目标函数最能直接反映风险规避的行驶者对路径的可靠性的需求,笔者定义路径的目标函数为期望值与均方差线性之和:
(5)
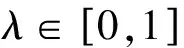

(6)
采用的期望值-均方差路径目标函数为非线性函数,不具有可加性,这就增加了求解该问题的难度,相对来说,随机网络环境下最小期望-方差路径问题由于其目标函数的线性和可加性,求解相对比较容易。下面我们构造罚函数法求解上述混合非线性整数约束优化问题(6)的精确解。
2 求解算法
本节设计基于罚函数的拟牛顿法求解随机网络环境下最小期望-均方差路径问题,首先构造罚函数[12]把混合非线性整数约束优化问题(6)转化为非线性无约束优化问题,再设计拟牛顿法求解该非线性无约束优化问题。
2.1 罚函数
罚函数法[12]是通过求解一个或多个罚函数的极小来求解约束优化问题的方法,罚函数法的基本思想就是通过罚函数把约束优化问题转换为无约束优化问题,再对无约束优化问题进行求解,其中罚函数的构造在该方法中起着关键作用。下面我们构造问题(6)的罚函数。
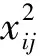
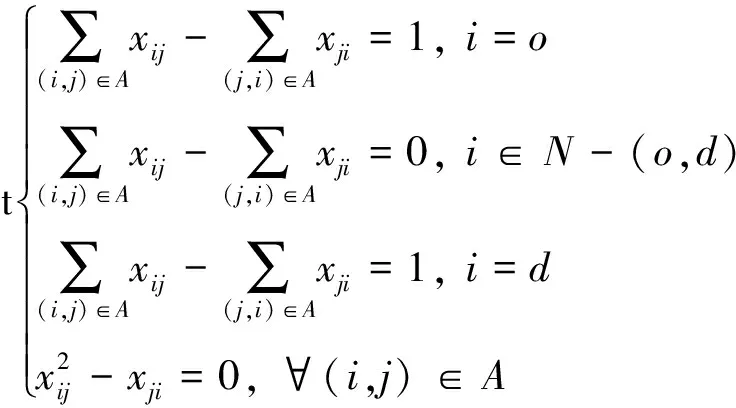
(7)
下面我们要把上述问题转换为无约束优化问题。最优化理论中常用方法为罚函数法,通过罚函数把优化问题中的约束条件转化为目标函数,当约束条件满足时目标函数最小。针对上述问题(7)定义罚函数:
(8)
因此通过罚函数可以把问题(7)转换为无约束优化问题(9):
minf(x)+γ×g(x)
(9)
其中γ=1/ε≥0为罚因子,当ε→0时,无约束优化问题的最优解就是原问题的最优解。
2.2 拟牛顿法
本节设计基于迭代算法的拟牛顿法求解无约束优化问题(9),拟牛顿法是求解非线性无约束优化问题最有效的方法之一[12]。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化,构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法,尤其对于大规模的问题。另外,因为拟牛顿法不需要二阶导数的信息,所以有时比牛顿法更为有效。如今,优化软件中包含了大量的拟牛顿算法用来解决无约束,约束,和大规模的优化问题。
为了求解无约束优化问题(9),拟牛顿法的基本思想是每次迭代xk,使得其趋向于最优值点x*,f(xk)+γ×g(xk)随着k的增大而更接近最优值f(x*)+γ×g(x*),并且近似误差随着k的增大而减小, 其每次迭代的公式为
xk+1=xk+akpk,
(10)
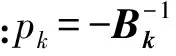
(11)
其中:sk=xk+1-xk,yk=▽[f(xk+1)+γ×g(xk+1)]-▽[f(xk)+γ×g(xk)];当k=0时,Bk取单位矩阵。
ak为满足以下Wolfe条件[8]的迭代步长:
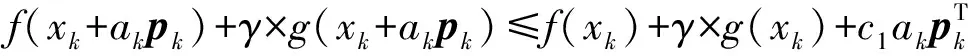
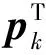
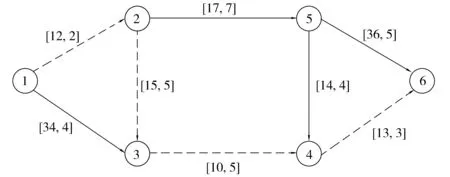
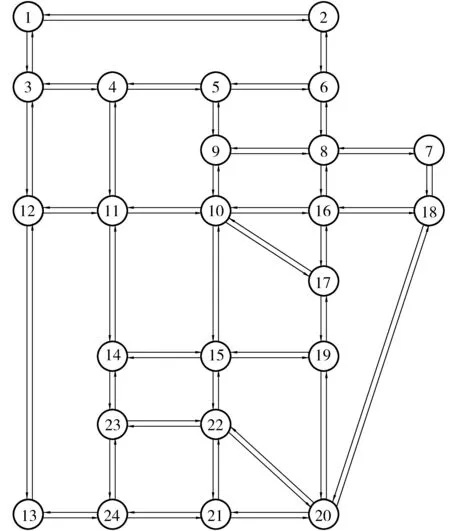
其中:0 表1 算法1 3.1 小网络 图1 随机网络Fig. 1 Stochastic network 该随机网络环境下最小期望-均方差路径问题建模为下列混合非线性整数约束优化问题: minf(x) (12) 其中 (13) 通过构造罚函数 (14) 上述混合非线性整数约束优化问题转化为下列无约束优化问题: minf(x)+γ×g(x) (15) 其中罚因子γ=1×107。 通过MATLAB计算机语言编写拟牛顿算法Algorithm 1求解上述无约束优化问题,并且在Windows-10 (64) 工作站(two 2.00 GHz Xeon CPUs and 4G RAM)条件下运行的,计算获得的最优值点和最优值分别为 x=(x12,x13,x23,x25,x34,x46,x54,x56)=(1.0,-0.0,1.0,-0.0,1.0,1.0,0.0,-0.0) 相应的最小期望-均方差路径为1→2→3→4→6,该路径的期望值与均方差线性和为54.549 1,具体路径如图2。 图2 最小期望-均方差路径Fig. 2 Mean-standard deviation shortest path 3.2SiouxFallsnetwork 通过MATLAB计算机语言编写拟牛顿算法Algorithm 1求解上述无约束优化问题,并且在Windows-10 (64) 工作站(two 2.00 GHz Xeon CPUs and 4G RAM)条件下运行的,求得的最优路径如图4中虚线所示。 图3 苏福尔斯网络Fig. 3 Sioux Falls network 图4 最小期望-均方差路径Fig. 4 Mean-standard deviation shortest path 从以上的计算结果可以得出以下结论: 第一,笔者提出的罚函数法能够求解随机网络环境下最小期望-均方差路径问题的精确解,获得确定最优路径和最优解,能直接反馈给驾驶员最优路径和行程时间。相比较而言,已有的算法求解都是近似解,获得的是最优路径的集合和最优解的上下界,并且最优路径的集合规模会随着问题规模增大而增大,限制了其在实际路径导航中的应用。 第二,通过罚函数把随机网络环境下最小期望-均方差路径问题转化为无约束优化问题。当罚因子γ得取值足够大时,无约束优化问题的最优解等于原问题的解,两个问题是等价关系。另一方面,无约束优化问题的求解方法已经很成熟了,对于大规模问题都有很好的计算效率。所以笔者提出了求解最小期望-均方差路径问题很好的一个思路。 第三,通过罚函数把随机网络环境下最小期望-均方差路径问题转化为无约束优化问题。其中无约束优化问题的求解算法已经研究得很成熟,在优化软件中采用较多,这有利于我们进一步利用现有软件实现最可靠路径的导航应用研究。 针对交通网络的随机特性以及考虑可靠性的路径选择行为,基于混合整数规划建立随机网络环境下最小期望-均方差路径问题的数学模型。通过构造罚函数把上述问题转化为无约束优化问题,构造了基于拟牛顿法的迭代算法求解该无约束优化问题。通过对交通网络的计算验证了该算法的正确性和可行性。该算法的提出为随机交通网络最小期望-均方差路径问题的解决从数学规划的角度提供了一个好的思路和有效的工具。本研究仅考虑了交通网络行程时间的随机特性,没有考虑其动态特性,因此把笔者提出的模型推广到动态随机网络是需要继续研究的课题。 [1] FARAHANI R Z, MIANDOABCHI E, SZETO W Y, et al. A review of urban transportation network design problems[J].EuropeanJournalofOperationalResearch, 2013, 229(2):281-302. [2] GAO S, CHABINI I. Optimal routing policy problems in stochastic time-dependent networks[J].TransportationResearchPartB:Methodological, 2006, 40(2):93-122. [3] 潘义勇, 孙璐. 随机交通网络环境下自适应最可靠路径问题[J]. 吉林大学学报(工学版), 2014,44(6):1622-1627. PAN Yiyong ,SUN Lu. Adaptive reliable shortest path problem in stochastic traffic network[J].JournalofJilinUniversity(EngineeringandTechnologyEdition), 2014,44(6):1622-1627. [4] 潘义勇, 马健霄, 孙璐. 基于可靠度的动态随机交通网络耗时最优路径[J]. 吉林大学学报 (工学版), 2016,46(2):412-417. PAN Yiyong,MA Jianxiao, SUN Lu. Optimal path in dynamic network with random link travel times based on reliability[J].JournalofJilinUniversity(EngineeringandTechnologyEdition), 2016,46(2):412-417. [5] HALL R W. The fastest path through a network with random time-dependent travel times[J].TransportationScience, 1986, 20(3):182-188. [6] SEN S, PILLAI R, JOSHI S, et al. A mean-variance model for route guidance in advanced traveler information systems[J].TransportationScience, 2001, 35(1):37-49. [7] XING T, ZHOU X. Finding the most reliable path with and without link travel time correlation:a lagrangian substitution based approach[J].TransportationResearchPartB:Methodological, 2011, 45(10):1660-1679. [8] CHEN B Y, LAM W H K, SUMALEE A, et al. Finding reliable shortest paths in road networks under uncertainty[J].NetworksandSpatialEconomics, 2013, 13(2):123-148. [9] CHEN B Y, LAM W H K, SUMALEE A, et al. Reliable shortest path finding in stochastic networks with spatial correlated link travel times[J].InternationalJournalofGeographicalInformationScience, 2012, 26(2):365-386. [10] CHEN B Y, LAM W H K, SUMALEE A, et al. Reliable shortest path problems in stochastic time-dependent networks[J].JournalofIntelligentTransportationSystems, 2014, 18(2):177-189. [11] KHANI A, BOYLES S D. An exact algorithm for the mean-standard deviation shortest path problem[J].TransportationResearchPartB:Methodological, 2015, 81:252-266. [12] 袁亚湘. 非线性优化计算方法[M]. 北京:科学出版社, 2008. YUAN Yaxiang.NonlinearOptimizationMethod[M]. Beijing:Science Press, 2008. (责任编辑:朱汉容) Penalty Function Algorithm for Solving the Mean-Standard Deviation Shortest Path Problem in Stochastic Traffic Network PAN Yiyong,MA Jianxiao (College of Automobile and Traffic Engineering, Nanjing Forestry University, Nanjing 210037, Jiangsu, P. R. China) In order to reflect route choice behavior considering the reliability in traffic network, a mathematic model of shortest path problem in stochastic network was developed based on the mathematical programming and a penalty function algorithm was constructed to solve the constrained optimization problem. Firstly, a mathematical model of mathematical programming was established to reflect the reliable shortest path selection in stochastic network through defining the standard deviation as the part of the objective function; Secondly, the nonlinear constrained optimization problem was transformed into unconstrained optimization problem through introduction of penalty function and penalty factor; Thirdly, a quasi-Newton method is developed to solve the proposed problem; Finally, numerical experiments was carried out on the actual traffic network and the numerical results were analyzed. Numerical results show that the proposed algorithm is able to get exact solution of the optimal path. traffic and transportation engineering; stochastic network; optimal path; penalty function; quasi-Newton method 10.3969/j.issn.1674-0696.2017.04.17 2016-03-15; 2016-05-18 国家自然科学基金青年基金项目(51508280);南京林业大学高学历人才基金项目(GXL2014031);江苏省高等学校大学生创新创业训练计划项目(201610298037Z) 潘义勇(1980—),男,安徽安庆人,博士,主要从事交通网络研究方面的研究。E-mail:uoupanyg@163.com。 U491 A 1674-0696(2017)04-096-06
3 数值试验



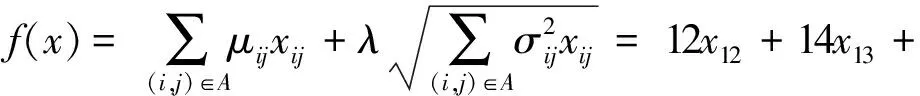

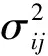

4 结 语
