巧用矩形对角线
2017-04-20顾啸敏
顾啸敏
巧用矩形对角线
顾啸敏

平行四边形是近几年各地中考考查的重点知识,而矩形又是特殊的平行四边形,对角线相等是矩形的重要性质之一,如果能巧妙地利用这个性质,可以使某些问题得到简单而快捷的解决.
一、计算求值
例1如图1,在▱ABCD中,对角线AC、BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同速度向C、A运动.
(1)四边形DEBF是平行四边形吗?并说明理由.
(2)若BD=10cm,AC=16cm,当运动时间t为多少时,四边形DEBF为矩形.
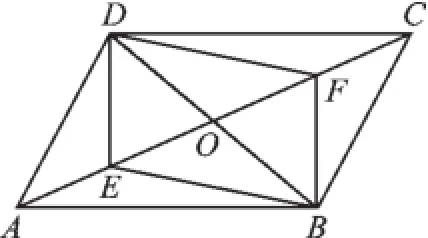
图1
【分析】(1)判定平行四边形的方法有很多种,可通过证明△ADE≌△CBF、△ABE≌△CDF,利用两组对边分别相等或者一组对边平行且相等来证明,这里利用对角线互相平分来判定平行四边形最为简捷.
(2)▱DEBF在运动过程中要成为矩形,只需满足对角线相等即可.这里还要注意E、F两个动点运动的位置可能在点O的上方,也有可能在点O的下方,不能遗漏.
解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E、F是两动点,运动的速度相同,
∴AE=CF,
∴OA-AE=OC-FC,
即:OE=OF,
∴四边形DEBF是平行四边形.
(2)当DB=EF时,四边形DEBF为矩形.
当点E在点O的下方时,
10=16-2t,t=3;
当点E在点O的上方时,
10=2t-16,t=13.
∴当t=3s或13s时,四边形DEBF为矩形.
二、证明相等
例2如图2,在正方形ABCD中,E是对角线AC上的一点,EF⊥CD于点F,EG⊥AD于点G.求证:BE=FG.

图2
【分析】通过观察,线段BE与FG所在的三角形不可能全等,它们也不在同一个四边形中,不能利用特殊四边形的性质,所以直接证明它们相等非常困难.但如果构造矩形的对角线,利用对角线相等的性质进行转化,问题就可以迎刃而解了.

三、推导定理
例3已知在Rt△ABC中,∠ABC=90°,点O是AC的中点,求证:OB=AC.
【分析】证明线段的倍分关系通常转化为证明两条线段的相等,加倍延长BO到D,可以证明四边形ABCD是矩形,从而利用矩形的性质得到结论.
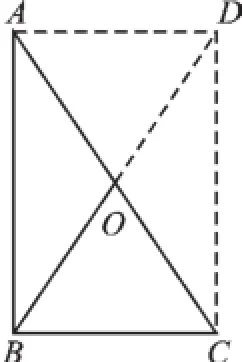
图3
证明:如图3,延长BO到D,使OD=OB,连接AD、CD.
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴▱ABCD是矩形,∴BD=AC,2OB=AC,
例3的结论用文字语言描述为:“直角三角形斜边上的中线等于斜边的一半”,这个定理在几何计算和证明中的应用非常广泛.
四、探求最值
例4如图4,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形,求线段DE长度的最小值.
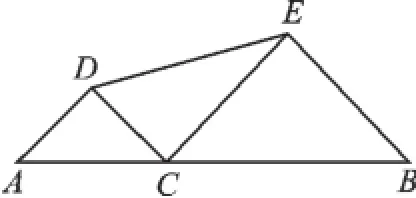
图4
【分析】当点C在线段AB上运动时,点D、E随之运动,线段DE长度也随之变化,但等腰直角三角形的形状没有改变,∠A、∠B的度数一直是45°,假设延长AD、BE交于点G,则△ABG也是等腰直角三角形,四边形DCEG是矩形,根据矩形对角线相等的性质,线段DE转化为GC,从而利用“垂线段最短”的性质巧妙地解决问题.

图5
解:如图5,延长AD、BE交于点G,连接CG,则△ABG为等腰直角三角形,四边形DCEG为矩形,∴DE=GC.
∴线段DE长度的最小值为1.
此解法通过添加适当的辅助线,巧妙地构造矩形,利用矩形对角线相等的性质将DE转化为GC,利用“垂线段最短”直接求解,避免了复杂的代数运算,较为简捷.
江苏省宝应县实验初级中学)
