“特殊的平行四边形”易错点剖析
2017-04-20徐永军
徐永军
“特殊的平行四边形”易错点剖析
徐永军
特殊的平行四边形作为平行四边形的一部分,在历年中考中也占有非常重要的地位,但是本块内容概念多,性质定理和判定方法多样化,同学们容易混淆犯错,所以下面就一些常见的错误举例并加以分析.
一、不能正确理解特殊的平行四边形的概念和识别方法
例1给出下列结论:
①有一组对边平行,且两个角是直角的四边形是矩形;②两条对角线相等的四边形是矩形;③两组对边分别相等的四边形是矩形;④有一个角是60°的平行四边形是菱形;⑤有两边相等的平行四边形是菱形;⑥有一组邻边相等的矩形是正方形;⑦有三边相等,且有一个角是直角的四边形是正方形;⑧对角线相等且互相垂直平分的四边形是正方形.其中正确的有().
A.2个B.3个C.4个D.5个
【错解】B或C.
【正解】A.
【错解辨析】解决本题的关键是正确理解各种特殊的平行四边形的概念和识别方法.①是错误的.如图1-1所示,∠A=∠B=90°,AD∥BC,由图形可知完全符合条件,但它不是矩形.②是错误的.对角线相等的平行四边形是矩形,对角线相等的四边形不一定是平行四边形,因此,只有当对角线相等且互相平分时,这个四边形才是矩形.③是错误的.两组对边分别相等的四边形是平行四边形,而矩形是特殊的平行四边形,即有一个角是直角的平行四边形.④是错误的.有一个角是60°的平行四边形不能保证邻边相等.⑤是错误的.只有邻边相等的平行四边形才是菱形.⑥是正确的.⑦是错误的.如图1-2所示,AB=AD=BC,∠B=90°,由图形可知四边形ABCD并不是正方形.⑧是正确的.
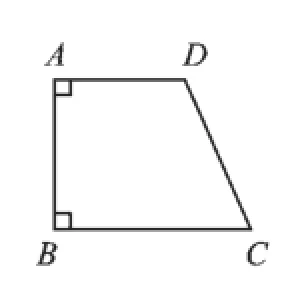
图1-1

图1-2
二、在证明过程中忽视条件
例2如图2,在平行四边形ABCD中,AC和BD交于点O,OE⊥AD于E,OF⊥BC于F,OE=OF.为什么?
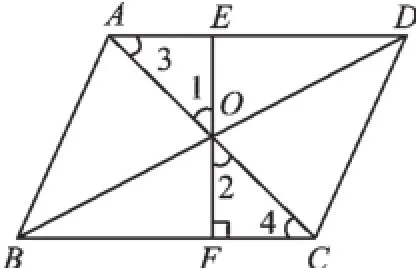
图2
【错解】∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.∵AD∥BC,∴∠3=∠4.
∵∠1=∠2,∴△AOE≌△COF(ASA).
∴OE=OF.
【正解】证法1:∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC.
∵AD∥BC,∴∠3=∠4.
∵OE⊥AD于E,OF⊥BC于F,
∴∠AEO=∠CFO=90°.
∴△AOE≌△COF(AAS).∴OE=OF.
证法2:∵四边形ABCD是平行四边形,
∴AD∥BC.∵OE⊥AD,∴OE⊥BC.
又OF⊥BC,∴直线OE与OF重合,即E、O、F三点共线,∴∠1=∠2.
又∵OA=OC,∠AEO=∠CFO=90°,
∴△AOE≌△COF(AAS).∴OE=OF.
【错解辨析】本题容易出现的错误是直接使用∠1=∠2证明△AOE≌△COF,这样就默认了E、O、F三点共线,而已知条件中并没有这个结论,因此E、O、F三点共线在证明过程中必须加以说明,否则就是错误的.
三、混淆特殊平行四边形的对称性
例3下列所述图形中,是中心对称图形,但不是轴对称图形的是().
A.矩形B.平行四边形
C.菱形D.正方形
【错解】A、C或D.
【正解】B.
【错解辨析】错解的原因是混淆特殊平行四边形的对称性.平行四边形是中心对称图形,其对称中心是对角线交点,因为矩形、菱形、正方形都是特殊的平行四边形,所以它们都是中心对称图形.很多同学误以为平行四边形也是轴对称图形,对角线所在直线是其对称轴,其实只要亲自操作一次就不难发现平行四边形并不是轴对称图形,而矩形、菱形、正方形都是轴对称图形,其中矩形、菱形有两条对称轴,正方形有四条对称轴.
四、不能准确识别中点四边形形状
例4顺次连接对角线互相垂直的四边形的各边中点所得四边形一定是().
A.矩形B.平行四边形
C.菱形D.正方形
【错解】B、C或D.
【正解】A.
【错解辨析】许多同学搞不清楚中点四边形如何判定,其实识别方法并不难,总结规律如下:①顺次连接四边形各边中点所得四边形是平行四边形;②顺次连接对角线相等的四边形各边中点所得四边形是菱形;③顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形;④顺次连接矩形各边中点所得的四边形是菱形;⑤顺次连接菱形各边中点所得的四边形是矩形;⑥顺次连接正方形各边中点所得的四边形是正方形.由以上规律,我们还可以得出一般性结论:①当原四边形对角线相等时,顺次连接四边中点所得四边形是菱形;②当原四边形对角线互相垂直时,顺次连接四边中点所得四边形是矩形;③当原四边形对角线既相等又垂直,则顺次连接四边中点所得四边形既是菱形又是矩形,也就是正方形.
五、问题考虑不够全面
例5长为30,宽为a的矩形纸片(15<a<30),如图3-1那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图3-2那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n次操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为______.
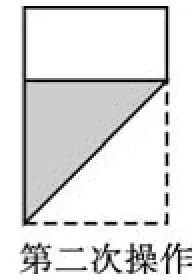
图3-2
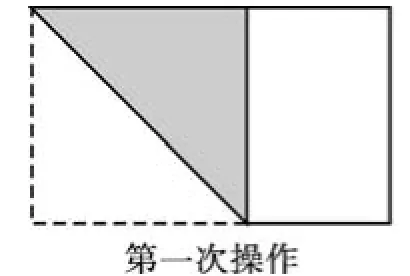
图3-1
【错解】18.
【正解】18或22.5.
【错解辨析】根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽.当15<a<30时,矩形的长为30,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为30-a,a.由30-a<a可知,第二次操作时所得正方形的边长为30-a,剩下的矩形相邻的两边分别为30-a,a-(30-a)=2a-30.由于(30-a)-(2a-30)= 60-3a,所以(30-a)与(2a-30)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①30-a>2a-30;②30-a<2a-30.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
江苏省宝应县实验初级中学)
