融合数学之本,运筹帷幄之中
2017-04-20徐菊萍
融合数学之本,运筹帷幄之中
徐菊萍

“三角形”是初中数学“空间与图形”中最基本也是最核心的内容.知识点非常多,考查形式也多样化,既可独立成题,又常融入四边形、圆、函数等知识,以综合题的形式出现.要对三角形的知识融会贯通,我们可以从以下五个方面来串联.
一、三角形内部的知识
例1(2016·黄石)如图1所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=().

图1
A.50°B.100°C.120°D.130°
【解析】已知线段AC的垂直平分线交线段AB于点D,根据线段垂直平分线的性质可得AD=DC,由等腰三角形的性质可得∠A=∠DCA= 50°,进而根据三角形外角的性质可得∠BDC=∠A+∠DCA=100°,故答案选B.
【点评】本题考查线段垂直平分线的性质、三角形外角的性质.不少同学通过内角和先求∠ADC=80°,再用邻补角求∠BDC,虽然也能求出答案,但不是捷径,要寻求最佳途径,需熟练掌握相关性质,并能灵活运用.
例2(2016·广州)如图2,已知△ABC,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于D,连接CD,CD=().

图2
A.3B.4C.4.8D.5
【解析】已知AB=10,AC=8,BC=6,根据勾股定理的逆定理可判定△ABC为直角三角形,又因DE为AC边的中垂线,可得DE⊥AC,AE= CE=4,所以DE为△ABC的中位线,即可得DE为BC的一半,值为3,再根据勾股定理求出CD=5,故答案选D.
【点评】本题主要考查勾股定理及其逆定理、中位线定理、中垂线的性质.要熟练掌握三角形的高、中线、角平分线、中位线、中垂线的重要性质,尤其要注意与中点有关的几条线的区别和联系.
变式:(2016·达州)如图3,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为().

图3
A.2B.3C.4D.5
【解析】已知AF⊥BF,AB=10,D为AB中点,根据直角三角形斜边上中线是斜边的一半,可得DF=12AB=AD=BD=5,且∠ABF=∠BFD,又因BF平分∠ABC,可得∠CBF=∠DFB,即DE∥BC,可判定△ADE∽△ABC,根据相似三角形的对应边成比例或者中位线的性质,可得DE=8,所以EF=DE-DF=8-5=3,答案选B.
【点评】当中点出现在直角三角形斜边上时,就要联想到直角三角形斜边上的中线的性质,结合相似得到三角形中位线,很好地将三角形的重要线段整合在一起.
二、几类特殊三角形的知识
例3(2016·鄂州)如图4,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点.当△APB为直角三角形时,AP=.
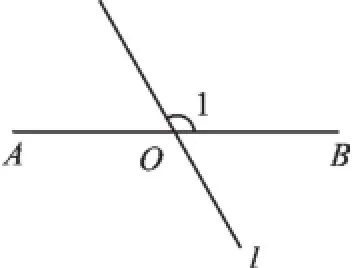
图4
【解析】直角三角形是有一个角为直角的三角形,当△APB为直角三角形,则每个顶点所在的角都有可能为直角,确定P点在直线l上的位置是解决本题的关键.
要使△APB为直角三角形,我们就联想到以AB为直径的外接圆,但AB也有可能为直角边,所以要分类讨论.我们将满足条件的P逐一画在图上.如图5,P1,P2在以O为圆心的外接圆上,P3,P4在⊙O的切线上,再根据题目的已知条件逐一解答即可.故本题分以下3类情况讨论:

图5


【点评】本题考查了外接圆、切线、直角三角形的判定、勾股定理、三角函数、分类讨论思想.本题难度虽然不大,但容易遗漏,要注意分类讨论思想的运用.四种情况中,有两种情况的结果相同.
例4(2016·怀化)等腰三角形的两边长分别为4cm和8cm,则它的周长为().
A.16cmB.17cm
C.20cmD.16cm或20cm
【解析】等腰三角形是有两条边相等的三角形,相等的两边可以是4cm或是8cm,故需要分类讨论.分腰长为4cm或腰长为8cm两种情况:当腰长是4cm时,则三角形的三边是4cm,4cm,8cm,因为4cm+4cm=8cm不满足三角形的三边关系,所以此种情况应舍去;当腰长是8cm时,三角形的三边是8cm,8cm,4cm,三角形的周长是20cm.故答案选C.
【点评】本题容易出错的地方在于,一是忘了分类讨论,漏掉情况;二是分类讨论后忘了用隐含的三角形三边关系来验证是否能构成三角形.熟练运用等腰三角形的性质和三角形三边关系是解题关键.
三、两个三角形的关系
例5(2016·永州)如图6,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD().

图6
A.∠B=∠CB.AD=AE
C.BD=CED.BE=CD
【解析】已知AB=AC,∠A为公共角,选项A,添加∠B=∠C,根据“ASA”即可证明△ABE≌△ACD;选项B,添加AD=AE,根据“SAS”即可证明△ABE≌△ACD;选项C,添加BD=CE,由等量关系可得AD=AE,根据“SAS”即可证明△ABE≌△ACD;选项D,添加BE=CD,因为“SSA”不能证明△ABE≌△ACD,所以此选项不能作为添加的条件,故答案选D.
【点评】全等三角形的判定方法中,尤其要小心两边一角对应相等时,如那对角不是夹角,是不能证明两个三角形全等的.但是特别的,在直角三角形中,两边一角中的那对相等的角可以不是夹角,此时用直角三角形特有的“HL“可以证明两个三角形全等,需要我们好好辨析.
例6(2016·新疆生产建设兵团)如图7,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是().

图7
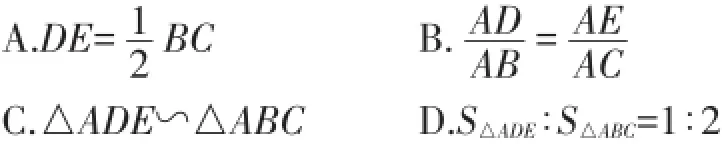
【解析】已知D、E分别是AB、AC的中点,根据中位线的性质定理得到DE∥BC,DE=,再根据平行线分线段成比例定理可得,所以△ADE∽△ABC,再由相似三角形的性质可得以A,B,C正确,D错误,故答案选D.
【点评】相似三角形的判定及性质灵活运用,尤其要注意相似三角形的对应边的比、周长比都等于相似比,而面积比是相似比的平方,本题选项D就是错在面积比还是等于相似比.
四、两个三角形的运动变换
图形的平移、翻折、旋转三种运动变换只改变图形的位置,不改变图形的形状、大小,即运动前后的两个图形全等,因此我们把这三种变换称为全等变换.全等变换的图形,变换前后对应线段、对应角分别对应相等.我们还要掌握平移、旋转、翻折的特征,诸如平移的方向、距离,旋转的方向、旋转角等,熟悉概念和对应关系是解决此类问题的关键.
例7(2016·新疆生产建设兵团)如图8所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是().角就是旋转角,可得旋转角是∠CAC′=180°-30°=150°,故答案选D.

图8
【点评】本题要分清边角的对应关系,并理解旋转角的概念,切勿将∠CAB′看成旋转角.
我们不难发现,在各地中考中,“三角形”是必考内容,难度系数有大有小,覆盖面也非常广,既注重基础知识和基本技能的考查,又有基本思想的渗透、基本活动经验的感悟,体现对大家动手能力、空间想象能力、创新意识的考查,因此,我们既要融会贯通地将这部分专题中的知识点整合在一起,由面到线再到点逐步细化、丰富,并能用好几何语言、图形语言、文字语言三种语言,学会以基本思想为引领,灵活运用本专题相关知识、技能,更有效地解决相关问题.在复习备考中,我们要观察更仔细,下笔多分析、多创新,不断提高数学素养,才能游刃有余地迎战中考.
(作者单位:南京师范大学附属苏州石湖中学)

A.60°B.90°C.120°D.150°
【解析】根据旋转角的定义,两对应边的夹
