综合应用幂的运算法则
2017-04-20
综合应用幂的运算法则
徐爱明
幂的运算是代数演算的重要基础,同学们不仅要熟练掌握幂的运算法则,还要领会幂的运算法则的内涵.现选择几道中考试题和同学们一起赏析.
例1对实数a、b,定义运算☆如下:
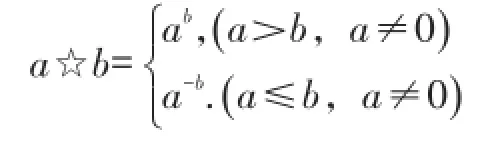
例如:2☆3=2-3=18.
计算:[2☆(-4)]×[(-4)☆(-2)]=.
【分析】根据算式a☆b中a与b的大小,选择定义运算中相应的运算法则进行计算.
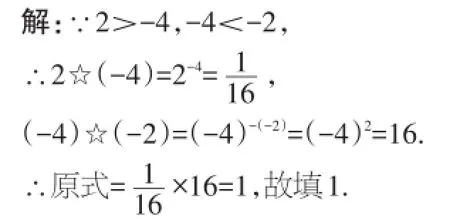
【评注】解答此类问题的关键是正确理解新定义运算,进而将新定义运算转化为幂的运算求解.
例2比较255、344、433的大小,结果是().
A.255<344<433
B.433<344<255
C.255<433<344
D.344<433<255
【分析】观察发现,指数55、44、33都是11的倍数,考虑逆用幂的乘方的法则,将255、344、433化成指数相同的幂的形式,将问题转化为比较底数的大小求解.
解:255=25×11=(25)11=3211,344=34×11=(34)11= 8111,433=43×11=(43)11=6411,
∵32<64<81,
∴255<433<344,故选C.
【评注】本题考查了幂的乘方法则,解答关键是将各个数转化成相同指数的幂的形式,进而转化为比较底数的大小.
变式1:已知x3=2,求x9的值.
解:x9=(x3)3=23=8.
变式2:已知x3=2,求x2∙x+x4∙x2的值.
解:x2∙x+x4∙x2=x3+x6=x3+(x3)2=2+22=6.
【评注】以同学们目前掌握的知识难以由x3=2求出x的值,因此运用整体思想求解,即将x9用含x3的式子表示出来,然后代入求值.
【拓展】已知x、y满足x+2y+1=0,
(1)求2x+2y的值;
(2)求2x∙4y的值.
【分析】(1)利用整体思想,将x+2y看成一个整体求解;(2)先化成同底数的幂,然后运用幂的运算法则计算,最后利用整体思想求解.
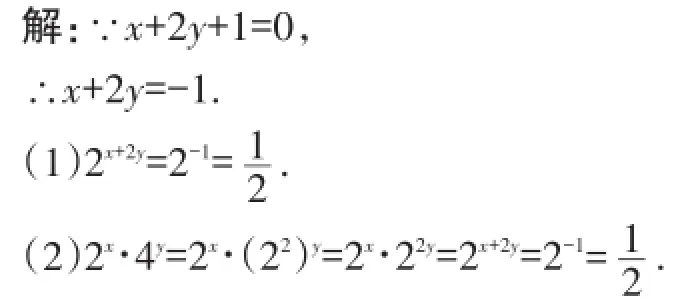
【评注】运用整体思想是求解此类求值题的关键所在.
例3如果等式(2a-1)a+2=1,则a的值为
.【分析】幂等于1的情形有三种:①a0=1(a≠0);②1n=1(n为整数);③(-1)n=1(n为偶数).
解:当a+2=0,即a=-2(满足2a-1≠0)时,(2a-1)a+2=1.当2a-1=1,即a=1时,(2a-1)a+2=1.当2a-1=-1,即a=0时,(2a-1)a+2=1.综合知,a的值为-2、1、0.
【评注】解答本题容易出现遗漏,特别是第三种情形.
江苏省盐城市尚庄初级中学)
延伸阅读
二进制记数法
随着社会的进步,数学记数法也在不断地发展,让我们一起去了解在这演变过程中的一个记数法——二进制记数法.二进制记数法,是以2为基数的基数记数法,所用的数位为0、1,权是2的整数次幂.权就是进制的基底的n次幂,如二进制的权就是2n了.17世纪后半叶,德国数学家莱布尼茨,结合中国的阴阳学说进一步完善了二进制.在二进制中,他形象地用1表示上帝,用0表示虚无,上帝从虚无中创造出所有的实物,恰好在数学中用1和0表示了所有的数.在二进制中,只有两个数码:1和0,其他任何数都用一行0,1表示,加法和乘法规则仅由1+0和1×0组成.
二进制一出现,就深受科技界的欢迎,因为它使运算更加方便.随着电子计算机的广泛应用,二进制进一步大显身手.因为电子计算机是用电子元件的不同状态来表示不同的数码.如果要用十进位制就要求元件能准确地变化出十种状态,这在技术上是非常困难的.而二进制只有两个数码1和0,只需要两种状态就能实现.正如一个开关只有“开”和“关”两种状态一样.如果用“开”表示0,“关”表示1,那么一个开关的两种状态就可以表示一个二进制数,五个开关就可以表示五个二进制数,这样运算起来就非常方便.顺便提一下,二进制数可以根据不同的需要转换为八进制、十进制、十六进制数.
