做一题 会一类——“幂的运算”常见题型训练

做一题 会一类
——“幂的运算”常见题型训练

魏先华

做完一道数学题后，我们要进行反思，如对方法进行总结，本题运用了哪些知识点，有哪些数学思想等，这样可以以点带面，进而触类旁通，解决与此类似的问题.下面以幂的运算为例予以说明.

一、运用幂的运算法则计算

1.做一题.

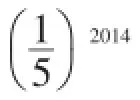
2.方法总结.

两个幂数式相乘时，如果指数较大，而底数的乘积为1或-1时，那么可把指数较大的幂数式逆用同底数幂的乘法运算法则转化为两个幂数式的积的形式，使得其中一个幂数式的指数与原式中较小的指数相同，再逆用积的乘方运算性质把指数相同的两个幂数式的底数相乘，从而简化运算.

3.会一类.

你会解答下列问题吗？

（1）若a、b互为倒数，则a2015×b2016=.

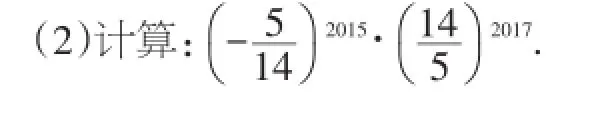
二、运用幂的运算性质求字母的值

1.做一题.

例2计算：若2x∙2x+1=8，试求x的值.

思路探究：运用幂的乘法运算性质解题.由8=23，得2x∙2x+1=23.根据同底数幂的乘法性质，得2x∙2x+1=22x+1.再根据相等的幂的底数相同时指数相等，得2x+1=3，问题获解.

解：∵2x∙2x+1=8，

∴22x+1=23.

∴2x+1=3.

解得x=1.

2.方法总结.

运用幂的运算性质解决求值问题时，要注意分析等式左右两边的式子，如果底数不同，通常将等式左右两边的式子转化成同底数幂的形式，再利用幂相等指数也相等解题.

3.会一类.

你会解答下列问题吗？

（1）若8×2n+1=210（n为正整数），则n=.

（2）已知3×9m×27m=316，求m的值.

三、运用幂的运算性质求代数式的值

1.做一题.

例3计算：已知3m=5，3n=4，求33m-2n的值.

思路探究：先将33m-2n变形为33m÷32n，逆用幂的乘方运算法则将33m变形为（3m）3，32n变形为（3n）2，然后再代入计算.

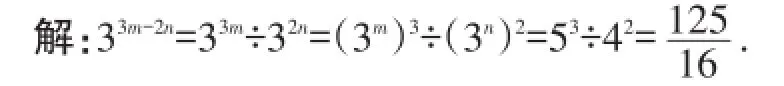
2.方法总结.

逆用幂的除法（或乘法）运算法则，可将指数相减（或相加）的幂转化成同底数幂的相除（或相乘）的形式，逆用幂的乘方运算法则可将指数相乘的幂转化成幂的乘方形式，最后利用整体思想将已知数值代入即可求解.

3.会一类.

你会解答下列问题吗？

（1）若2m=5，2n=6，则2m+2n=.（2）若2m=3，4n=8，求23m+2n-1的值.

四、含零指数和负整数指数幂的计算

1.做一题.

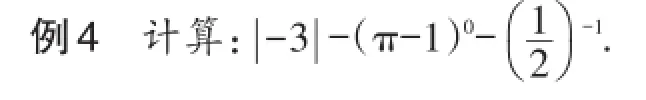
思路探究：应用零指数幂、负整数指数幂的公式求解.

（1）零指数幂的公式是a0=1（a≠0）；

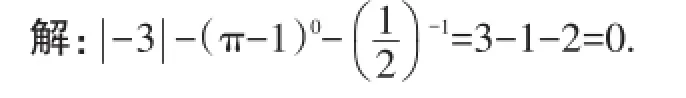
2.方法总结.

3.会一类.

你会解答下列问题吗？

（1）若（x-3）0-2（3x-6）-2有意义，则x的取值范围是（）.

A.x＞3

B.x＜2

C.x≠3或x≠2

D.x≠3且x≠2

则a、b、c、d的大小关系为（）.

A.a＜b＜d＜c

B.b＜a＜d＜c

C.a＜d＜c＜b

D.c＜a＜d＜b

江苏省盐城市大冈初级中学）