基于悬链线的系泊系统优化设计
2017-04-20沈祺欣陈雪蔡志超
沈祺欣++陈雪++蔡志超


摘 要:运用悬链线、几何受力分析、非线性约束优化等方法求解基于悬链线的系泊系统优化设计的3个问题,得到在给定条件下,系泊系统的状态数据以及在未定条件下怎样选择最优锚链、重物球配置来设计系泊系统。利用躺底和不躺底的悬链线公式,计算出使锚链躺底的临界风速ν0,再根据锚链的不同形态,对两种风速下的系统,借助于非线性方程组计算求解,通过建立非线性约束优化模型,求出重物球质量m1上下限。而在极端条件下,重新整合目标函数和约束条件,获得新的多目标非线性约束优化模型,把吃水深度和钢桶倾斜角度作为约束条件,用浮标游动区域为目标对模型优化。
关键词:系泊系统 悬链线 受力分析 非线性方程组 非线性约束优化 多目标优化模型
中图分类号:P751 文献标识码:A 文章编号:1674-098X(2016)12(a)-0055-03
近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成。如图1所示,浮标系统可简化为底面直径2 m、高2 m的圆柱体,浮标质量1 000 kg。系泊系统由钢管、钢桶、重物球、锚链和锚组成,锚质量600 kg,钢管共4节,每节长1 m直径50 mm,每节质量10 kg,要求锚链末端与锚链接处切线方向与海床夹角不超过16°。水声通讯系统安装在长1 m、外径30 cm的密封圆柱形钢桶內,设备和钢桶总质量100 kg,钢桶上接第4节钢管下接锚链,钢桶竖直时,水声通讯设备工作效果最佳,若钢桶倾斜,则影响设备工作效果,钢桶倾斜角超过5°时,设备工作效果较差,为控制钢桶倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
1 分析
该系统优化设计类似一个悬链线模型,但与普通的悬链线模型又有不同,其主要分为两部分,钢桶以下连接锚链可看成悬链线模型;钢桶以上连接4根钢管,需单独分析。问题一,首先,建立平面直角坐标系并对系统各部受力进行分析;如图2所示,要考虑系统临界状态,计算出使锚链是否躺底的临界风速ν0;最后根据锚链的不同形态,对两种风速下的系统,借助于非线性方程组计算求解。问题二利用一种所得模型,直接解出风速为36 m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域,再通过建立非线性约束优化模型,求出重物球质量m1下限。根据浮标恰好浸没于海平面时的受力分析,求出重物球质量m1上限。问题三采用极限思想的方法,假设风速和海水速度均达到最大值,取水深16 m和20 m的两种情况,利用问题二的模型,重新整合目标函数和约束条件,获得新的多目标非线性约束优化模型,然后对模型计算求解。
1.1 系统各部受力分析
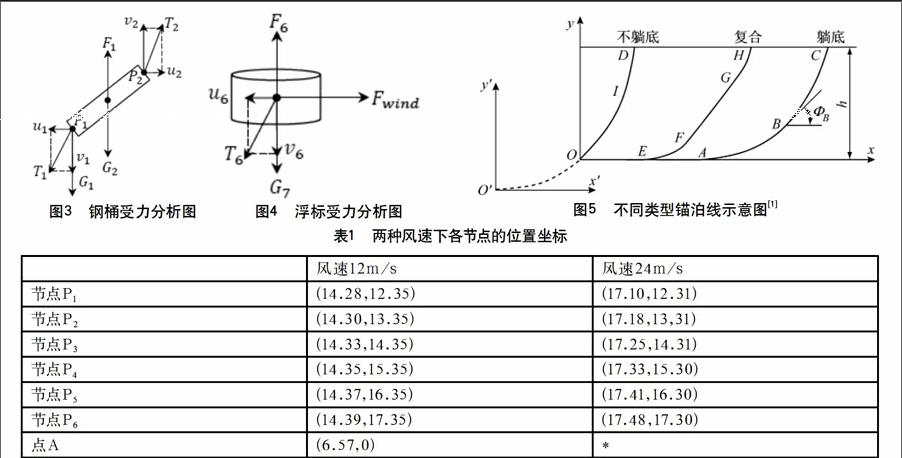
对系统进行受力分析,建立方程求解,对每一个力F建立坐标,进行关于水平方向和竖直方向的正交分解。接下来自下而上对系统内各部分进行受力分析。以钢桶为例,得到如下受力分析图如图3、图4所示。
各分力在水平和竖直方向受力平衡,桶长度为1 m,以及以P1点作为基点分析力矩平衡,可列出如下方程组:
4根钢管与此类似,而浮标的方程组如下:
1.2 悬链线计算公式
根据文献[1]可知,常见有3种悬链线构型及张力分布情况如图5所示。
躺底的悬链线计算公式[1]:
不躺底的悬链线计算公式[1]:
2 求解
2.1 判断临界值求解问题一
把倾角5°作为一个限制条件,假设极端情况——钢管与钢桶全都成一条直线,这样计算出的误差值Δd为0.019 m.可见即使在钢管和钢桶都倾斜5°的情况下,竖直高度误差也是极小的。把浮标以下所连物体都看成一整体,则参照浮标受力分析图解出临界风速:ν0=22.3 m/s(如图6所示)。
图6 浮标下钢管坚直与倾斜的高度差
最后两种风速下的情况分别套用躺底和不躺底的公式,联合其他条件用Mtalab中的fsolve函数就能求出结果见表1所示。
2.2 用非线性约束优化模型求解问题二
下限质量的求解其实可以在问题一模型的基础上,附加一组约束条件,形成一个非线性约束优化模型。为此,只要找出问题二需要的目标函数,即:minG1。给出的限制条件为钢桶倾斜角度θ5不超过5°,锚链在锚点与海床的夹角α不超过16°。结合钢桶受力分析图,得到如下不等式约束:
由于36 m/s时锚链同样不躺底,与24 m/s情况相同,所以我们仍采用未躺底的悬链线计算公式。结合上文受力分析所得的非线性方程组,整合方程组即为我们需要的等式约束条件.用Matlab中的fmincon函数求解得:重物球质量m1下限2 045.8 kg;根据浮标恰好浸没于海平面时的受力分析,求出重物球质量m1上限6 109 kg。
2.3 多目标非线性约束优化求解问题三
新的优化模型有3个目标函数,即minχ6、minθ5和minθ5。但由于多目标优化问题求解困难,考虑到问题中的要求(钢桶倾斜不超过5°,浮标必须露出海面),我们将其中两个目标转化为约束条件,即将吃水深度和钢桶倾斜角度转化为约束条件.这样游动区域就成了唯一的目标函数,即:minχ6。
3 结语
我们主要建立的是一个静力平衡模型,从水平方向、竖直方向来分析受力平衡,通过位置与力分析力矩平衡,建立非线性方程组,最终解得所有未知量。我们还建立了非线性约束优化模型,求出了最优解。对于最后一问,我们将多目标优化模型,将其中的两个目标转换为约束条件。在处理过程中,我们忽略了海水对锚链的作用力,存在一定误差。
多目标优化模型在当今社会的生活中很有非常广泛的应用,比如:有时候我们既想要获得最小风险又想要获得最大收益,对此我们就可以运用多目标优化模型进行解答。
参考文献
[1] 袁梦,范菊,朱仁传,等.基于悬链线理论的系泊系统势能[J].上海交通大学学报,2011,45(4):597-603.
[2] 王丹.一般状态下悬链线方程的应用[J].航海工程,2007,36(S):26-28.
