基于灰狼优化算法的光伏阵列局部阴影下最大功率点跟踪

侯文宝, 张 刚, 田国华

(1. 江苏建筑职业技术学院, 江苏 徐州 221116； 2. 中国矿业大学 信息与电气工程学院,江苏 徐州 221008； 3. 江苏建筑节能与建造技术协同创新中心, 江苏 徐州 221116)

基于灰狼优化算法的光伏阵列局部阴影下最大功率点跟踪

侯文宝1,2,3, 张 刚2, 田国华3

(1. 江苏建筑职业技术学院, 江苏 徐州 221116； 2. 中国矿业大学 信息与电气工程学院,江苏 徐州 221008； 3. 江苏建筑节能与建造技术协同创新中心, 江苏 徐州 221116)

提出一种基于灰狼优化算法的控制方法,以解决光伏阵列局部遮阴下的最大功率跟踪问题。实验结果表明,相比于传统多峰跟踪算法,所提出的算法具有更高的效率和更好的稳定性,同时降低了系统输出信号畸变，且在不同光伏阵列结构及阴影状态下都表现出优越的控制性能。

灰狼优化算法； 光伏阵列； 局部阴影； 最大功率点跟踪

光伏发电作为绿色能源受到国家政策的大力支持,备受关注且推广迅速。光伏电池应用中的最大功率点跟踪是其实际应用必须要克服的问题,且已有多种方法实现对其输出功率的最大功率点跟踪[1-2]。实际使用中的光伏阵列系统,因包含多个独立光伏电池,所以在出现局部阴影时其输出功率曲线呈多峰状态,传统的爬坡法、电导增量法、扰动观察法无法准确定位全局最大功率点[3-5]。粒子群算法可以实现多峰跟踪,但其对系统参数有较大依赖性,且系统状态突变时动态响应效率较低[6]。遗传算法可以实现并行搜索,能够较快地搜寻全局最优解,但是局部搜索能力差,容易导致早熟[7]。这2种方法通常需要引入其他优化以提高搜索精度[8-9]。

鉴于此,本文提出基于灰狼优化算法(grey wolf optimization, GWO)的光伏阵列最大功率点跟踪,以求实现更高效、稳定、优质的全局最大功率点搜索。

1 局部阴影下的光伏阵列特性

光伏电池可以等效为与一个二极管并联的恒流源[10],光伏电池的电流I输出可以表达为

(1)

式中,Ipv为光伏电池输出电流；V为光伏电池单元的输出电压；Rs是由材料电阻、薄层电阻、电极接触电阻及电极本身传导电流的电阻所构成的总串联电阻；Rp为旁路电阻；I0为饱和电流；a为二极管因子；ks为玻尔兹曼常量；q为电荷量；T为开氏温度；Ns为串联电池个数。

光伏阵列是将若干光伏电池模块串联以提高输出电压等级,或并联以提高输出电流等级。因此当光伏阵列出现局部阴影时,其功率-电压(P-V)特性曲线将会出现多峰[11]。当光伏电池工作在串联状态下时,其光伏阵列的等效结构及阴影下的P-V特性曲线见图1；工作在并联结构下的光伏阵列及阴影下的P-V特性曲线见图2,图中Vpv为电池组的输出电压。

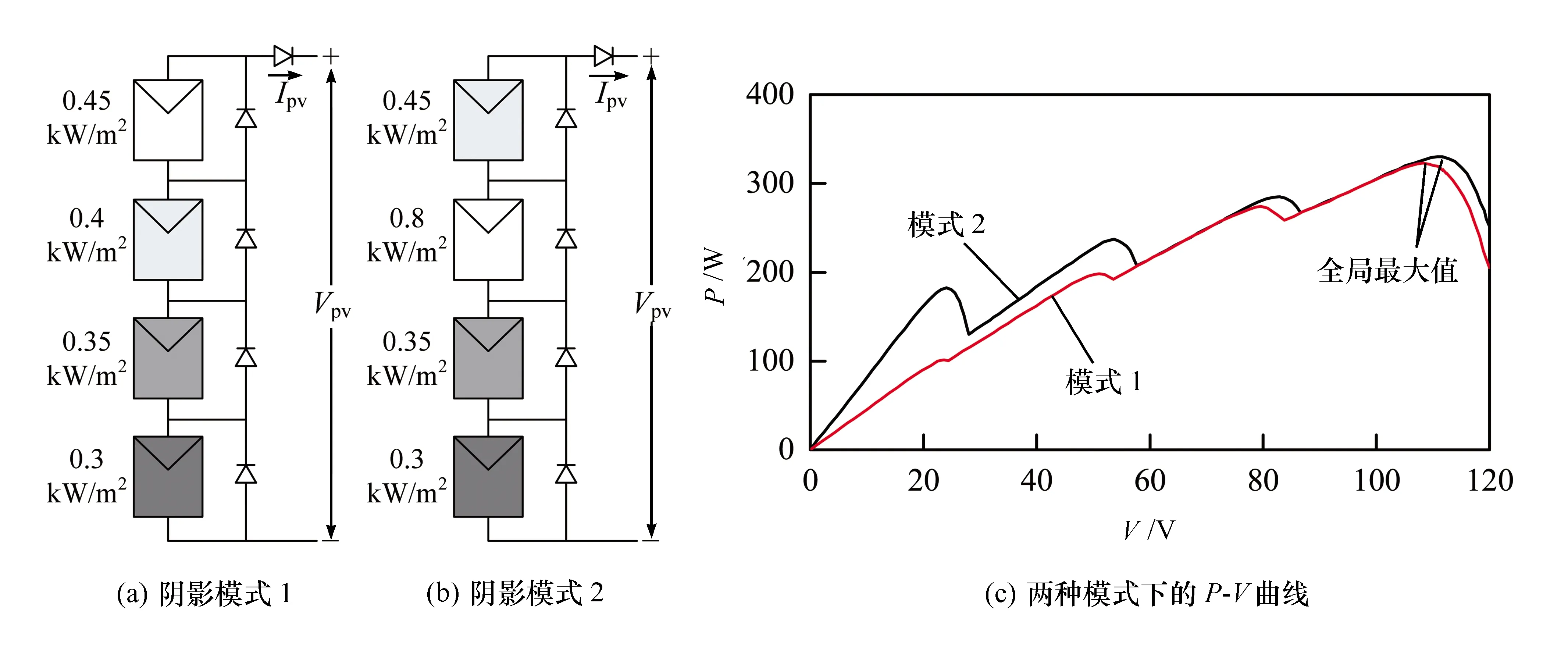
图1 串联光伏阵列系统结构及P -V曲线

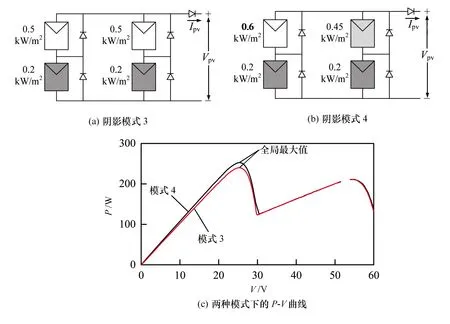
图2 并联光伏阵列系统结构及P -V曲线

2 基于灰狼优化算法的最大功率点跟踪

GWO是模仿自然界中灰狼群的领导结构和捕猎机制,模型假定灰狼群是生活在食物链的顶端且群居[12]。将狼群中的灰狼分为α、β、δ和ω4类,来模拟狼群的领导结构,如图3所示。

图3 灰狼的领导结构

为了对灰狼优化建立数学模型,令α为最优解,则β为次优解,依此类推。灰狼捕猎过程可以分为追踪猎物、包围猎物、攻击猎物。其由追踪到包围行为可以建模如下:

(2)

(3)

式中,t为迭代次数,D、A和C为系数向量,Xp表示猎物的位置向量,X为灰狼的位置向量。向量A和C可通过下式计算:

A=2a·r1-a

(4)

(5)

式中,a在迭代期间从2到0线性递减；r1及r2为[0,1]区间的随机向量。

灰狼捕猎行为由头狼α领导,β和δ跟随并参与狩猎,δ和ω负责照顾伤员。因此可以假设头狼α能够准确判定猎物位置,当猎物位置被确定后,灰狼群群起而攻完成狩猎行为。

基于GWO的最大功率点跟踪控制结构框图如图4所示,此结构与常规结构无异。灰狼数量在系统结构中以占空比的形式表现。根据灰狼优化算法设计的最大功率点跟踪算法流程图如图5所示,图中Gmax为GWO算法的最大功率点，Pmax为实际最大功率。

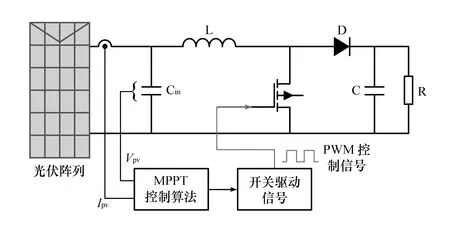
图4 基于狼群算法的最大功率点跟踪控制框图

在局部阴影期间,光伏阵列的输出P-V曲线上存在多个峰值,但仅有一个为全局最大值,其余为局部极值点。当狼群搜寻到最大功率点后,其相关的系数向量自动逼近于0。因此需要在此算法的基础上结合直接占空比控制,即当处于最大功率点时,输出占空比保持恒定以降低稳态系统的输出谐波含量,同时降低因系统振荡引起的功率损耗。将占空比和灰狼优化算法结合,则占空比D定义为灰狼数量。则(3)式可以修正为

(6)

因此GWO的适用函数定义为

(7)

式中,P为功率因数；d为占空比；i为当前的灰狼数量；k为迭代次数。

图5 灰狼优化最大功率点跟踪流程图

3 实验分析

为了验证GWO的正确性,将GWO、改进的粒子群算法(IPSO)以及扰动观察法进行实验对比,并在图1和图2中的两种阵列结构上分别进行实验。实验采用4块额定功率为40 W的电池板组成阵列,其额定参数:最大功率点额定电压Vmp=17.15 V,最大功率点额定电流Imp=2.33 A,开路电压Voc=21.2 V,短路电流Isc=2.55 A。采用不同透光率的塑料板进行遮挡以造成阴影环境。

串联模式下进行不同阴影模式的切换对比实验,以图1串联拓扑为基础,不同的阴影遮挡方式分别形成阴影模式5及阴影模式6两种输出结果。初始状态为模式5,其全局最大值为113.8 W,且包含2个局部极值点；切换后的模式6的全局最大值为143.5 W以及1个局部极值点,如图6(a)所示。分别采用GWO、IPSO以及扰动观察法进行实验,结果分别见图6(b)—(d)。由图6(a)可知,当工作在模式5时,GWO和IPSO可以准确搜索到全局最大功率113.8 W,而扰动观察法搜索到了第一个局部最大值53.44 W。由示波器可知,GWO用时3.18 s,明显短于IPSO的7.9 s用时。当光伏阵列从模式5切换到模式6时,GWO和IPSO可以再次准确搜索到全局最大功率143.5 W,而扰动法仅能搜索到局部极值点65.32 W。

图6 串联光伏阵列输出P- V曲线及实验结果

为了验证此算法在不同结构的光伏阵列上依然有效,选择了图2所示的阵列结构(并联结构)进行了对比实验。在两种不同的阴影模式7和阴影模式8下的输出P-V曲线见图7(a),3种算法的实验结果分别如图7(b)—(d)所示。由图7(a)可知,在阴影模式7下,

3种方法都可以定位到全局最大功率点77.98 W,其中扰动观察法仅是巧合。当从阴影7切换到阴影8时,GWO和IPSO都可再次跟踪到全局最大值58.25W,但GWO耗时仅为IPSO的1/3。而扰动观察法不能定位到全局最大值,搜索的极值点为46.64 W。

图7 并联光伏阵列输出P- V曲线及实验结果

以上实验输出侧负载都为50 Ω电感,当负载为R、L时,且工作在阴影5下,采用GWO算法的实验结果如图8所示。实验结果表明,不同的负载下此算法依然可以准确搜寻到全局最大功率点。

图8 阴影5下R、L负载实验波形

结合图6—图8可知,GWO算法在不同光伏阵列结构、阴影模式及负载类型下都能准确跟踪到全局最大功率点,跟踪速度更快、系统稳定性高且稳态时系统输出信号畸变更低。

4 结论

本文为了解决传统光伏阵列局部阴影下最大功率点跟踪效率低、系统振荡等问题,提出将灰狼优化算法应用到光伏阵列最大功率点跟踪中。实验结果表明,相比于常用的改进粒子群算法,灰狼优化算法在光伏阵列多峰最大功率点跟踪中效率更高,且系统稳定性好、畸变率低。

References)

[1] 赵阳, 符强, 王镭, 等. 基于粒子群算法的最大功率点跟踪方法研究[J]. 电力电子技术, 2010, 44(6):32-33, 77.

[2] 张丽萍, 朱尧富, 马立新. 仿真技术在光伏系统功率跟踪中的应用[J]. 实验技术与管理, 2014, 31(8):114-117.

[3] 杨水涛, 张帆, 丁新平, 等. 基于输入-输出参数的光伏电池最大功率控制的比较[J]. 电工技术学报, 2009, 24(6):95-102.

[4] 金福宝, 李钊年, 刘春艳, 等. 光伏系统MPPT跟踪方法的发展研究[J]. 实验技术与管理, 2010, 27(11):311-313.

[5] 周东宝, 陈渊睿. 基于改进型变步长电导增量法的最大功率点跟踪策略[J]. 电网技术, 2015, 39(6):1491-1498.

[6] 崔岩, 蔡炳煌, 李大勇, 等. 太阳能光伏系统MPPT控制算法的对比研究[J]. 太阳能学报, 2006, 27(6):535-539.

[7] 肖俊明, 王东云, 李燕斌, 等. 基于遗传算法的占空比扰动法在MPPT中的应用研究[J]. 电力系统保护与控制, 2010, 38(15):43-46.

[8] 赵玉林, 张冬梅, 马文川, 等. 局部阴影条件下光伏电池多峰值最大功率点控制策略[J]. 东北农业大学学报, 2015, 46(5):89-94.

[9] 叶林, 陈政, 赵永宁, 等. 基于遗传算法-模糊径向基神经网络的光伏发电功率预测模型[J]. 电力系统自动化, 2015, 39(16):16-22.

[10] Chatterjee A, Keyhani A, Kapoor D. Identification of Photovoltaic Source Models[J]. IEEE Transactions on Energy Conversion, 2011, 26(3):883-889.

[11] 冯志诚, 王亚辉, 吴露露, 等. 局部阴影条件下光伏组件性能实验研究[J]. 太阳能学报, 2015, 36(2):392-398.

[12] Mirjalili S, Mirjalili S M, Lewis A. Grey Wolf Optimizer[J]. Advances in Engineering Software, 2014, 69(3):46-61.

Maximum power point tracking under partial shadow of photovoltaic array based on gray wolf optimization algorithm

Hou Wenbao1,2,3, Zhang Gang2, Tian Guohua3

(1. Jiangsu Vocational Institute of Architectural Technology, Xuzhou 221116, China; 2. School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou 221008, China; 3. Jiangsu Collaborative Innovation Center for Building Energy Conservation and Construction Technology, Xuzhou 221116, China)

A control method based on the gray wolf optimization algorithm is proposed to solve the problem of the maximum power tracking under the partial shadow of photovoltaic array. The experimental results show that compared with the conventional multi-peak tracking algorithm, the proposed algorithm has higher efficiency and better stability, and at the same time reduces the system output signal distortion. Moreover, it shows superior control performance under different photovoltaic array structures and shadow states.

gray wolf optimization algorithm； photovoltaic array； partial shadow； maximum power point tracking

10.16791/j.cnki.sjg.2017.03.016

2016-09-19 修改日期:2016-10-28

江苏住建厅科研项目(2015ZD63)；徐州市科技创新专项资金项目(KC15SM028)；江苏建筑节能与建造技术协同创新中心资助项目(SJXTQ1605)；江苏建筑职业技术学院科技项目(JYQZ16-07)

侯文宝(1982—),男,江苏徐州,在职博士研究生,讲师,主要研究方向为分布式光伏发电与微电网技术

田国华(1980—),男,江苏徐州,博士,高级工程师,主要研究方向为新能源和电力节能.

E-mail:h_wb@qq.com；houwenbaocumt@163.com

TM615

A

1002-4956(2017)3-0060-04