不确定条件下的回归模型及其统计推断
2017-04-19林路
林路
(山东大学 金融研究院,山东 济南,250100)
不确定条件下的回归模型及其统计推断
林路
(山东大学 金融研究院,山东 济南,250100)
本文综述在模型误差期望不确定、部分回归函数不确定等情况下,回归建模和相关统计推断等问题。
不确定性;回归;统计推断
回归是统计学中最常见和最实用的统计模型之一,已有很长的研究历史、成熟的理论和方法以及广泛的应用。尽管如此,复杂情况下的回归模型仍然是近代统计学的热门研究课题,近年来出现了诸多新的理论和方法。本文将综述作者自己以及合作者的相关研究进展,主要关注回归模型在误差期望不确定和部分回归函数不确定等情况下,回归建模和统计推断等若干问题。
1 问题的提出
为了提出问题,根据我们的文献[2,4],考虑如下半参数回归模型:
Yi=g(β,Xi)+m(ti)+ηi,i=1,2,…,n,
(1.1)
其中Xi是p维的随机协变量,Yi是实值的响应变量,g(·,·)是已知的回归函数,β是d维的未知参数,m(·)是未知的光滑函数,ti是s维的非随机协变量。假设g(·,·)对响应变量影响较大,m(·)对响应变量的影响较小,而ti维数s较大。在回归建模时,为了回避高维非参数估计,得到简单的且有表达能力的模型,我们往往忽略非参数部分m(·),得到新的回归模型:
Yi=g(β,Xi)+εi,i=1,2,…,n,
(1.2)
其中新的误差项εi=m(ti)+ηi。这时,在新的模型中,由于E[εi]=m(ti),新的误差具有期望不确定性,也就是新的误差的期望是数据向量ti的函数,随着ti的变化而变化。这个特征违背了传统回归模型最基本的假设:误差的期望是常数(往往是零)。可以验证,用传统的估计方法(例如,最小二乘估计),得到的参数β的估计有不可忽略的偏,从而是不相合的。另一个方面,如上回归模型忽略了部分回归函数,得到回归模型具有不确定性。具体地说,条件期望E[Yi|Xi]=g(β,Xi)+m(ti),i=1,2,…,n
(1.3)
随着另一变量ti的变化而变化。我们可以举出更多例子(包括实际例子)说明参数估计的不相合性和模型不确定性是普遍存在的现象(参看文献[2,4])。由于如上参数估计的不相合性和模型的不确定性,进一步的统计推断和模型应用会失去意义,我们需要发展新的建模方法以及统计推断理论和技术。
2 上期望回归
我们需要在如上不确定性条件下,建立确定的回归模型。上期望回归,是一种稳健和相对有效的选择,文献[1,3]提出了上期望回归的思想。假设模型(1.2)的误差εi的分布来自如下集合:
Γ={F1,F2,…,Fk},
(2.1)
其中k可以依赖于样本容量n。在总体水平下,误差ε的上期望定义为:
(2.2)
其中EF[·]表示在分布F下误差的期望。

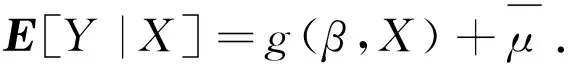
(2.3)
文献[1]证明了,在一定条件下,如上模型是可识别的。例如,在线性模型g(β,X)=βTX下,参数β可以唯一表示为:
β=(E[XXT])-1E{XΕ[Y|X]}-

(2.4)
另外,上期望回归有一定的实际意义,它能描述极端情况下的变量间的回归关系。例如,如果Y表示某种金融产品的风险,X包括相关的财务指标,于是上期望回归(2.3)描述了极端金融环境下的金融产品的最大风险。
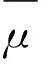
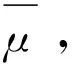
(2.5)
把指标集In={kj:j=1,2,…,n}分解成两个指标集Un={uj:j=1,2,…,[n/2]}和Ln={ls:s=n-[n/2]+1,…,n},满足:In=Un∪Ln,Un∩Ln=∅,uj>ls,uj∈Un,ls∈Ln。记
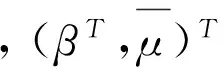
(2.6)

于是,凸优化问题(2.6)渐近等价于如下优化问题:
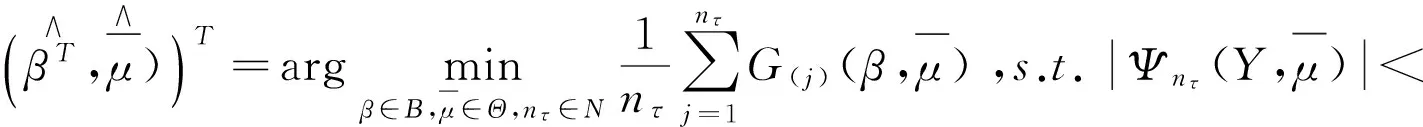
(2.7)
3 Mini-max-risk回归
在不确定性条件下,还可以通过其它方法得到确定的回归模型。文献[4]中定义了mini-max-risk和mini-mean-risk回归。为了简单,本文只介绍mini-max-risk回归。理论上,我们可以定义β为如下上期望损失的解:

也就是说,β可以表示成:
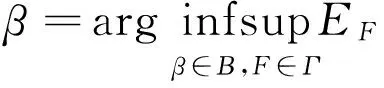
(3.1)
假设如上上期望损失在F*∈Γ达到最大,也就是

(3.2)

其中μ*=EF*[ε]。经过这样的处理,在分布F*下,得到新的回归模型(3.3)是唯一的。我们称此模型为mini-max-risk回归,其理由为,这个模型是通过最小化最大期望得到的。从定义可以看成这样的模型具有稳健性,也就是得到模型有最小的最大风险。
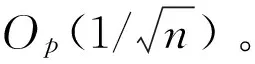
4 上期望的相合估计
上期望回归和mini-max-risk回归都涉及到上期望(最大期望)。上期望是一种非线性期望,也就是不满足可加性。非线性期望理论在概率论领域得到迅速的发展,已有较成熟的理论和方法(参见文献[5-8]),在金融数学和计量经济等领域有着广泛应用(参见文献[9,10])。但是,其统计学方面的应用发展较慢,还在起步阶段,其主要原因如下:可以验证,上期望满足次可加性,也就是对任意随机变量U和V,我们有:
Ε[U+V]≤Ε(U)+Ε(V).
于是,我们不能保证样本均值趋于一个确定值,这违背了同分布情况下的大数定律。事实上,文献[5,6]表明,以大概率有

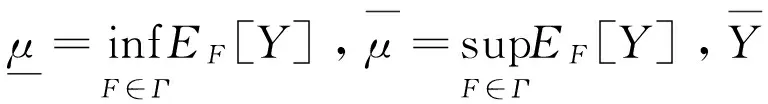

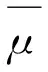

但是,我们发现,尽管估计是相合的,但是其收敛速度依赖于不确定性条件,也就是,不确定性越强,收敛速度越慢。这是非线性期望难以统计应用的另一原因。
总之,不确定情况下的统计分析,是一个新的研究领域,有较多的挑战,也有较大的发展空间和应用前景。
[1]L Lin,S Yang,Y Shi,et al.k-sample upper expectation linear regression[J].Journal of Statistical Planning and Inference,2016,170:15-26.
[2]Lin L,Liu Y and Lin C.Consistent Estimation for Distribution-uncertainty Regressions via Cross-sample and Semiparametric Methodologies[J].2016,manuscript.
[3]Lin L,Dong P,Song Y,et al.Upper expectation parametric regression[J].Personality&Individual Differences,2014,15(6):653-664.
[4]Lin L,Liu Y and LinC.Mini-max-risk and mini-mean-risk regressions under distribution-uncertainty[J].Statistics,2016,to appear.
[5] S Peng.Multi-dimensional G-Brownian motion and related stochastic calculus under G-expectation[J].Stochastic Processes and their Applications,2007,118(12):2223-2253.
[6]S G Peng.Survey on normal distributions,central limit theorem,Brownian motion and the related stochastic calculus under sublinear expectations[J].Science China:Mathematics,2009,52(7):1391-1411.
[7]S Peng.Backward SDE and related g-expectations[J].Backward Stochastic Differential Equations,1997:141-159.

[9]Chen Z,Epstein L.Ambiguity,risk,and asset returns in continuous time[J].Econometrica,2002,70(4):1403-1443.
[10]Z Org.Maxmin expected utility with non-unique Prior[J].Journal of Mathematical Economics,1989,18(2):141-153.
Regression model and its statistical inference under uncertainty
LIN Lu
(Institute for Financial Studies,Shandong University,Jinan 250100,China)
In this paper we investigate regression modeling and related statistical inference under the uncertainties of error expectation and partial regression function.
uncertainty;regression;statistical inference.
1672-7010(2017)01-0001-05
2016-11-29
国家自然科学基金资助项目(11571204,11231005)
林路(1958-),男,湖南武冈人,教授,博士,博士生导师,从事金融统计、高维统计和非参数统计等方面的研究
O212 < class="emphasis_bold">文献标志码:A
A
