求解非线性方程组的加速多步Levenberg-Marquardt算法

苏晨诚，陈 亮

（淮北师范大学 数学科学学院，安徽 淮北 235000）

求解非线性方程组的加速多步Levenberg-Marquardt算法

苏晨诚，陈 亮

（淮北师范大学 数学科学学院，安徽 淮北 235000）

求解非线性方程组时，为了节省Jacobi矩阵的计算，在信赖域中提出一种加速多步Levenberg-Marquardt算法，该算法在每次迭代时不仅计算了经典的LM步，还使用先前计算过的Jacobi矩阵计算三步近似的LM步，节省了计算量，提高了计算效率，数值试验表明，该算法具有有效性.

非线性方程；Levenberg-Marquardt算法；全局收敛性；信赖域

0 引言

考虑非线性方程组

是连续可微的函数.在本文中，定义X*是F(x)的非空解集，‖∙‖表示2-范数，由于的非线性特征，问题（1）可能没有解.

Levenberg-Marquardt（LM）方法［1-5］是求解非线性方程组较为经典的方法之一，其迭代步为

它可以看成是Guass-Newton方法的一种修正，通过引入一个参数λk来克服Guass-Newton法对于矩阵J(x*)必须满秩的要求.

为了节约雅克比矩阵的计算，Fan［6,8］受两步牛顿法的启发，提出了一种改进的LM算法（MLM），该算法不仅计算经典的LM步，还计算一步近似LM步

该算法在局部误差阶条件下具有3阶收敛性.

相似地，为了节约更多的雅克比矩阵的计算以及得到更快的收敛速度，Yang［7］在文献［6］的基础上提出了一个高阶的LM算法（HMLM），又增加了一步近似LM步

该算法在局部误差阶条件下具有4阶收敛性.

Chen［9］为了控制步长，在结合了Fan和Yang思路的基础上，提出一种高阶的修正LM算法受此启发，为了在求解非线性方程组的过程中节约更多的Jacobi矩阵计算，本文将在文献［9］思路的基础上再增加一步近似LM步，

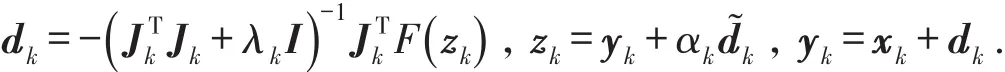
从而得到一种新的加速多步Levenberg-Marquardt算法.

1 加速多步Levenberg-Marquardt算法

首先，通过信赖域的方法给出新的加速多步LM算法，取

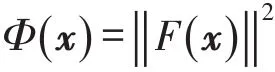
作为式（1）的优值函数，定义Φ(x)的实际下降量为

文献［6-8］已经证明了式（2）—（4）成立

结合不等式（2）—（5）有

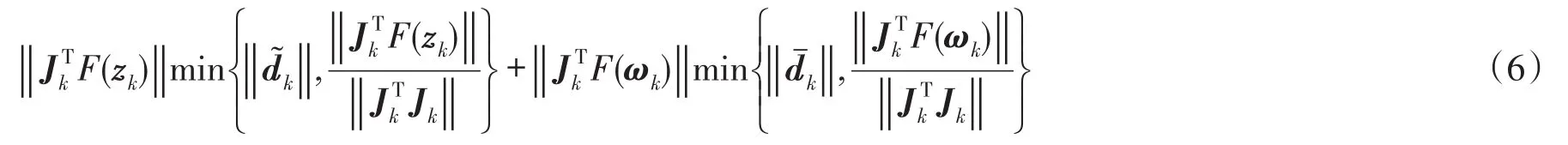
这意味着定义的预测下降量dk一直是非负的.

接下来，给出加速多步Levenberg-Marquardt算法：

算法1 加速多步Levenberg-Marquardt算法（NAMLM）

步骤1 给定x1∈Rn，ε≥0，u1＞m＞0，0＜p0≤p1≤p2＜1，k：=1.

可得dk，令yk=xk+dk.求解

步骤3 计算rk=Aredk/Predk，令

步骤4 取

令k=k+1，转步骤2.

2 加速多步Levenberg-Marquardt算法的全局收敛性

在给出加速多步LM算法的全局收敛性之前，先给出下面一些假设.

假设1 F(x)是连续可微的函数，F(x)和它的Jacobi矩阵是利普希茨连续的，因此，存在正常数L1和L2使得

和

由利普希茨条件可得

定理2 在假设3.1的条件下，加速多步Levenberg-Marquardt算法在有限迭代步将收敛并满足

证明 利用反证法.设定理2不成立，则存在一个正数ε＞0，存在无限多k，使得

令T1，T2是如下指标集

很容易得到T1指标集是无限集，接下来考虑T2指标集是有限集还是无限集.

情形1T2是有限集，则集合也是有限集，令是T3中最大的指标，则当时，有xk+1=xk.定义集合

由（9）式知

因此，由（8）式、（10）式及以上4个不等式可得

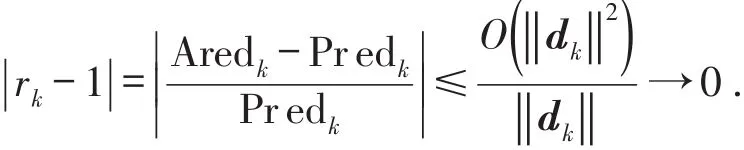
这意味着rk→1，随着 μk的更新知，当k充分大时，存在一个正常数＞m使得 μk＜，这与（13）式矛盾.所以当T2为有限集时，假设不成立.

情形2 T2是无限集，由（6）式和（9）式知

意味着

根据dk的定义，有

通过（8）式，（9）式和（14）—（16）式知

与情形1同理可得rk→1，因此当k充分大时，存在一个正常数＞m使得μk＜，这与（19）式矛盾.

3 数值试验

本节将通过计算一些非奇异问题来测试算法1（NAMLM），并将其与经典LM算法，Fan［8］提出的AMLM算法以及Chen［9］提出的NMLM算法进行比较.

下面的问题是由More等［10］给出的，该问题是通过非奇异问题的修正得来的，并具有如下形式［11］：

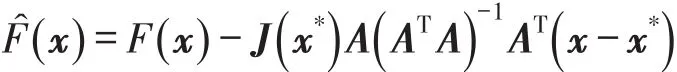
其中F(x)是标准的非奇异函数，x*是它的根，并且A∈Rn×k是满列秩，1≤k≤n.显然，(x*)=0并且秩为n-k，该问题的一个缺点是的根有可能不是的根.本文选择的秩分别为n-1和n-2.

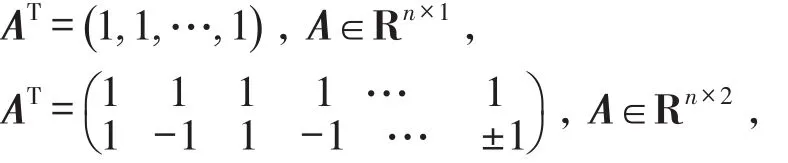
设 p0=0.000 1，p1=0.25，p2=0.75，μ1=10-5，算法的停止条件是或者是迭代次数超过100（n+1），在表1和表2中，第3列表示初始点是x0，10x0，100x0，其中x0是由More等［10］给出的.“NF”和“NJ”分别表示函数的计算量和Jacobi矩阵的计算量，“NF+NJ*n”表示所有的计算量，因为Jacobi矩阵的计算量通常是函数计算量的n倍，如果迭代次数超过100（n+1），用“-”表示.“OF”表示迭代是向上溢出或向下溢出的.

表1 r(J (x*))=n-1

表2 r(J (x*))=n-2

从表1和表2中可以看出，算法1总是优于或相似于LM算法、AMLM算法与NMLM算法，尽管函数的计算量多，但是算法1节约大量的Jacobi矩阵的计算，该算法在现实生活中很有用，特别是对于大规模非线性问题来说.

4 结论

本文在求解非线性方程组的过程中，为了节约Jacobi矩阵的计算以及达到更高的收敛性，提出一种加速多步LM算法，该算法每步迭代不仅计算了LM步也近似计算了三步近似LM步，新的LM算法节约了更多的Jacobi矩阵的计算，对于大规模问题，该算法要比LM算法、AMLM算法以及NMLM算法具有更好的表现形式.

［1］LEVENBERG K.A method for the solution of certain non-linear problems in least squares［J］.Quarterly of Applied Mathmatics，1944，2（1）：164-168.

［2］MARQUARDT D W.An algorithm for least-squares estimation of nonlinear parameters［J］.Journal of the Society for Industrial and Applied Mathematics，1963，11：431-441.

［3］MORÉ J J.The Levenberg–Marquardt algorithm［C］//Lecture Notes in Mathematics，1977，11（1）：101-110.

［4］MORÉ J J.Recent developments in algorithms and software for trust region methods［M］.Springer Berlin：Mathematical Programming the State of the Art，1982：258-287.

［5］CHEN Liang.A high-order modified Levenberg-Marquardt method for systems of nonlinear equations with fourth-order convergence［J］.Applied Mathematics and Computation，2016，24：78-83.

［6］FAN Jinyan.The modified Levenberg-Marquardt method for nonlinear equations with cubic convergence［J］.Mathematics of Computation，2012，81（277）：447-466.

［7］YANG Xiao.A higher-order Levenberg–Marquardt method for nonlinear equations［J］.Applied Mathematics&Computation，2013，219（7）：10682-10694.

［8］FAN Jinyan.Accelerating the modified Levenberg-Marquardt method for nonlinear equations［J］.Mathematics of Computation，2014，83：1173-1187.

［9］CHEN Liang.A modified Levenberg-Marquardt method with line search for nonlinear equations［J］.Computational Optimization&Applications，2016，65（3）：1-27.

［10］MORÉ J J，GARBOW B S，HILLSTROM K E.Testing unconstrained optimization software［J］.ACM Transactions on Mathematical Software，1981，7（1）：17-41．

［11］SCHNABEL R B，FRANK P D.Tensor methods for nonlinear equations［J］.Siam Journal on Numerical Analysis，1984，21（5）：815-843.

An Accelerating Multistep Levenberg-Marquardt Method for System of Nonlinear Equations

SU Chencheng，CHEN Liang
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

In this paper，we present an accelerating multistep Levenberg-Marquardt（NAMLM）method for system of nonlinear equations to save more Jacobian calculations.At every iteration，not only LM step but also three approximate LM steps，which used the previous calculated Jacobian，are computed.The global convergence is given by the trust region technique.Numerical result shows that the accelerating multistep LM algorithm performs very well and save many Jacobian calculations.

nonlinear equations；Levenberg-Marquardt method；global convergence；trust region

O 221.1

A

2095-0691（2017）01-0024-07

2016-09-29

国家自然科学基金项目（61300048）；安徽省自然科学基金资助项目（1508085MA14）；安徽省高校优秀青年人才支持计划；安徽省高等教育振兴计划重大教学改革研究项目（2014ZDJY058）；安徽省省级质量工程项目（2014JYXM161，2015JYXM157）；淮北师范大学校级质量工程项目（2015ZYJS185，JY15118）

苏晨诚（1991- ），女，安徽合肥人，硕士生，研究方向为数值最优化.通信作者：陈 亮（1977- ），男，江苏射阳人，博士，副教授，研究方向为数值最优化.