有限域上negabent函数的若干结论

任明生，卓泽朋，于瑞瑞

（淮北师范大学 数学科学学院，安徽 淮北 235000）

有限域上negabent函数的若干结论

任明生，卓泽朋，于瑞瑞

（淮北师范大学 数学科学学院，安徽 淮北 235000）

讨论一类迹函数表示的布尔函数，利用negabent函数的已有结论，给出该类函数为negabent函数的充要条件.

布尔函数；互相关系数；negabent函数

0 引言

布尔函数在密码学中扮演着重要的角色，特别是在对称密码学中.Rothaus［1］介绍一类bent函数，这类函数在密码学和编码理论中非常重要.虽然许多具体构造的bent函数是已知的，但是一般的bent函数的结构仍不清楚.

如果一个布尔函数的nega-Hadamard变换的绝对值都相等，那么称其为negabent函数.近年来，有很多关于negabent函数的研究成果［2-12］.Stanica等［5-10］给出nega-Hadamard变换特征的详细结果，同时还给出negabent函数分解的一些结论；文献［7］讨论nega-Hadamard变换的结论；文献［8］利用二次丢番图积分方程研究negabent函数，给出判定函数是否为negabent函数的条件和间接构造negabent函数的方法；文献［11］给出含有奇数或偶数个变量布尔函数是negabent函数的充要条件，同时给出一种构造negabent函数的方法.

1 预备知识

设F2表示只有两个元素的有限域.n元布尔函数是映射 f：Fn2↦F2，记Bn为所有n元布尔函数所组成的集合.整数集、实数集和复数集分别用Z，R和C表示.此外，R上的加法记为与Fn2的加法记作⊕，⊕i.元素x中1的个数称为x的汉明重量，记为ωt(x)，即如果一个布尔函数的真值表包含相等个数的0和1，即：ωt(f)=2n-1，说这个布尔函数是平衡的.函数 f(x)和g(x)的距离用d( f,g)表示，也就是 f⊕g，即：d(f,g)=ωt(f⊕g).

设布尔函数 f(x)∈Bn，对于任意x=(x1,x2,…,xn)∈F2n，f(x)∈Bn的代数正规型（ANF）为

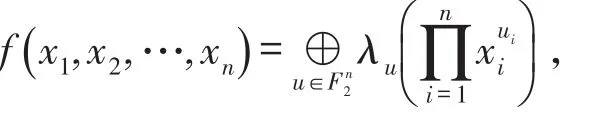
其中λu∈F2，u=(u1,u2,…,un)∈F2n；f(x)的代数次数deg(f)是ANF中变量最多的非零单项式的变元个数.代数次数最多为1的布尔函数称仿射函数，记作An.常数项为0的仿射函数叫做线性函数.在F2n上的任何线性函数都可表示成

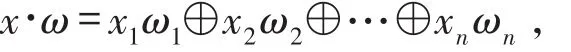
其中x,ω∈F2n.代数次数大于1的布尔函数，称为非线性函数.非线性n元函数 f(x)的非线性度为nl(f)=ming∈An(d ( f,g ))，即到所有 n元仿射函数的最小汉明距离.如果 x=(x1,x2,…,xn)∈F2n和y=(y1,y2,…,yn)∈F2n,，定义的数量积（或内积）为x∙y=x1y1⊕x2y2⊕…⊕xnyn.

f∈Bn在任何点ω∈Fn2的Walsh-Hadamard变换可表示为

f∈Bn在任何点ω∈Fn2的nega-Hadamard变换是复值函数：

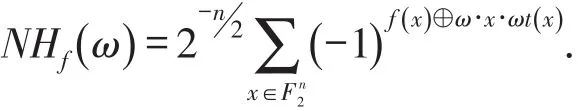
对一个整数n，函数 f∈Bn是bent函数当且仅当对所有ω∈Fn2.类似的，f是negabent函数当且仅当其中ω∈Fn2.如果 f是bent和negabent的，说 f是bent-negabent的.在两种不同的傅立叶变换下，它们具有一些有趣的性质.

负互相关系数 f和g在ω为：

f在ω上的负自相关系数为

定义1 设 f(x),g(x)∈Bn，f(x)和g(x)的负相关平方和指标定义为

如果 f=g，那么Δf,f称为 f的负自相关平方和，即Δf=

注意到，NCf(0)=2n.因此，文献［5，9，10］提到布尔函数 f(x) ∈Bn是negabent函数当且仅当NCf(ω )=0，当所有ω∈F2n-{0}.因此，Δf≥22n,在等式成立当且仅当 f是negabent函数.

2 negabent函数在有限域上的若干结果

本节讨论定义在F2n上的布尔函数，并且描述这些函数的negabent性质.向量空间F2n通过在F2上选择的一个基，可以看作与F2n是等同的.

设2是一个素数的幂，函数Tr:F2n→F2的定义为

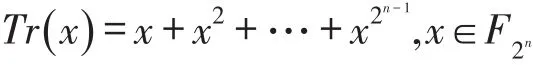
有限域上的加法运算记作“+”.若选择基{α1,α2,…,αn}是自对偶的，那么函数可表示为：

为了给出研究结果，先给出以下引理.

引理1［9，12］函数 f2n:F2→F是negabent函数F2n当且仅当

对任意的ω∈F2*n，其中,F2*

n表示F2n上除0以外其他元素构成的一个乘法群.

文献［13］研究semi-bent序列的具有多于一个迹形式的无限类.例如和本文提出negabent函数的一个充分且必要条件.

注意：当n为奇数（或偶数）时，若布尔函数的Walsh-Hadamard变换仅仅取，则称为semi-bent函数.

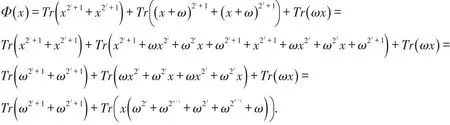
通过引理1，知道函数 f是negabent函数当且仅当对任意的也即是

通过置换多项式的一些知识，也可给出negabent函数的一种刻画.

定理2 设n为偶数，并按定理1的形式定义 f.那么 f是negabent函数当且仅当多项式上的置换多项式.

证明 由定理1，得到 f是negabent函数当且仅当ω2i+ω2n-i+ω2n-j+ω≠0对任意的，这意味着多项式在F2n上没有非零根.注意到P(x)是线性多项式，且线性多项式若为置换多项式当且仅当没有非零根.证毕.

［1］ROTHAUS O S.On“bent”functions［J］.Journal of Combinatorial Theory，1976，20（3）：300–305.

［2］PARKER M G，POTT A.On Boolean functions which are bent and negabent［C］//SABLAVROLLES D.International Conference on Sequences，Subsequences and Consequences.Berlin:Springer-Verlag，2007：9-23.

［3］SCHMIDT K U，PARKER M G，POTT A.Negabent functions in the Maiorana-McFarland class［C］//EMMANUELL Diaz. Sequences and Their Applications-Seta 2008.Lexington:Random House,2008:390-402.

［4］SARKAR S.On the symmetric negabent Boolean functions［C］//EMMANUELL Diaz.Progress in Cryptology-Indocrypt 2009.New Dechi:Springer-Verlag,2009:136-143.

［5］STANICA P，GANGOPADHYAY S，CHATURVEDI A，et al.Nega-Hadamard transform，bent and negabent functions［C］// SABLAVROLLES D.International Conference on Sequences and Their Applications.Berling:Springer-Verlag，2010：376-378.

［6］GANGOPADHYAY S，CHATURVEDI A.A new class of bent-negabent Boolean functions［J］.Iacr Cryptology Eprint Archive，2010，27（3）：32-35.

［7］卓泽朋，崇金凤，魏仕民.Nega-Hadamard变换和negabent函数［J］.山东大学学报（理学版），2013，48（7）：29-32.

［8］REN Chunlun，LIU Fengmei，LI Zhongxian，et al.Some results about negabent functions［J］.Journal on Communications，2011,32（8）：179-182.

［9］SARKAR S.Characterizing negabent Boolean functions over finite fields［C］//SABLAVROLLES D.International Conference on Sequences and Their Applications.Berlin:Springer-Verlag,2012：77-88.

［10］STǍNICǍ P，GANGOPADHYAY S，CHATURVEDI A，et al.Investigations on bent and negabent functions via the nega-Hadamard transform［J］.IEEE Transactions on Information Theory，2012，58（6）：4064-4072.

［11］SU Wei，POTT A，TANG Xiaohu.Characterization of negabent functions and construction of bent-negabent functions with maximum algebraic degree［J］.IEEE Transformation on Information Theory，2013，59（6）：3387-3395.

［12］SARKAR S.Some results on bent-negabent Boolean functions over finite fields［J］.Eprint Arixiv,2014,49(2):2164-2170.

［13］CHARPIN P，PASALIC E，TAVERNIER C.On bent and semi-bent quadratic Boolean functions［J］.IEEE Transactions on Information Theory，2010，51（12）：4286-4298.

Some Results on Negabent Boolean Functions

REN Mingsheng，ZHUO Zepeng，YU Ruirui
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

Discuss the trace function representation of Boolean function.Based on it，some properties on negabent functions are discussed.We present two necessary and sufficient conditions for the decision on negabent function.

Boolean function；cross-correlation coefficient；nega-crosscorrelation coefficient

TN 918.8

A

2095-0691（2017）01-0013-04

2016-08-18

安徽省自然科学基金资助项目（1608085MF143）；安徽高校优秀青年人才支持计划重点项目（gxyqZD2016112）

任明生（1992- ），男，安徽濉溪人，硕士生，研究方向：密码学.通信作者：卓泽朋（1978- ），男，安徽灵璧人，教授，研究方向：密码学.