随机环境中具有配对单元迁移的两性分枝过程的极限性质

任 敏，张光辉

（宿州学院 数学与统计学院，安徽 宿州 234000）

随机环境中具有配对单元迁移的两性分枝过程的极限性质

任 敏，张光辉

（宿州学院 数学与统计学院，安徽 宿州 234000）

文章研究随机环境中具有配对单元迁移的两性分枝过程，在独立同分布的随机环境下，建立具有配对单元迁移的两性分枝过程{Zn,n≥0}且迁移的配对单元数与当前人口数有关，证得此过程是随机环境中的马氏链，并给出每个配对单元平均增长率的极限性质.

随机环境；两性分枝过程；平均增长率；极限性质

0 引言

1968年，Daley首次引入两性分枝过程的模型，随后诸多概率论工作者研究它的极限性质、灭绝概率等问题［1-4］.为描述更复杂的物种模型，一些改进的两性分枝过程模型被引入，如具有迁入的两性分枝过程［5］，配对依赖人口数的两性分枝过程［6］，伴有移民的两性分枝过程［7］，具有配对单元移出的两性分枝过程［8］等等.本文在前人研究基础上，研究随机环境中具有配对单元迁移的两性分枝过程模型，并且迁移的配对单元数和当前人口数有关，给出过程的马氏性和每个配对单元平均增长率的性质，推广经典两性分枝过程的相关结论.

设(Ω,F,P)是概率空间，(Θ,Σ)是可测空间，N是非负整数集，配对函数L(∙,∙):N2→N关于每个分量单调不减且是上可加的.设ξ→={ξ,n≥0}和{(Fn,Mn)}n≥1是定义在(Ω,F,P)上分别取值于(Θ,Σ)和N2的随机变量序列，{(fξn,i,mξn,i)}n≥1是在给定环境ξn下取值于N2的独立同分布的二维随机变量序列.

定义1 若{Zn,n≥0}满足下列条件

（1） Zn=N0∈N，

（2）(Fn,Mn)=

（3）Zn+1=L(Fn+1,Mn+1)+Yn+1(L(Fn+1,Mn+1))

则称{Zn,n≥0}为随机环境中具有配对单元迁移的两性分枝过程，其中 fξn,iIξn,i,mξn,iIξn,i表示第n代的第i个配对单元在环境ξn下生成的雌性个体数和雄性个体数；Fn+1,Mn+1表示第n代所有配对单元生成的雌性总数和雄性总数.在环境ξn下，若第n代的第i个配对单元移出，则Iξn,i=0；若第n代的第i个配对单元不移出，则Iξn,i=1.Yn+1(L(Fn+1,Mn+1))表示第n+1代移入的配对单元数，并且移入的配对单元数与当前配对人口数有关.{Iξn,i,i≥1}在给定的环境ξn下是独立同分布的，且与{fξn,i,mξn,i}i≥1独立.

定义2 若随机环境中的两性分枝过程的配对函数是上可加的，即则称该过程是上可加的.

记Fn(ξ⇀)=(Z0,Z1,…,Zn,ξ0,ξ1,…,ξn,…),n=0,1,2,…,且对任意的x,y∈N,有L(x,y)与Fn(ξ⇀)相互独立.

1 马氏性

定理1.1 设ξ⇀={ξn,n≥0}独立同分布，则{Zn,n≥0}是随机环境中的马氏链，其一步转移概率为

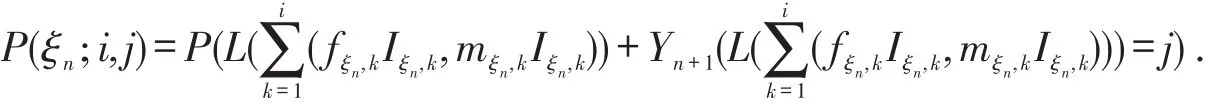
证明 由{Zn,n≥0}的定义知，P(Z0=N0|ξ⇀)=P(Z0=N0|ξ0)，因为L(x,y)与Fn(ξ⇀)相互独立，对任意的i1,i2,…,in-1,i∈N，有

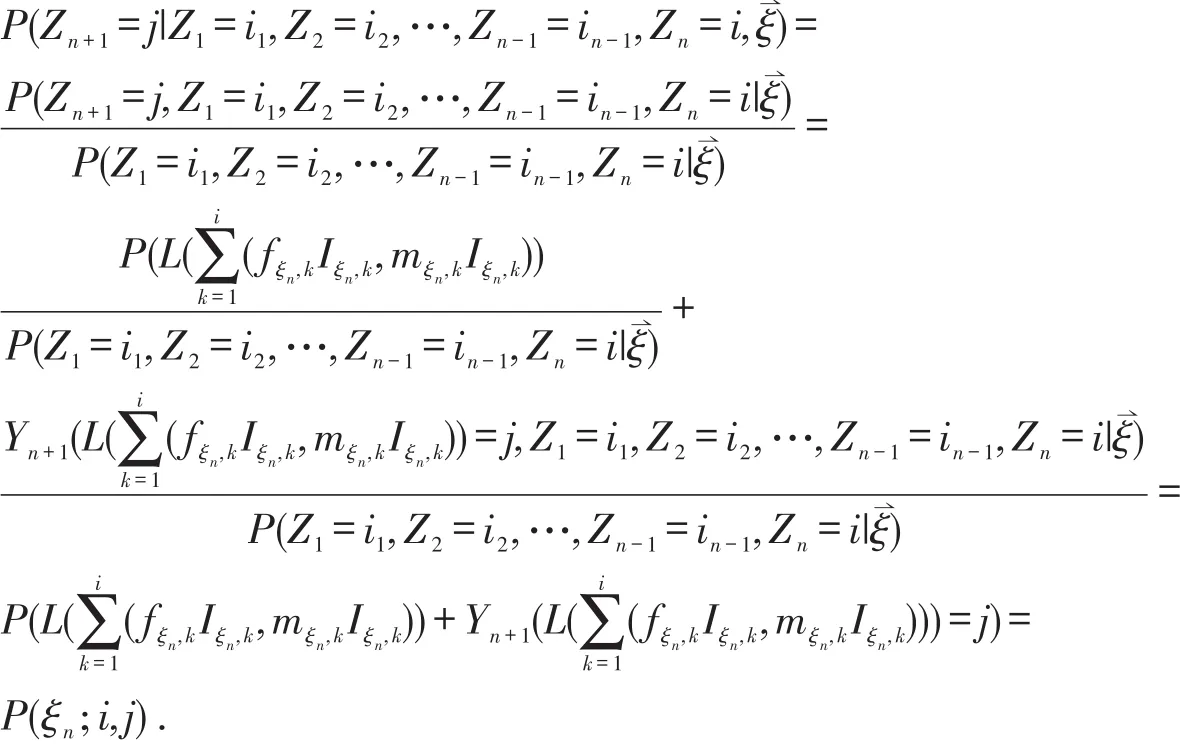
由随机环境中马氏链的定义可知，{Zn,n≥0}是随机环境中的马氏链.

定理1.2 设ξ⇀={ξn,n≥0}独立同分布，则{Fn+1,Mn+1}是随机环境中的马氏链，其一步转移概率是

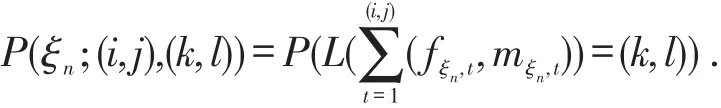
类似于定理1.1可以证得定理1.2.

2 极限性质

定义2.1 设{Zn,n≥0}是随机环境中具有配对单元迁移的两性分枝过程，当其第n代配对单元数为k时，称为第n代每个配对单元的平均增长率.

定理2.1 设随机环境 ξ⇀={ξn,n≥0}是独立同分布，配对函数 L(x,y)是上可加的并且满足L(x,y)≤x+y. 若 {Yn(k)}k≥0满 足 P(Yn(k+1)≤Yn(k))=1,0＜E(Yn(k))＜∞,0＜E(fξn,1Iξn,1,mξn,1Iξn,1)＜∞ ，则

证明 分以下几步证明结论：

第1步，由强大数定律可得，

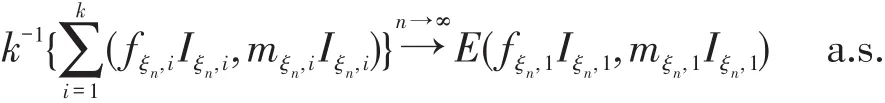
第2步，证明k-1L{k(E(fξn,iIξn,i),E(mξn,iIξn,i))}的极限存在.令ak=k-1L{k(E(fξn,iIξn,i),E(mξn,iIξn,i))},则

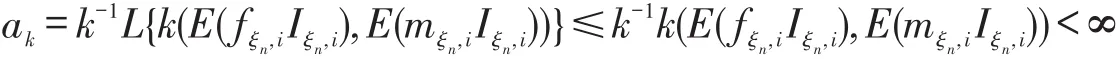
即ak有界，故极限存在且与E(fξn,iIξn,i),E(mξn,iIξn,i)有关，记为

第3步，证明r(x,y)是D={(x,y)|x≥0,y≥0}上的二元连续函数，对任意的ε＞0有

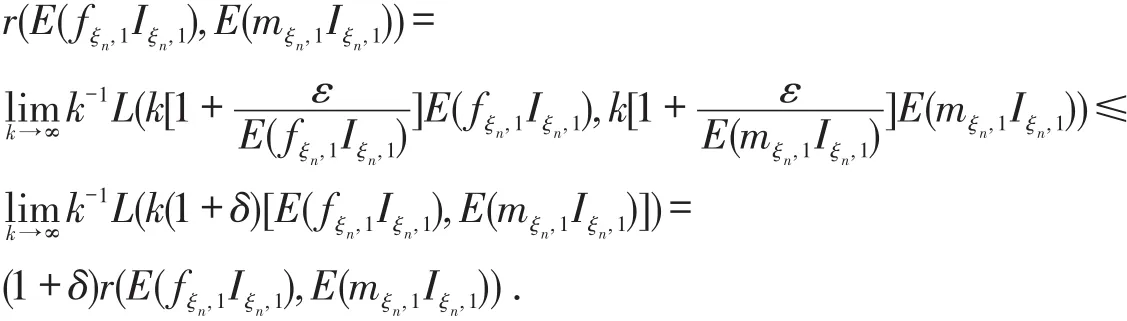
其中

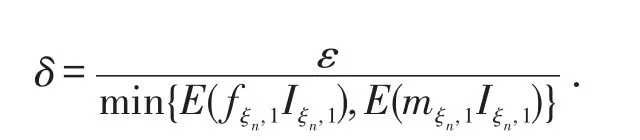
类似可证

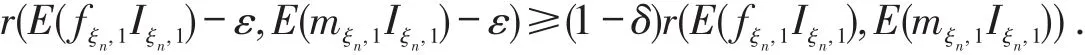
令ε↓0,则δ↓0,可得

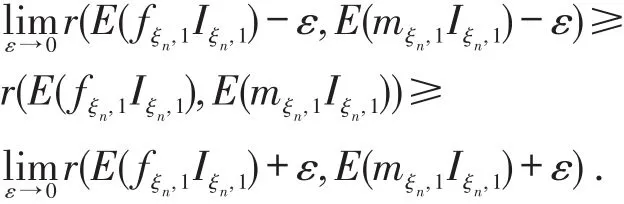
又因为

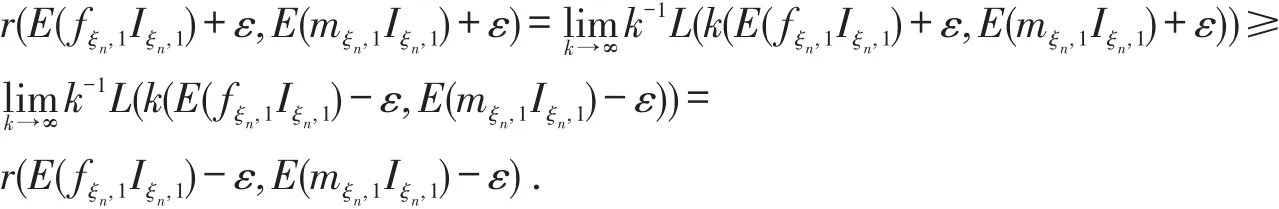
所以有

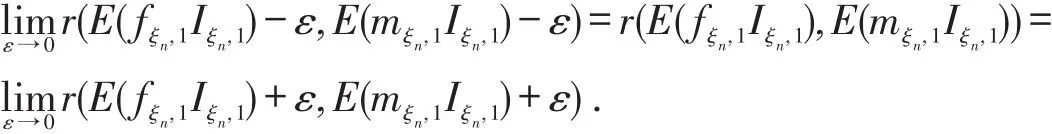
即r(x,y)在D上是二元函数.

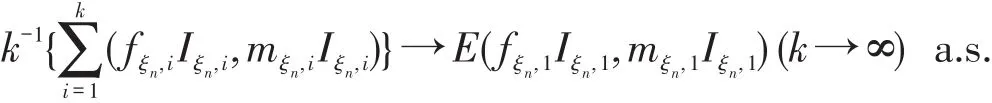
所以，对任意ε,依概率1存在k0∈N，当k≥k0时，有

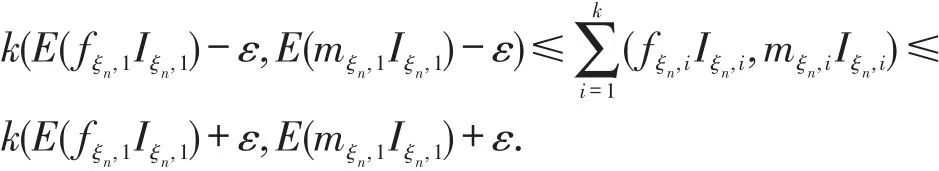
由L(x,y)的单调不减性可得

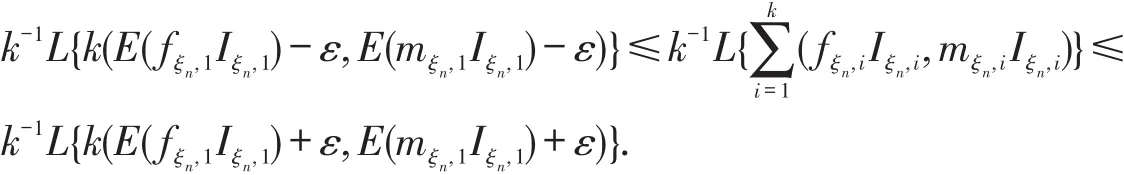
令k→∞有

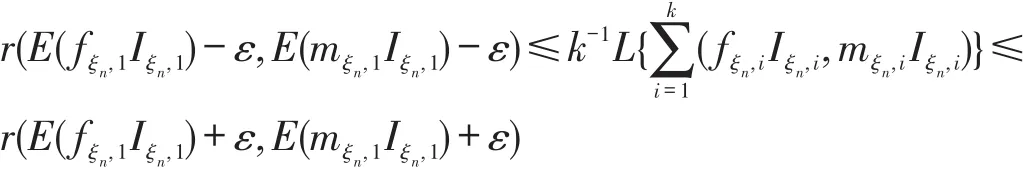
令ε↓0，因为L(x,y)是连续函数，所以有

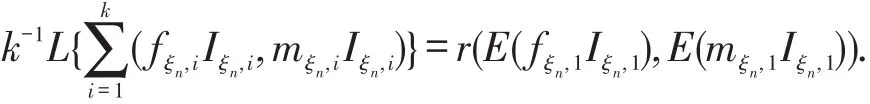
第5步，证明

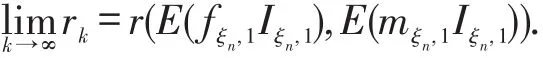
因为L(x,y)≤x+y，所以

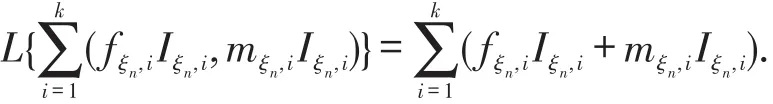
由强大数定律得

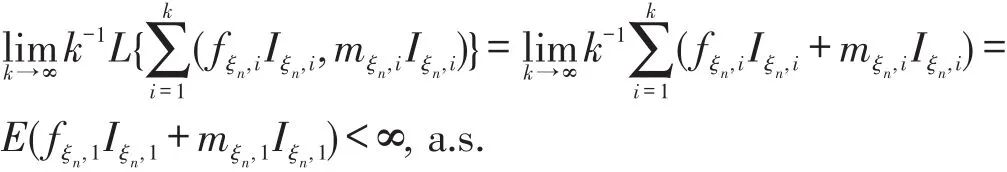
所以当k充分大时，有

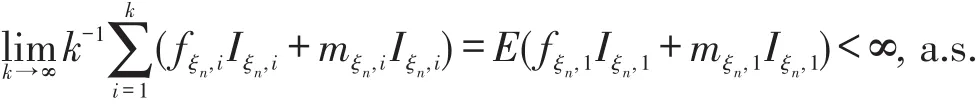
由控制收敛定理可得

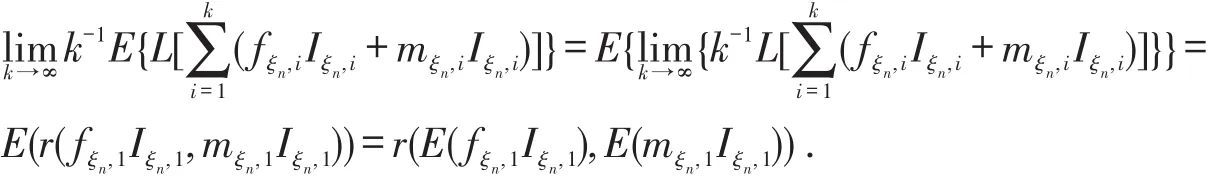
令φk=k∙rk,θ,∀k,j∈N有

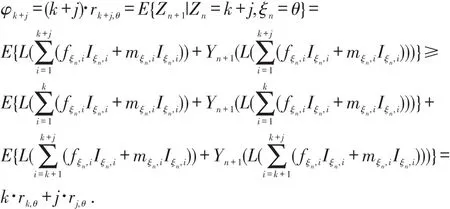
φk是上可加的，故

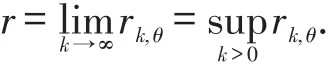
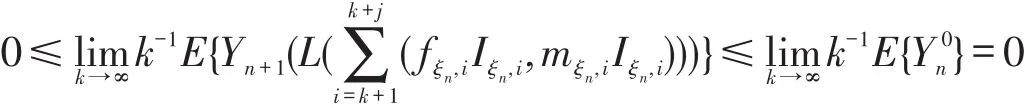
故

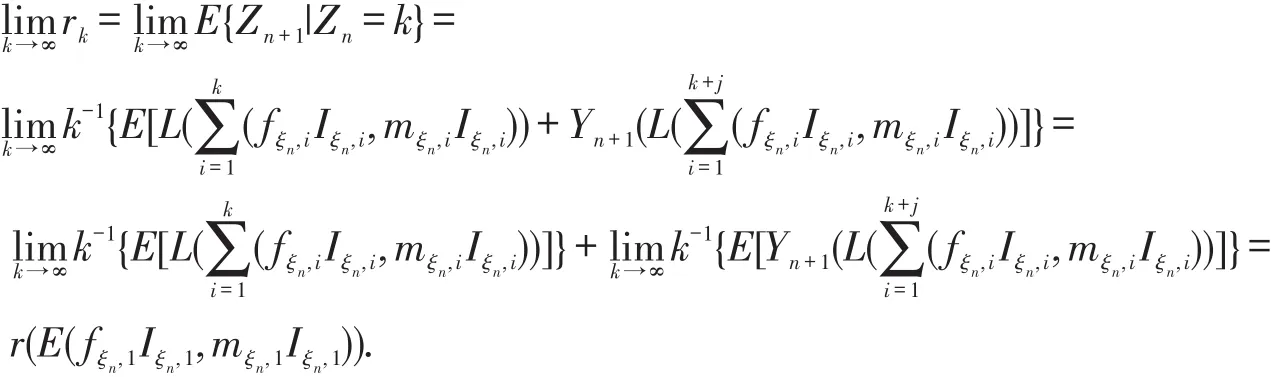
定理2.2 设随机环境是ξ⇀={ξn,n≥0}独立同分布的，配对函数L(x,y)和Yn(∙)是上可加的，则存在非负随机变量W使

证明 对任意的n≥0，由Wn的定义知

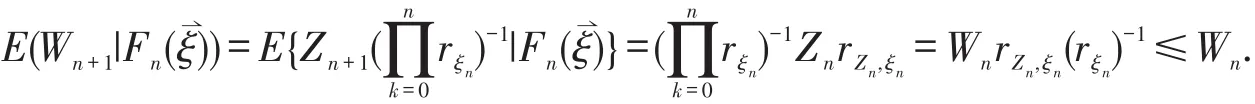
从而Wn是一个非负上鞅，又因为

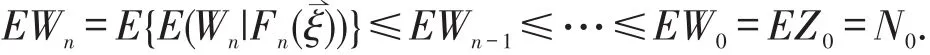
由鞅收敛定理知，存在一个非负有限随机变量W，使得

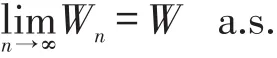
记σk,θ:=k-1Var[Zn+1|Zn=k,ξn=θ],k=1,2,…;n=0,1,2,…,则

设存在序列σξn,n=0,1,2,…,使σk,ξn≤σξn,k=1,2,3,…

定理2.3 设随机环境是 ξ⇀={ξn,n≥0}独立同分布的，配对函数L(x,y)和Yn(∙)是上可加的，若则存在一个非负随机变量W，使得

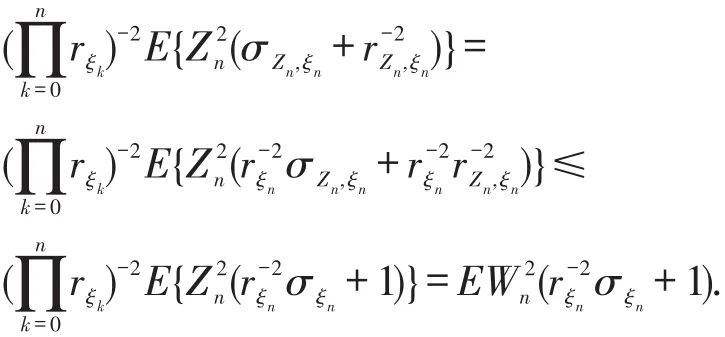
由上式递推可得

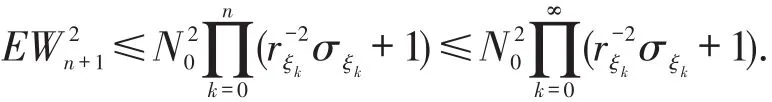
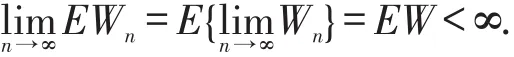
由引理2.1和定理2.3知

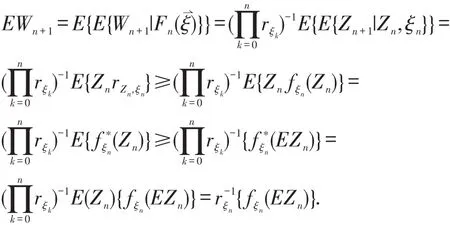
由上式递推可得

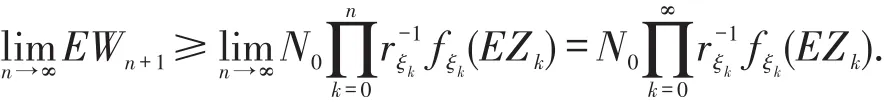
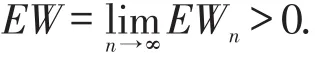
参考文献：

［1］ALSMEYER G，ROSLER U.The bisexual Galton-Waston process with promiscuous mating：Extinction probabilities in the supercitical case［J］.Ann Appl Probab，1996，6：922-939.

［2］DALEY D J.Extinction conditions for certain bisexual Galton-Waston process［J］.Z Wahrscheinlichkeits Theorie Verw Geb，1968，9：315-322.

［3］GONZALEZ M，MOLINA M.On the convergence of a superadditive bisexual Galton-Waston branching process［J］.J Appl Probab，1997，34：575-582.

［4］GONZALEZ M，MOLINA M，MOTA M.Nonparametric estimation of the offspring distribution and the mean vector for a bisexual Galton-Waston process［J］.Comm Statist Theory Methods，2001，30：497-516.

［5］GONZALEZ M，MOLINA M，MOTA M.BisexualGalton-Waston branching processwith immigration of females and males：Asymptotic behaviour［J］.Markov Process Relat Fields，2002，8：651-663.

［6］MOLINA M，MOTA M，RAMOS A.Limit behaviour for a supercritical bisexual Galton-Waston branching process with population-size dependent mating［J］.Stochastic Process Appl，2004，112：309-317.

［7］宋明珠.随机环境中伴有移民两性分枝过程的极限性质［J］.应用数学，2012，25（3）：667-671.

［8］刘宣，张杰华.具配对单元移出的两性分支过程的灭绝性［J］.生物数学学报，2015，30（3）：463-468.

The Limit Properties of the Bisexual Branching Process with Migration of Mating Units in Independent Random Environment

REN Min，ZHANG Guanghui
（School of Mathematics and Statistics，Suzhou University，234000，Suzhou，Anhui，China）

The purpose of this paper is to study the bisexual branching process with population-size-dependent migration of mating units in random environments.The process follows Markov chains in independent and identically distributed random environments.We derive limit properties of the mean growth rate per mating unit.The results extend and improve known results about classical bisexual branching process in random environments.

random environments；bisexual branching process；the mean growth rate；limit properties

O 211.62

A

2095-0691（2017）01-0007-06

2016-12-19

国家自然科学基金面上项目（11371029）；安徽省高校自然科学研究项目（KJ2016A770）；安徽省优秀青年人才支持计划重点项目（gxyqZD2016340）；宿州学院教学研究项目（szxy2015jy09）;宿州学院重点科研项目（2016yzd05）

任 敏（1982- ），女，安徽淮北人，讲师，硕士，研究方向：随机环境中的随机过程.