无人驾驶铰接式车辆强化学习路径跟踪控制算法

邵俊恺 赵 翾,2 杨 珏 张文明 康翌婷 赵鑫鑫

(1.北京科技大学机械工程学院， 北京 100083； 2.北京华为数字技术有限公司， 北京 100085)

无人驾驶铰接式车辆强化学习路径跟踪控制算法

邵俊恺1赵 翾1,2杨 珏1张文明1康翌婷1赵鑫鑫1

(1.北京科技大学机械工程学院， 北京 100083； 2.北京华为数字技术有限公司， 北京 100085)

针对无人驾驶铰接式运输车辆无人驾驶智能控制问题，提出了一种强化学习自适应PID路径跟踪控制算法。首先推导了铰接车的运动学模型，根据该模型建立实际行驶路径与参考路径偏差的模型，以PID控制算法为基础，设计了基于强化学习的自适应PID路径跟踪控制器，该控制器以横向位置偏差、航向角偏差、曲率偏差为输入，以转角控制量为输出，通过强化学习算法对PID参数进行在线自适应整定。最后在实车道路试验中验证了控制器的路径跟踪质量并与传统PID控制结果进行了对比。结果表明，相比于传统PID控制器，强化学习自适应PID控制器能够有效减小超调和震荡，实现精确跟踪参考路径，可以较好地实现系统动态性能和稳态误差性能的优化。

铰接式车辆； 驾驶； 强化学习； 路径跟踪

引言

铰接式车辆作为一种灵活、机动的运输设备，常用于非结构地形运输作业，然而特殊的转向形式使其路径跟踪控制与传统车辆有很大差别。

针对路径跟踪控制算法，国内外众多学者进行了大量研究，主要算法包括比例积分微分(PID)控制[1]、滑模控制[2]、模糊控制[3]和智能控制[4]等。随着被控对象越来越复杂，控制器设计经常结合多种算法来实现功能互补和性能提升。ASLAM等[5]针对滑移转向车动力学模型进行了模糊滑模控制路径跟踪，赵翾等[6]针对铰接式车辆使用Ackermann公式与指数趋近律设计滑模控制进行路径跟踪。TALEBI等[7]提出一种用于轮式机器人的模糊PID路径跟踪控制器，将模糊逻辑用于PID参数调校。文献[5-7]所使用的路径跟踪算法均为离线算法，不能根据使用环境在线优化。裴岩[8]使用强化学习算法对车载导航系统路径规划进行优化，并预测了短时交通流。沈晶等[9]和付成伟[10]提出了一种基于分层强化学习的移动机器人路径规划算法，用于位置动态环境的路径规划。文献[8-10]均使用强化学习算法研究路径规划问题，与路径跟踪问题模型不同。

本文开发一种结合机器学习与PID控制的路径跟踪算法并使用实车道路试验验证控制品质，旨在实现无人驾驶铰接式车辆路径跟踪在线优化。

1 铰接车模型

1.1 铰接车数学模型

铰接车转向过程可以分解为2个运动，即稳态转向运动和原地转向运动，以下分别就这2种运动过程进行分析。

图1 铰接车稳态转向示意图Fig.1 Schematic of articulated vehicle in steady-state steering

图1为铰接车稳态转向模型，其中O为瞬心，Pf(xf,yf)和Pr(xr,yr)分别为前后桥中点，lf和lr分别为前后桥与铰接点距离，θf和θr为前后车体朝向，即航向角，前后车体夹角γ为铰接转向角。出于习惯考虑，通常以铰接车前桥中点Pf为整车状态参考点，因为该点的速度与铰接车的前进方向一致，有利于分析计算[11]。

定义整车速度v为[12]

v=vf

(1)

式中v——整车速度，m/svf——前车架速度，m/s

前桥中点Pf速度[13]为

(2)

式中xf——前桥中点横坐标，myf——前桥中点纵坐标，mθf——前桥航向角，rad

前桥航向角变化率即前桥角速度为

(3)

式中lf、lr——前、后桥与铰接点距离，mγ——铰接转向角，rad

铰接车稳态转向过程前桥的位姿状态可表示为Pf=(xf,yf,θf,γ)，即

(4)

图2为铰接车原地转向模型，因为Pf为整车状态参考点，因此认为原地转向过程中该点相对地面静止[6]。

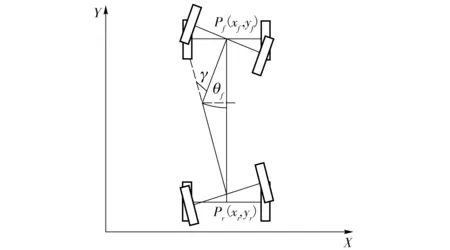
图2 铰接车原地转向示意图Fig.2 Schematic of articulated vehicle in pivot steering

则前桥中点Pf在XY平面上的速度分量为

(5)

航向角变化率为

(6)

铰接车稳态转向过程前桥的位姿状态可表示为Pf=(xf,yf,θf,γ)，即

(7)

联立式(4)、式(7)得出铰接车位姿状态Pf= (xf,yf,θf,γ)，即

(8)

1.2 运动路径描述

图3为铰接车路径示意图，定义了铰接车在行驶过程中，实际路径和参考路径之间的偏差[14-16]。小圆圆心为c，是铰接车瞬时实际行驶轨迹；大圆圆心为C，是铰接车参考轨迹。理想情况下，铰接车应能通过参考轨迹上的3个点P1、P2、P3。

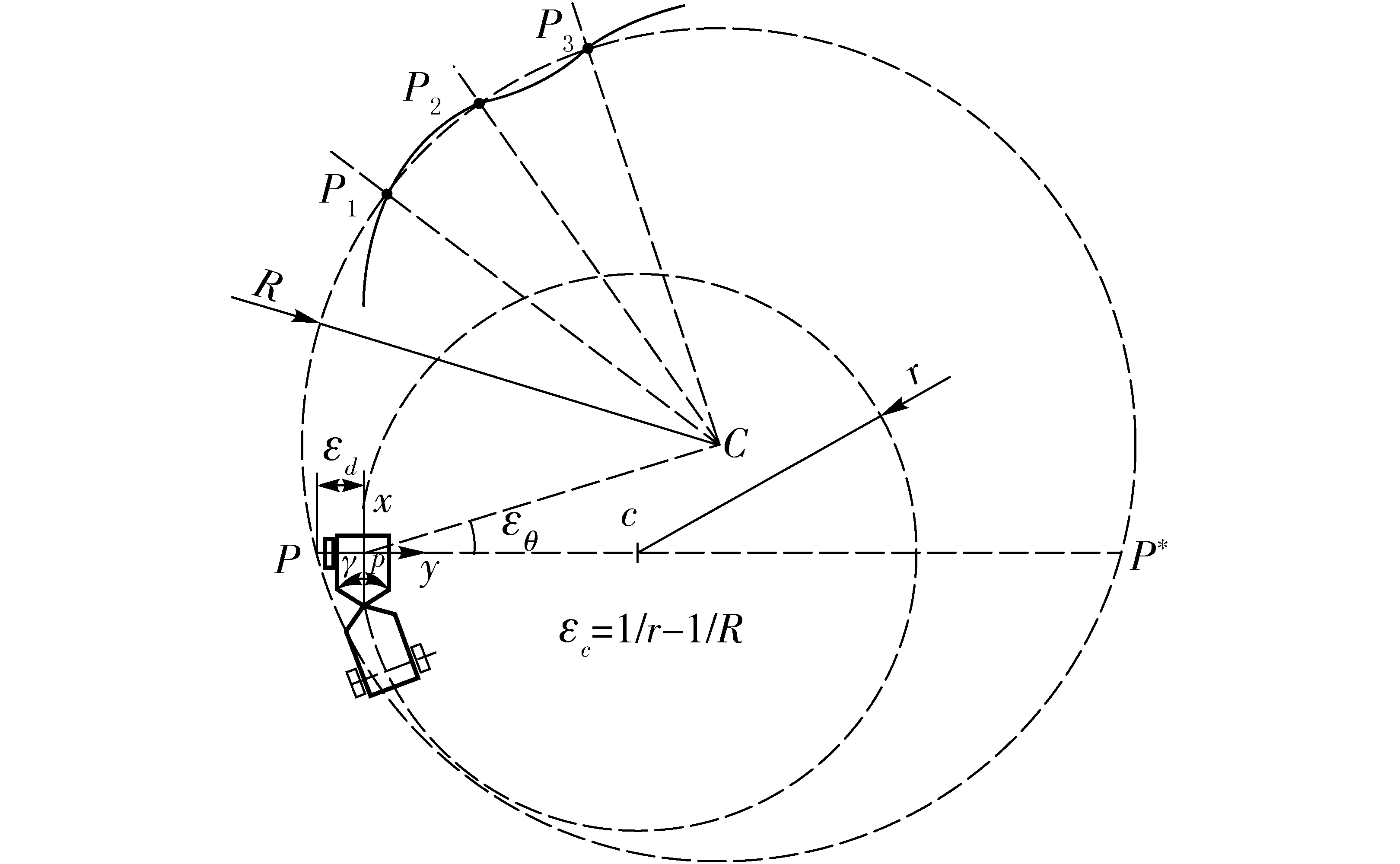
图3 铰接车路径示意图Fig.3 Schematic of articulated vehicle path

现定义如下变量[17-18]：

(1)横向位置偏差εd：铰接车参考定位点p与参考路径上对应点P(与参考路径距离最近点)的横向位置差值。

(2)航向角偏差εθ：铰接车定位参考点p的航向角(速度方向与车辆坐标系X轴之间的夹角)与参考路径上对应点P的航向角(对应点的切线与车辆坐标系X轴之间的夹角)的差值。

(3)曲率偏差εc：铰接车定位参考点p与参考路径上对应点P的曲率差值。

图4为实际路径逼近参考路径情况示意图。图4a为实际路径与参考路径平行的情况，此时两路径距离即为横向位置偏差εd，控制器可以根据该偏差计算控制量使横向位置偏差εd减小；图4b为实际路径与参考路径相交的情况，此时两路径夹角即为航向角偏差εθ，当铰接车向参考路径接近时，虽然减小了横向位置偏差εd，却产生了航向角偏差εθ，在铰接车行驶至路径交点处时横向位置偏差εd消除，但由于车体惯性与外界环境干扰等因素影响，铰接车依旧保持之前的航向，则下一时刻开始横向位置偏差εd再次产生，因此航向角偏差也需要作为控制器输入进行控制；图4c为实际路径与参考路径相切的情况，此时两路径切点处曲率差为曲率偏差εθ，铰接车行驶至切点位置时横向位置偏差εd与航向角偏差εθ均为0，但由于车体惯性与外界环境干扰等因素影响，铰接车依旧保持之前的转角，则下一时刻开始横向位置偏差εd与航向角偏差εθ再次产生。因此横向位置偏差εd、航向角偏差εθ、曲率偏差εc均需要作为控制器输入进行偏差控制，以加快收敛速度、减小震荡。

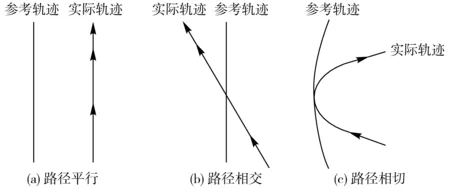
图4 实际路径逼近参考路径情况示意图Fig.4 Schematics of real path and reference path

2 强化学习自适应PID路径跟踪算法

2.1 强化学习方法

强化学习是机器学习中的一种重要方法，不同于监督学习方法，其不需要根据样本进行训练[19-20]，而是通过与外界环境进行互动，并收到环境反馈和评价结果来选择下一时刻执行动作。该算法适合在线优化。因此本文使用强化学习方法对PID参数进行在线实时整定，从而使路径跟踪控制器自适应不同工况。

2.2 强化学习自适应PID算法

强化学习自适应PID算法结构如图5所示[21]，自适应PID控制器为一个可以随输入变化而改变增益的PID控制器，被控对象即铰接车，输出为路径偏差，参考模型则是对偏差收敛的趋势进行规定，以获得理想的收敛效果。参考模型期望的偏差收敛值与实际偏差差值根据回报函数计算会得到一个当前参数效果的评价，通过累计历史回报计算综合回报指标，作为Actor-Critic网络对历史多次参数调整结果的优劣的评价，再根据评价调整新的增益参数，并传递给PID控制器。

则自适应PID控制器的PID增益为

K(t)=K0+ΔK

(9)

式中K(t)——自适应PID增益向量K0——常数向量 ΔK——自适应PID增益可变向量

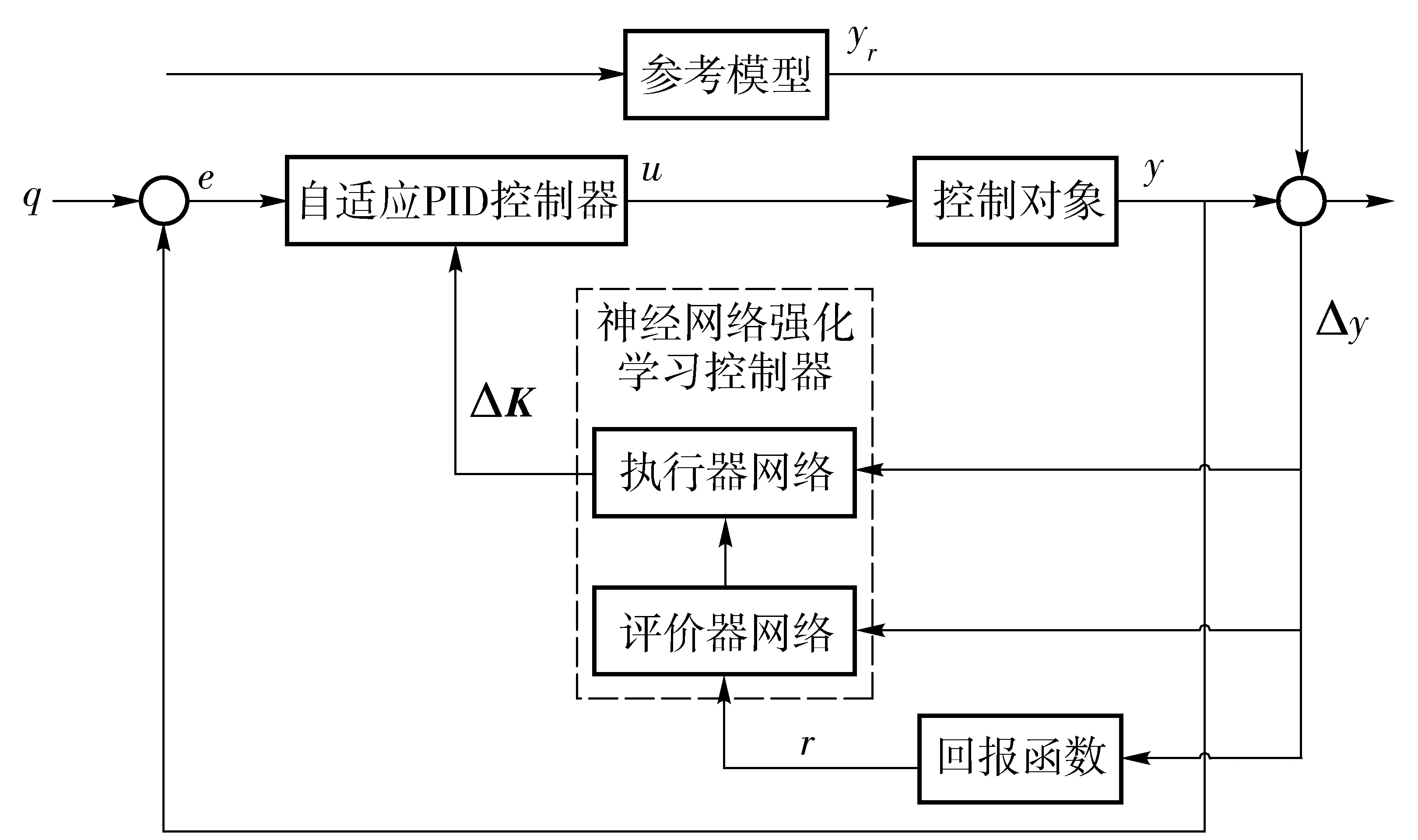
图5 强化学习自适应PID算法结构Fig.5 Flowchart of enforcement learning adaptive PID

由于被控对象输出不是单一变量，Actor-Critic网络根据评价进行随机探索需要指定分布规则，这里选用高斯分布作为动作执行概率的表述[22]，即

(10)

(11)

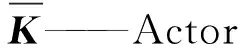
回报函数用于对当前整定的参数效果进行评价，因此直接关系到后续动作的选择，一般以参考模型和被控对象输出差值的加权作为回报函数用以评价参数效果。

rt=k|Δy|

(12)

式中rt——回报值k——比例系数，常数或分段常数

Actor-Critic结构中Critic需要更新历史执行动作的综合评价，因此需要定义指标用来量化综合评价，学习的优化目标是使历史折扣回报最大化，综合回报指标为

(13)

式中J——折扣总回报指标β——折扣因子

由于回报函数输入是实际偏差与参考模型的期望偏差的函数，因此综合汇报指标可以反映实际偏差对参考模型逼近的程度。

强化学习自适应PID控制器学习算法停止准则为综合回报指标达到要求或学习次数达到给定最大值。本文使用的自适应PID算法使用Actor网络输出作为可变增益部分的结果，相比直接作为全部增益结果，避免了初期学习时输出不稳定和学习时间长的问题。

2.3 路径跟踪控制算法设计

根据偏差定义，强化学习自适应PID控制律为

u(t)=(kd0+Δkd)εd(t)+(kθ0+Δkθ)εθ(t)+

(14)

式中kd0、kθ0、kc0、kD、kI——PID增益常数部分 Δkd、Δkθ、Δkc——PID增益可变部分

为了加快学习时间、避免系统不稳定输出，式(9)中PID增益常数部分由试凑得出，而增益可变部分通过强化学习自适应PID控制器调节，从而优化不同工作环境下的路径跟踪性能。

根据式(14)的自适应PID控制律，控制器强化学习部分由Actor-Critic网络组成[23]，参考模型期望的偏差与实际偏差差值作为Critic的输入，Critic输出为当前增益值下的值函数，Actor输入与Critic相同，网络输出则为增益的调节结果。Critic使用CMAC网络，Actor使用BP神经网络。PID增益可变部分采用式(10)进行随机尝试。定义z1、z2、z3(0≤zi≤1，i=1,2,3)为Actor的输出，则可变增益为[24]

(15)

式中Ud、Uθ、Uc——可变增益Δkd、Δkθ、Δkc的变化范围

为了获得理想偏差收敛效果，定义参考模型为

(16)

式中b——正常数

该参考模型定义了系统输出偏差应按照指数收敛，收敛速度可以通过调节系数控制。

作为Critic对Actor输出的评价，回报函数设计为

(17)

式中e1、e2、c——常数k——回报比例系数

其中，0≤e1≤e2，c>0，k>0。该回报函数使系统侧向偏差趋向参考模型偏差，从而达到指数收敛性能。

3 道路试验

铰接车路径跟踪控制试验使用环形模拟巷道进行测试，如图6所示，通过测量各向偏差与控制器输出对控制效果进行验证。

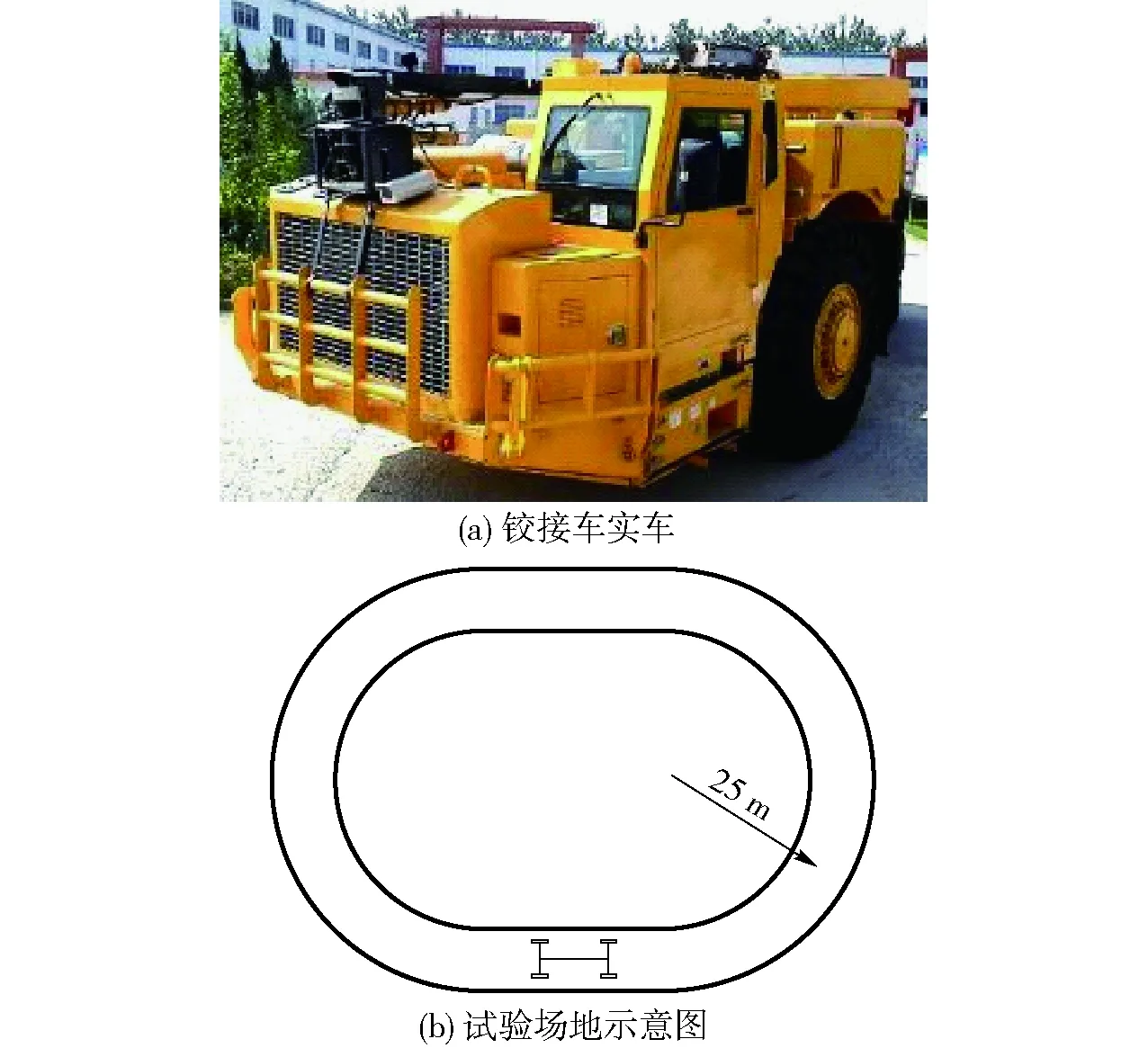
图6 路径跟踪试验Fig.6 Test of path following

利用强化学习算法的自适应PID路径跟踪控制器对铰接车进行路径跟踪，测试环形道路路径跟踪性能。其中参考模型和回报函数参数为：b=0.2，k=0.4，e1=0.05，e2=0.01，c=0.1，Critic网络学习因子为0.05，Actor网络学习因子为0.2。

PID增益由手工试凑得出，其中增益常数部分为kd=80，kθ=45，kc=3，kI=1，kD=0.1。自适应PID控制器增益可变部分为Ud=40，Uθ=30，Uc=4。根据以上参数，分别使用传统固定增益PID控制器和强化学习自适应PID控制器对环形道路进行路径跟踪试验以验证控制器性能，试验时间100 s。

4 试验结果分析

图7和图8分别给出了路径跟踪过程中固定参数PID和强化学习自适应PID控制器的性能比较，包括偏差变化和转向角控制量变化情况。

图7 路径跟踪偏差曲线Fig.7 Changing curves of errors in path following

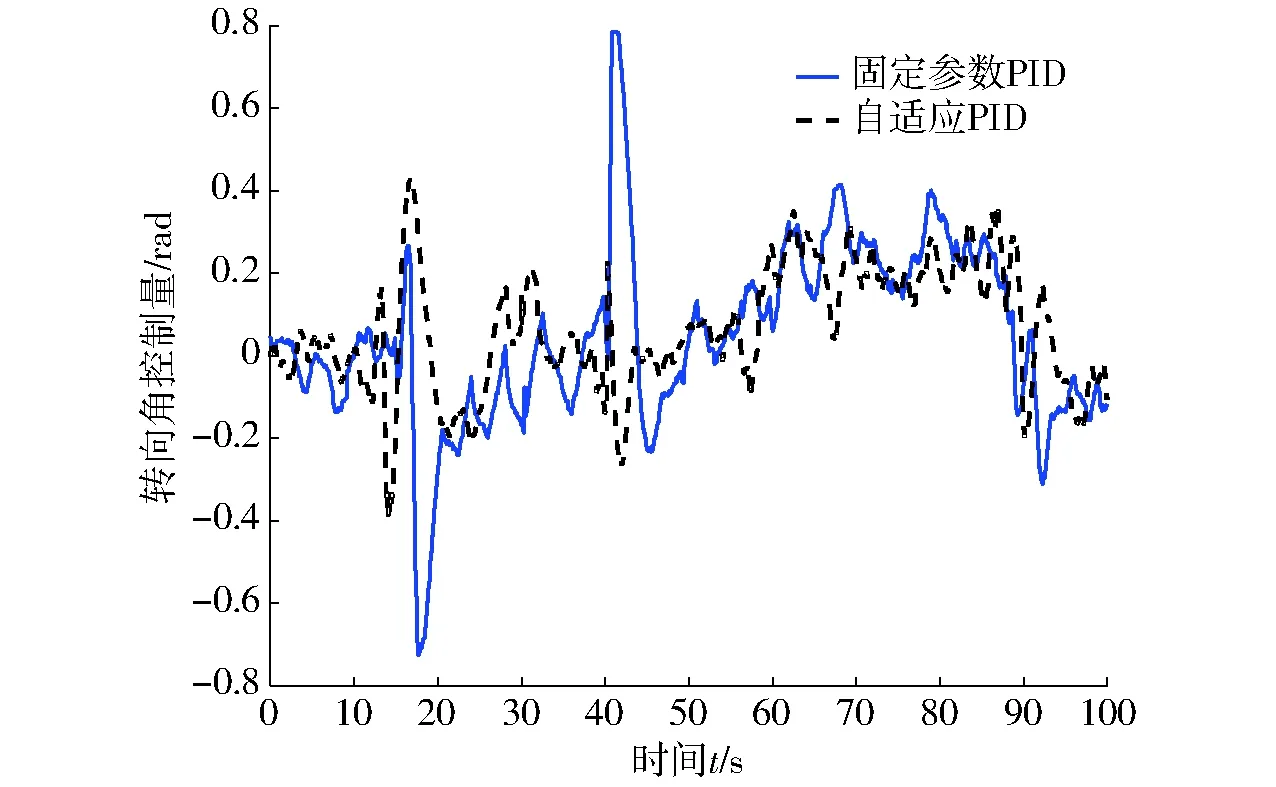
图8 路径跟踪转向角控制量曲线Fig.8 Changing curves of desired articulated angles in path following

表1为试验结果统计，可以看出经过强化学习自适应PID算法相比固定参数PID算法各向偏差和控制量的幅值、均值、方差均有明显减小。表明该算法能有效减少震荡和稳态误差、提高收敛速度。

图9显示了经过强化学习后的自适应PID控制器增益变化情况，横向位置偏差增益系数从初始固定增益80增至90附近，随后在80～100之间调整；航向角偏差增益系数从初始固定增益45迅速降至35，随后在32～38之间调整；曲率偏差增益系数从初始固定增益3迅速降至1.9，随后在1.7～2.1范围内。可以看出偏差增益系数随偏差变化情况进行自适应改变。当实际路径与参考路径距离较远时横向位置偏差影响起主要作用，而当实际路径接近参考路径时，航向角偏差与曲率偏差起主要作用。该算法可以实现PID控制器参数的自适应整定，实现路径跟踪控制的智能化。

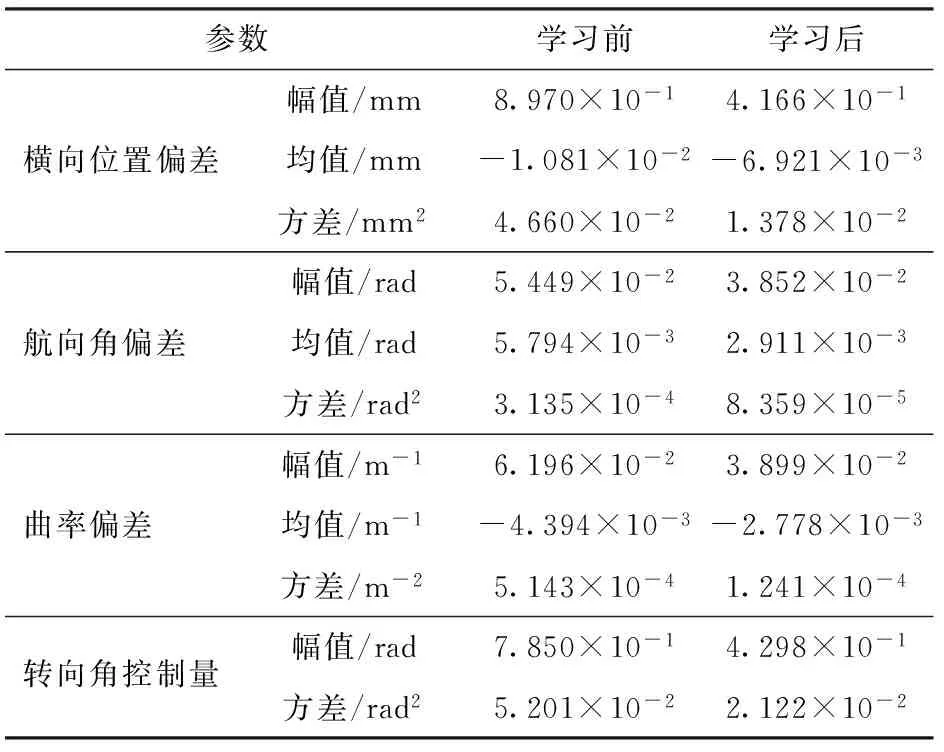
表1 试验结果统计Tab.1 Statistics of test result

图9 路径跟踪比例增益变化Fig.9 Changes of proportional in path following

5 结束语

提供了一种应用于无人驾驶铰接式车辆的强化学习自适应PID控制精确路径跟踪的方法，以横向位置偏差、航向角偏差、曲率偏差作为路径跟踪算法输入，实现了铰接式车辆路径跟踪，试验结果表明，该算法稳定可靠，可以实现铰接式车辆的在线优化路径跟踪控制。横向位置偏差幅值、均值、方差分别为4.166×10-1mm、-6.921×10-3mm、1.378×10-2mm2，航向角偏差幅值、均值、方差分别为3.852×10-2rad、2.911×10-3rad、8.359×10-5rad2，曲率偏差幅值、均值、方差分别为3.899×10-2m-1、-2.778×10-3m-1、1.241×10-4m-2，转向角控制量幅值、方差分别为4.298×10-1rad、2.122×10-2rad2，相比于传统PID控制器，强化学习自适应PID控制器能够使铰接式车辆具有更精确的跟踪参考路径。

1 陶永华, 尹怡欣, 葛芦生. 新型PID控制及其应用[M]. 北京: 机械工业出版社, 1998.

2 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005.

3 林辉. 轮毂电机驱动电动汽车联合制动的模糊自整定PID控制方法研究[D]. 长春: 吉林大学, 2013. LIN Hui. Research on composite ABS control strategy of fuzzy self-adjusting PID for electric-wheel vehicle[D]. Changchun: Jilin University, 2013. (in Chinese)

4 辛斌, 陈杰, 彭志红. 智能优化控制:概述与展望[J/OL]. 自动化学报, 2013, 39(11): 1831-1848. http:∥www.aas.net.cn/CN/abstract/abstract18223.shtml. DOI: 10.3724/SP.J.1004.2013.01831. XIN Bin, CHEN Jie, PENG Zhihong. Intelligent optimized control: overview and prospect[J/OL]. Acta Automatica Sinica, 2013,39(11):1831-1848. (in Chinese)

5 ASLAM J, QIN Shiyin, ALVI M A. Fuzzy sliding mode control algorithm for a four-wheel skid steer vehicle[J]. Journal of Mechanical Science and Technology, 2014, 28(8): 3301-3310.

6 赵翾, 杨珏, 张文明, 等. 农用轮式铰接车辆滑模轨迹跟踪控制算法[J/OL]. 农业工程学报, 2015, 31(10): 198-203. http:∥www.tcsae.org/nygcxb/ch/reader/view_abstract.aspx?flag=1&file_no=20151026&journal_id=nygcxb. DOI:10.11975/j.issn.1002-6819.2015.10.026. ZHAO Xuan, YANG Jue, ZHANG Wenming, et al. Sliding mode control algorithm for path tracking of articulated dump truck[J/OL]. Transactions of the CSAE, 2015, 31(10): 198-203. (in Chinese)

7 TALEBI A H, DEHGHANI T A. Using a fuzzy PID controller for the path following of a car-like mobile robot[C]∥International Conference on Robotics and Mechatronics, ICRoM 2013, 2013: 189-193.

8 裴岩. 机器学习理论研究及其在车载导航系统中的应用[D]. 沈阳: 东北大学, 2009. PEI Yan. Research on the machine learning theory and its application in the vehicle navigation system[D]. Shenyang: Northeastern University, 2009. (in Chinese)

9 沈晶, 顾国昌, 刘海波. 未知动态环境中基于分层强化学习的移动机器人路径规划[J/OL]. 机器人, 2006(5): 544-547. http:∥robot.sia.cn/CN/abstract/abstract12918.shtml. DOI: 10.3321/j.issn:1002-0446.2006.05.017. SHEN Jing, GU Guochang, LIU Haibo. Mobile robot path planning based on hierarchical reinforcement learning in unknown dynamic environment[J/OL]. Robot, 2006(5): 544-547. (in Chinese)

10 付成伟. 基于分层强化学习的移动机器人路径规划[D]. 哈尔滨: 哈尔滨工程大学, 2008. FU Chengwei. Mobile robot path planning based on hierarchical reinforcement learning[D]. Harbin: Harbin Engineering University, 2008. (in Chinese)

11 ZHAO Xuan, YANG Jue, LI Lin, et al. Path tracking control for autonomous underground mining articulated dump truck[J]. EEA-Electrotehnica, Electronica, Automatica, 2015, 63(3): 75-82.

12 李建国,战凯,石峰,等.基于最优轨迹跟踪的地下铲运机无人驾驶技术[J/OL].农业机械学报,2015,46(12):323-328. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20151244&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2015.12.044. LI Jianguo,ZHAN Kai,SHI Feng,et al.Auto-driving technology for underground scraper based on optimal trajectory tracking[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2015,46(12):323-328. (in Chinese)

13 习波波. 具有二自由度铰接车体的轮式越野车辆转向系统研究[D]. 长春: 吉林大学, 2013. XI Bobo. Study on steering system of wheeled off-road vehicle with two degrees of freedom articulated body[D]. Changchun: Jilin University, 2013.(in Chinese)

14 张广庆,朱思洪,李伟华,等.铰接摆杆式大功率拖拉机原地转向仿真与实验[J/OL].农业机械学报,2012,43(10):25-30,18. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20121005&journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2012.10.005. ZHANG Guangqing,ZHU Sihong,LI Weihua,et al. Simulation and experiment of in-situ steering of large wheel tractor with hinge swing link[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2012,43(10):25-30,18. (in Chinese)

15 LEE J H, YOO W S. Predictive control of a vehicle trajectory using a coupled vector with vehicle velocity and sideslip angle[J]. International Journal of Automotive Technology, 2009, 10(2): 211-217.

16 NAYL T, NIKOLAKOPOULOS G, GUSTFSSON T. Switching model predictive control for an articulated vehicle under varying slip angle[C]∥2012 20th Mediterranean Conference on Control and Automation(MED), 2012: 890-895.

17 RIDLEY P, CORKE P. Load haul dump vehicle kinematics and control[J]. ASME Journal of Dynamic Systems, Measurement and Control, 2003, 125(1): 54-59.

18 MAKELA H, LEHTINEN H, RINTANEN K, et al. Navigation system for LHD machines[C]∥Proceedings of the 1995 2nd IFAC Conference on Intelligent Autonomous Vehicles, 1995: 295-300.

19 HEMAMI A, POLOTSKI V. Path tracking control problem formulation of an LHD loader[J]. International Journal of Robotics Research, 1998, 17(2): 193-199.

20 MITCHELL T. 机器学习[M]. 曾华军, 张银奎，译. 北京: 机械工业出版社, 2008.

21 吴军, 徐昕, 王健, 等. 面向多机器人系统的增强学习研究进展综述[J/OL]. 控制与决策, 2011, 26(11): 1601-1610,1615. http:∥kzyjc.alljournals.cn/ch/reader/view_abstract.aspx?file_no=2011-0347&flag=1. DOI:10.13195/j.col.2011.11.4.wuj.014. WU Jun, XU Xin, WANG Jian, et al. Recent advances of reinforcement learning in multi-robot systems: a survey[J/OL]. Control and Decision, 2011, 26(11): 1601-1610, 1615. (in Chinese)

22 徐昕. 增强学习与近似动态规划[M]. 北京: 科学出版社, 2010.

23 LIN C, GEORGE L C S. Reinforcement structure/parameter learning for neural-network-based fuzzy logic control systems[J]. IEEE Transactions on Fuzzy Systems, 1994, 2(1): 46-63.

24 BARTO A G, SUTTON R S, ANDERSON C W. Neuronlike adaptive elements that can solve difficult learning control problems[J]. IEEE Transactions on Systems, Man and Cybernetics, 1983, SMC-13(5): 834-846.

25 徐昕. 增强学习及其在移动机器人导航与控制中的应用研究[D]. 长沙: 国防科学技术大学, 2002. XU Xin. Reinforcement learning and its applications in navigation and control of mobile robots[D]. Changsha: National University of Defense Technology, 2002. (in Chinese)

Reinforcement Learning Algorithm for Path Following Control of Articulated Vehicle

SHAO Junkai1ZHAO Xuan1,2YANG Jue1ZHANG Wenming1KANG Yiting1ZHAO Xinxin1

(1.SchoolofMechanicalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China2.BeijingHuaweiDigitalTechnologiesCo.,Ltd.,Beijing100085,China)

With the industry 4.0 embraced a number of contemporary automation, data exchange and manufacturing technologies, the autonomous driving system is widespread. In order to enable the autonomous driving, path following strategies are essential to maintain the normal work of the vehicles. The articulated frame steering vehicles (ASV) are flexible, efficient and widely implemented in agriculture, mining, construction and forestry sectors due to their high maneuverability. The articulated vehicle usually composes of two units, a tractor and a trailer, which are connected by an articulation joint. However, as the ASV dynamics are significantly different from the conventional vehicles with front wheel steering, the path following controller derived for conventional vehicles is considered not to be applicable for the ASVs. Thus the path following control is challenging the robustness. A path following strategy is proposed for the ASVs on the basis of reinforcement learning adaptive PID algorithm. The kinematic model of the ASV is derived by neglecting the vehicle dynamics. Three measurable errors are defined to indicate the deviation of real path from reference path, i.e., lateral displacement error, orientation error and curvature error. These errors are served as the inputs in order to synthesize the path following controller and the desired steering angle is served as the output of path following controller. Based on the PID algorithm, the reinforcement learning method is selected for optimizing the parameters of PID online to reduce the overshoot and chattering. Furthermore, the prototype test is conducted to evaluate the performance of the proposed control law. The result shows that compared with the traditional PID, reinforcement learning adaptive PID controller can restrain the overshoot and chattering efficiently and follow the reference path accurately.

articulated vehicle; driving; reinforcement learning; path following

10.6041/j.issn.1000-1298.2017.03.048

2016-04-18

2016-09-13

国家高技术研究发展计划(863计划)项目(2011AA060404)和中央高校基本科研业务费专项资金项目(FRF-TP-16-004A1)

邵俊恺(1985—)，男，博士生，主要从事无人驾驶及路径跟踪控制研究，E-mail： shao@ustb.edu.cn

杨珏(1975—)，男，副教授，主要从事非公路车辆设计研究，E-mail： yangjue@ustb.edu.cn

TP273; U463.32+5

A

1000-1298(2017)03-0376-07