面向立木识别的有效K-均值聚类算法研究

王亚雄 康 峰 李文彬 文 剑 郑永军

(1.北京林业大学工学院， 北京 100083； 2.中国农业大学工学院， 北京 100083)

面向立木识别的有效K-均值聚类算法研究

王亚雄1康 峰1李文彬1文 剑1郑永军2

(1.北京林业大学工学院， 北京 100083； 2.中国农业大学工学院， 北京 100083)

针对林区自动对靶施药过程中，当立木生长密集时，获取的点云数据聚类准确率低、效率低的问题，提出优化后的K-均值聚类算法，数据获取方式基于2D激光扫描。针对立木点云信息聚类前需对相关数据进行滤波，提出窗口滤波算法，选取产生混合像素点的树干边缘，提取3次连续扫描的混合像素及其近邻点组成滤波窗口，进行最大阈值滤波，结果显示50次试验中仅有2个混合像素点未被滤除，混合噪声的滤除率高。在K-均值算法优化方面，针对算法需预先确定聚类数和初始聚类中心的不足，提出利用斜率变化确定聚类数的方法，试验对5个不同距离下5组立木分别进行100次测量，结果显示错误测量次数仅为3次，并可在试验前期通过人工方式去除，算法合理有效；对哈夫曼树法确定立木扫描点聚类中心的性能进行了试验分析，3种不同树干分布类型下分别运用随机抽样法和哈夫曼树法进行K-均值聚类，前者平均正确率仅为76.4%，后者则为95.5%；同时分析了Ⅰ型分布下2种算法聚类的迭代次数和耗时，5个不同距离下，随机抽样法的平均迭代次数明显高于哈夫曼树法，平均运行耗时上，哈夫曼树法则高于随机抽样法，前者变化范围为120～220 ms，后者为50～85 ms，该范围为林区测绘的可接受范围。试验证明，基于斜率变化确定聚类数和基于哈夫曼树法确定聚类中心的K-均值算法是林区立木点云聚类的有效算法，可应用于林区的立木检测。

立木识别； 点云数据；K-均值聚类算法； 窗口滤波算法； 哈夫曼树法

引言

林区立木信息的采集与前期处理是林业领域的重要研究内容，如精准对靶施药[1-2]、林木采伐[3]、林业测绘[4]、植株信息分类[5]、森林火灾预测[6]、森林植物地带划分[7]、苗木质量分级[8]等。其中对获取的立木信息如何进行有效聚类是该过程的关键环节，对确定立木的形态与位置信息具有重要意义。聚类是把一个数据对象(或观测)划分成子集的过程，每个子集是一个簇，使得簇中的对象彼此相似[9]。目前立木信息聚类的常用方法主要有毗连点距离法、系统聚类法[10]、区域分割法[11]以及K-均值算法等。毗连点距离法算法简单，仅在数据量较小且分布简单时适用，且对异常点敏感；系统聚类法可根据不同距离类别实现具体聚类要求，并且可生成直观聚类谱系图，但分类过程需人工干预；区域分割法依据概率方法进行树干簇数判定，算法简便可行，但准确性不高，可能导致误判和漏判。相比上述3种算法，K-均值算法作为聚类分析中的经典算法，具有简单、高效、时间复杂度低等特性[12-13]，除了应用于农林业方面[14-15]外，也常用于文档聚类[16]、图像分割[17]等领域。

但K-均值算法同时存在缺点：需要预先确定聚类数和初始聚类中心，且对初始聚类中心敏感，易陷入局部极小。在聚类数的确定方面，周世兵等[18]提出的聚类数法原理较为复杂，运用到树干点云数据分析时时间开销大；王勇等[19]通过样本数据分层得到聚类数搜索范围的上界，并设计聚类有效性指标来评价聚类后类内与类间的相似性程度，从而在聚类数搜索范围内获得最佳聚类数，该方法能够快速、高效地获得最佳聚类数，对数据集聚类效果良好，适用于数据量较大时的聚类分析，但运用于树干点云数据的分簇上耗时较多。在初始聚类中心选取上，当林区立木生长较密集时，常用的随机抽样法由于其随机性而使选取的聚类中心理想情况较少，导致结果不稳定，使算法陷入局部最优。

本研究探索运用K-均值算法对林区二维立木横截面点云进行高效聚类的优化，服务于林区自动对靶施药系统[1]。针对K-均值算法上述的不足，当林区立木生长较密集时对其进行如下优化：提出基于斜率变化的聚类数确定方法；运用哈夫曼树法(Huffman tree method)确定初始聚类中心。此外，在前期数据滤波部分提出窗口滤波算法。对以上优化方案分别进行室内试验验证，以期在可接受的耗时范围内对树干截面点云进行准确滤波及聚类，以便精确确定立木截面形态及位置，从而进行精准施药。

1 优化模型建立

本研究利用二维激光扫描仪获取林区立木信息，获取的点云数据信息量较大，但这些数据并非完全包含有用信息，需首先对数据进行滤波，滤波后得到的数据为包含有用信息的数据集。对该数据集运用优化后的K-均值聚类算法分成不同的簇，继而在分簇后的数据上进行拟合，提取出树干有效定位识别信息。

1.1 林区立木信息的滤波

对获取的立木扫描数据进行聚类处理前，首先需要对点云数据集进行滤波，以消除异常点对聚类精确度的影响，从而可相对准确地获取立木特征(直径和相对中心位置)。二维激光扫描仪获取的数据需要最终保留完全投影于树干上的点。图1所示为滤波前的点云数据图，扫描数据中的噪声点主要由2部分构成：因距离产生的噪声，如区域A，通常为背景障碍物；混合像素产生的噪声，如区域B所示6个扫描点(标号1～6)。混合像素产生机理详见文献[4]，此处不再赘述。本研究主要滤除上述2部分噪声数据，此外，在测试过程中还可能产生环境噪声，一般采用人工方式去除，如选择适宜天气、加装滤光镜等。对于区域A，可通过距离阈值法滤除[20]，而区域B，部分文献运用弦高阈值法[21]滤除，但该方法无法确定两次相邻扫描时刻的关联性，即在连续扫描过程中，某次扫描的返回数据无法与其相邻两次扫描数据进行对比，导致处理结果不理想。

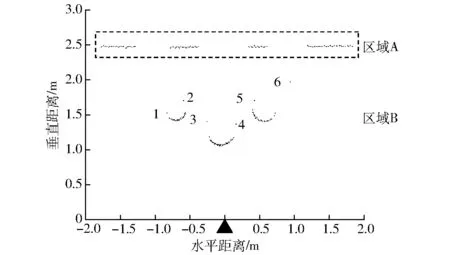
图1 扫描3株树干滤波前的点云Fig.1 Point cloud before filtering when scanning three tree trunks

针对该问题，本文运用一种动态自适应滤波算法对混合像素点进行滤除[22-23]。该方法原理如下： 激光扫描仪对立木数据的采集为连续多次扫描。同一扫描角度上，相邻扫描时刻的测量值具有相关性；同一次扫描中，相邻扫描角度的测量值也具有相关性。对任一距离下测量值ρ和扫描角度λ组成的极坐标(ρi, j，λi, j)建立矩阵窗口

其中i为激光测距的采样编号，即第i次扫描(i为正整数，且i>1)；j为对应某次扫描的不同测量点编号(j为正整数，且j>1)。

以上9个测量值具有时间与空间的最大相关性，在该矩阵窗口中计算ρi,j与邻近测量值之差Δρmin。

Δρmin=min{|ρt+i,s+j-ρi,j|，

t,s=-1,0,1 &t≠0,s=0 &t=0,s≠0}

(1)

当Δρmin>σ(ρ)(σ(ρ)为测量值可接受的邻近差值的阈值，依据实际环境利用不同距离范围下的标准差估计)，测量值ρi,j被视为混合像素测量噪声，对其进行滤除。本文所述试验中σ(ρ)设置为30 mm，依据相邻扫描时刻及扫描角度下相关数据点的距离标准差获取，并预先设定试验使用的距离范围。

1.2 针对林区立木识别的K-均值模型优化

聚类为滤波后进行的数据处理，如图2所示，扫描数据点为完全投影于树干上的点云。对于精准对靶施药而言，首先需对滤波后的点云进行分簇，进而对属于同一树干的点云簇进行拟合。针对所述当前聚类方式的不足，本文根据目标树干的具体情况提出提前确定聚类簇数及初始聚类中心的K-均值算法。

图2 扫描3株树干滤波后的点云Fig.2 Point cloud after filtering when scanning three tree trunks

K-均值算法属于划分聚类算法，其中每个簇的中心都用簇中所有对象的均值来表示。输入为簇的数目(K)与包含n个对象的数据集(D)；输出为K个簇的集合。

算法流程：

(1)从D中任意选择K个对象作为初始聚类中心。

(2)根据簇中对象的均值，将每个对象分配到最相似的簇。

(3)更新簇均值，即重新计算每个簇中对象的均值。

(4)循环步骤(2)、(3)，直到聚类不再发生变化。

提前确定聚类数和初始聚类中心是K-均值聚类法的特点，但在实际林区立木检测中，依靠人工观测确定聚类数目以及随机抽样法确定聚类中心的常规方法费时多且聚类中心确定的正确率低。针对该问题本文提出基于斜率变化确定聚类数的方法，聚类中心的确定则采用哈夫曼树法。

1.2.1 基于斜率变化的聚类数确定方法

本文的研究对象为林区活立木，斜率变化法主要在视野内无遮挡的情况下根据树干上相邻扫描数据点斜率变化的关系得出点云数据的簇数K。如图2所示，各树干上的扫描点云呈弧形均布于面向激光的位置，而相邻两点的斜率逆时针方向必然有从负向正的变化过程，将这样一个过程进行一次数据记录，总的变化数目即为点云数据集的簇数K。

1.2.2 基于哈夫曼树法的聚类中心确定方法

初始聚类中心的选取采用基于哈夫曼树的思想(简称HTM)。HTM简单来说是带权路径长度之和最小的二叉树，也称最优二叉树[24]，主要应用于通信数据编码[25]及图形与文档压缩[26-27]等技术上。算法的构造思想如下：

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。n个权值分别设为w1、w2、…、wn，则哈夫曼树的构造规则为：

(1)将w1、w2、…、wn看成有n棵树的森林(每棵树仅有一个结点)。

(2)在森林中选出两个根结点权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和。

(3)从森林中删除选取的两棵树，并将新树加入森林。

(4)重复步骤(2)、(3)，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

由哈夫曼树带权路径长度之和最小的性质，可将该方法应用于K-均值聚类初始中心的选取上，根结点的合并方法基于对象间的相异性度量，数据间的相异性度量采用相异性矩阵表示。相异性矩阵采用存放n个对象两两之间的邻近度，通常用一个n×n矩阵表示。

其中d(i,j)为对象i、j之间的相异性度量。

一般d(i,j)非负，对象i和j彼此高度相似或“接近”时，其值接近于零；而越不同，该值越大。在本研究中，数据对象为二维数据点，数据间的相异性距离度量采用欧氏距离。

图3 3种不同类型的树干位置分布Fig.3 Three different types of trunks position distribution

根据HTM的思想，基于数据相异度，在本研究中将获取的林区立木数据样本构造成一棵树。为保证数据的近邻性，采用左右结点的算术平均值(本研究中指相邻扫描点的中点)作为新的二叉树根结点的值。然后按构造结点的逆序找到K-1个结点，去掉这K-1个结点可将该树分为K个子树，这K个子树的平均值即初始的K个聚类中心点，对其按照K-均值算法进行聚类。该方法可在理论上获取全局最优解。

2 试验设计与方法

2.1 试验系统

本研究采用德国SICK公司生产的LMS511 20100PRO型激光扫描雷达。在试验中激光扫描雷达作为服务器，客户端为一台Dell E5400型便携式计算机，服务器与客户端之间通过以太网进行通信。该扫描雷达的扫描范围为-5°～185°，试验设置为30°～150°，角分辨率设为0.333°，对应扫描频率为50 Hz。最大探测距离为26 m，本试验设定为10 m。

试验用到的各算法程序加载于版本号为基于哈夫曼树法确定初始聚类中心的林用K-均值算法软件V1.0上[28]，软件在Windows XP环境下基于C/C++语言开发，使用MFC框架。

验证试验在室内进行，树干的分布设置为3种类型，如图3所示，分别为Ⅰ型、Ⅱ型、Ⅲ型分布。其中Ⅰ型分布为距激光扫描仪1、2、3、4、5 m 5个不同距离下对应放置3、3、5、5、7株树干，使其均布于激光扫描仪前，如图3a所示，图中树干中心距激光扫描仪3 m，该分布类型为距离对聚类准确率的定量分析；Ⅱ型、Ⅲ型分布主要验证不同分布类型对聚类准确率的影响，如图3b、3c所示，树干中心距激光扫描仪分别为2.5～3.5 m、1.5～3.5 m。3种分布类型下，树干的直径范围均为50～350 mm。由于传统随机抽样确定初始聚类中心的方法在树干生长较密集时容易导致聚类准确率降低，为检测该情况下基于HTM聚类的准确性，本试验的3种分布类型需确保较小的树间间隔(小于40 mm)。

2.2 滤波试验

首先对立木树干进行连续数据采集找到视野中出现混合像素的树干边缘，测量混合像素及其2个相邻扫描角度返回的距离数据，重复多次(40次以上)并记录获取的距离数值。应用窗口滤波器进行滤波处理，验证滤波效果。

完成混合像素数据滤波后，运用距离阈值法滤去远距离的点云噪声，获得仅属于树干部分的扫描点云。

2.3 聚类分析

首先运用斜率控制法确定树干分簇数目，测量100次，统计簇数确定的正确率，在此基础上分别运用随机抽样法(Random sampling method，RSM)与HTM进行聚类中心的选取。其中，Ⅰ型分布各检测距离下进行3次采样，每次采样的聚类数目(即树干个数)相同，树干直径不同，Ⅱ型、Ⅲ型分布同样进行3次采样，每次采样的聚类数相同(本试验设定为5次)，树干直径不同。运用K-均值算法分别依据2种算法确定的聚类中心对获得的数据点进行分簇，统计采样数据的分簇正确率并比较2种算法的运行时间及迭代次数。考虑到距离变化对结果的影响，运行时间及迭代次数的分析主要针对Ⅰ型分布。

3 结果分析与讨论

3.1 滤波实验结果分析

图4所示为图3中树干B左侧边缘连续测量50次所得混合像素点及相邻两数据点的距离信息统计图。从图中可以得出，当λ为62.33°时，光斑完全投影于树干，返回值为树干与激光扫描仪的距离；当λ为63.00°时，光斑完全投影于背景墙壁，返回值为墙壁与激光扫描仪的距离；当λ为62.67°时，光斑部分投射于背景墙壁，部分投射于树干，返回的距离值界于两者之间。由于每次扫描时激光光斑会有微小差别，因此在50次测量中，混合像素的距离不断变化。运用窗口滤波算法对该像素点进行滤波后，获得图5所示数据，50次滤波中，只有2个数据点未被滤除，原因是2个数据点的距离小于阈值σ(ρ)。通过多次数据统计，该情况出现的概率小于0.5%，当出现运用滤波窗口无法滤去的噪声点时，可配合弦高阈值法将其滤除。试验证明，运用窗口滤波法可有效滤除混合像素点，滤除率大于99.5%，满足林区测绘需求。

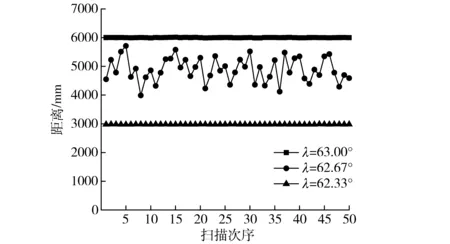
图4 树干B左侧边缘混合像素点滤除前的测距统计Fig.4 Distance statistics of mixed pixels on left edge of trunk B before they were filtered

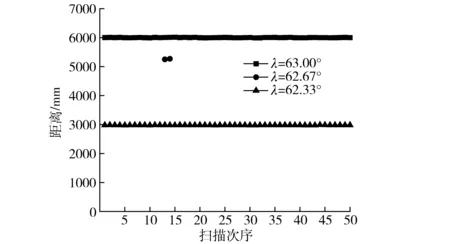
图5 树干B左侧边缘混合像素点滤除后的测距统计Fig.5 Distance statistics of mixed pixels on left edge of trunk B after they were filtered

3.2 聚类试验结果分析

3.2.1 聚类数确定试验结果分析

运用斜率变化法计算树干聚类数目，针对Ⅰ型分布进行，5个不同距离下均测试100次。数据显示仅在距离为2、4 m时分别产生2次和1次错误，原因是这些采样中，由于树干的布置关系，边缘树干在激光扫描视野中仅包含部分信息，导致相邻扫描点斜率正负变化过程的缺失。产生该误差时，只需合理调整激光的视野角度即可。

3.2.2K-均值聚类算法试验结果分析

表1所示为Ⅰ型分布下基于RSM与HTM的K-均值算法对比分析数据，5种不同距离不同聚类数目下RSM样本聚类的平均正确率为72.5%，HTM为95.2%。表2所示为Ⅱ型、Ⅲ型分布下的算法对比分析数据，Ⅱ型分布RSM样本聚类的平均正确率为77.9%，HTM为95.1%；Ⅲ型分布RSM为78.8%，HTM为96.2%。2种算法相比较，基于HTM进行的聚类具有明显优势，平均正确率为95.5%；RSM对初始聚类中心的选取具有一定的随机性，正确选择的概率较小，导致数据的错误归类，平均正确率仅为76.4%。根据表1，RSM聚类的错误率随聚类数目的增加有较明显的增加趋势，符合概率理论。其中采样Y中，2 m处的正确率达到100%是由于该次抽样恰好随机选取了正确的聚类中心。而在本研究中HTM选取聚类中心的原理是基于数据间的欧氏距离分类，聚类中心选取的正确率较高。

提取距离为3 m时采样X的数据样本进行分析，如图6所示。5株树干样本点总量为63，T1～T5为人工聚类的5个簇，即树干样本点的真实聚类结果，与RSM、HTM 2种算法的聚类结果进行对比。T1～T5相对应的样本点数分别为9、13、16、13、12，各簇样本点分别属于5株不同树干，属于不同簇的样本点数量取决于树干直径。T′1～T′5为基于RSM的K-均值聚类结果，对应的样本点数分别为13、14、13、13、10，其中正确聚类的样本个数为50，错误聚类的样本个数为13。对照簇T1～T5，T′1～T′5中错误的聚类样本分别为T′1簇的T′1-1～T′1-4、T′2簇的T′2-1～T′2-5、T′3簇的T′3-1～T′3-2以及T′4簇的T′4-1～T′4-2。T″1～T″5为基于HTM的K-均值聚类结果，对应的样本点数分别为9、13、15、15、11，错误的聚类样本仅为T″4簇的T″4-1和T″4-22个样本点。以上数据说明对于林区立木截面二维扫描点云的聚类，基于HTM的K-均值聚类算法优于基于RSM的K-均值聚类算法。

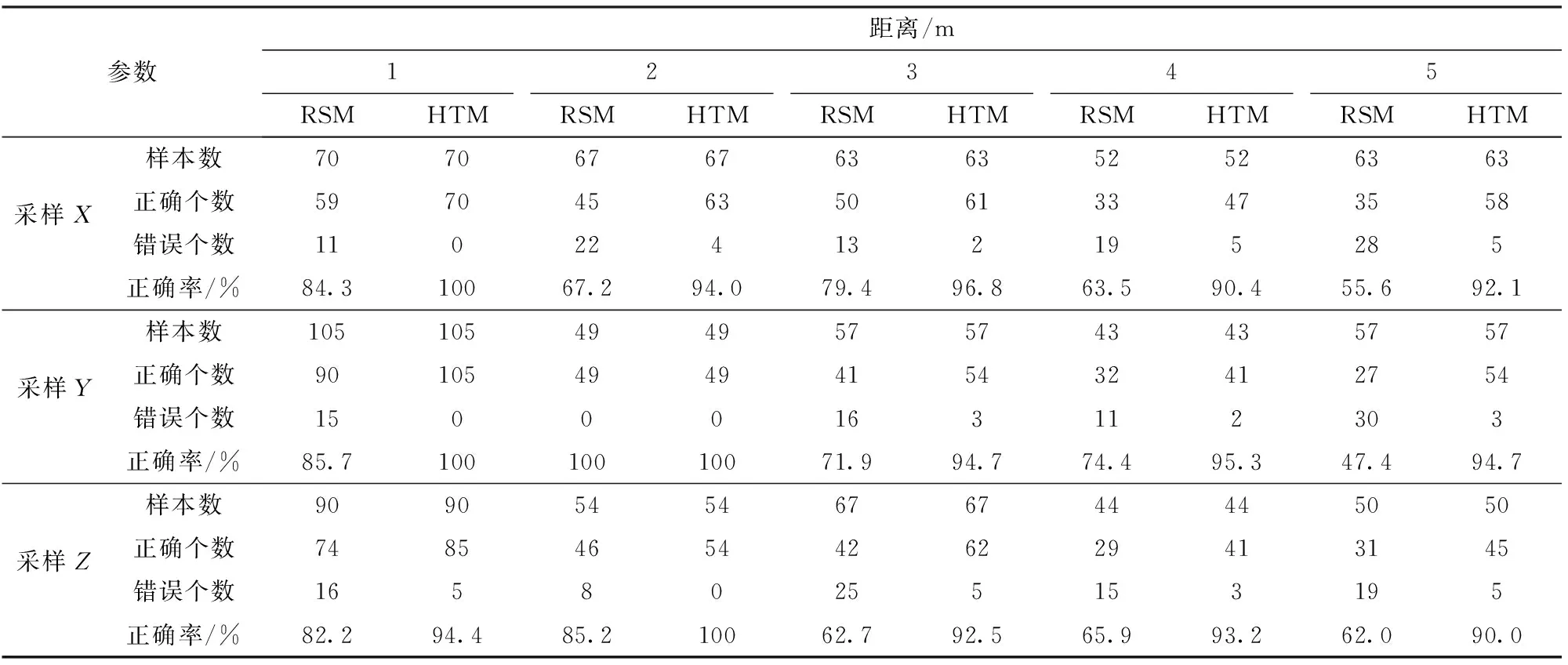
表1 Ⅰ型分布下基于随机抽样法(RSM)与哈夫曼树法(HTM)的K-均值算法对比分析Tab.1 Contrastive analysis of K-means algorithm based on random sampling method (RSM) and Huffman tree method (HTM) at type I distribution

表2 Ⅱ型、Ⅲ型分布下基于随机抽样法(RSM)与哈夫 曼树法(HTM)的K-均值算法对比分析(聚类数5)Tab.2 Contrastive analysis of K-means algorithm based on random sampling method (RSM) and Huffman tree method (HTM) at type Ⅱ and type Ⅲ distributions (five clusters)

图6 距离为3 m时采样X的聚类结果Fig.6 Clustering result of sampling X at distance of 3 m

在Ⅰ型分布下对基于RSM与HTM的K-均值聚类算法进行3次采样并取迭代次数的平均值进行对比分析，如图7所示。图中数据说明，RSM由于选取初始聚类中心的随机性，导致迭代次数的出现也呈随机性，在本试验中，其值为4～8次；而HTM由于初始聚类中心选择的准确性较高，因而运用K-均值算法对样本进行聚类时的迭代次数总体偏少，其值为1～7次，且HTM的迭代次数随聚类数的增加呈递增趋势。

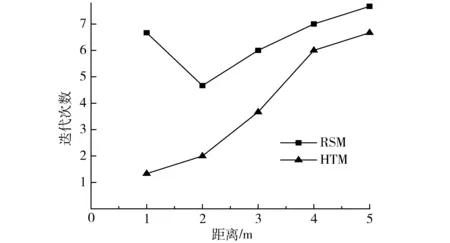
图7 基于RSM与HTM的K-均值算法迭代次数Fig.7 Iterations of K-means algorithm based on RSM and HTM

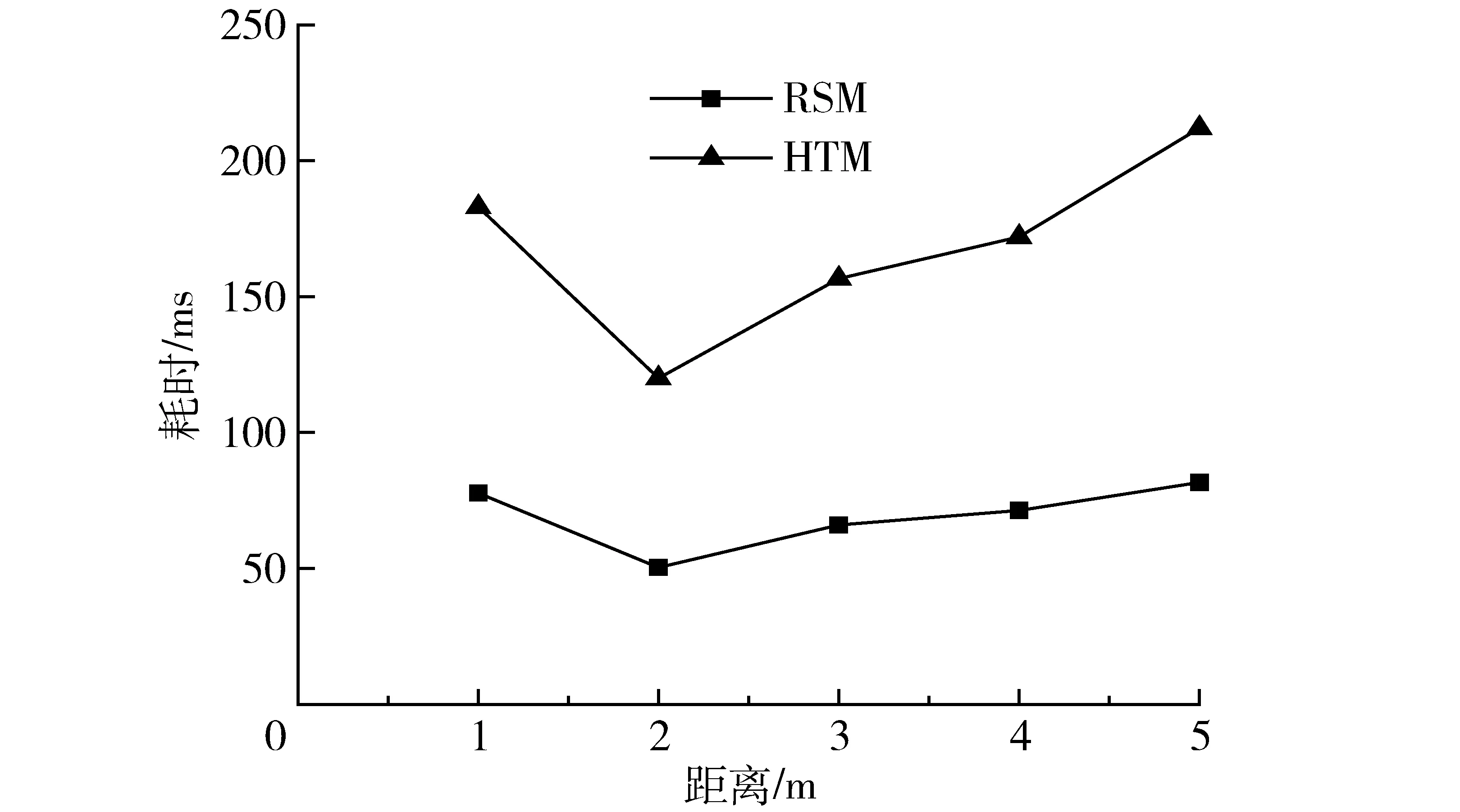
图8 基于RSM与HTM的K-均值算法耗时Fig.8 Time-consuming of K-means algorithm based on RSM and HTM

2种算法的耗时平均值如图8所示(计算机配置：Dell E5400, Intel(R) Core(TM) 2 Duo CPU P8700 @ 2.53 GHz, 3.45 GB RAM)，基于RSM的K-均值算法耗时明显低于HTM，前者为50～85 ms，后者为120～220 ms。由2种算法的原理可知，HTM初始聚类中心选取的耗时大于RSM，而基于RSM的K-均值聚类迭代耗时却大于HTM，前者的差值大于后者，因而对2种算法总的耗时进行对比时，HTM

明显大于RSM。另外迭代次数与耗时还与样本数量相关，由于林区环境下激光扫描仪可识别的最远距离范围内样本数量相对较少，HTM的耗时在林区测绘可接受的数值范围内，因而本文暂不分析样本数量与聚类数目对迭代次数与耗时的影响。

4 结束语

主要分析了林区立木生长较密集时，基于二维激光扫描的有效信息聚类方法，即基于HTM确定初始聚类中心和基于斜率变化确定聚类数的K-均值聚类算法。对激光扫描仪获取的原始数据采用窗口滤波算法对异常点进行了有效滤除，滤除率大于99.5%，进而对比分析了HTM与RSM对初始聚类中心选取的有效性，同时分析了基于2种算法的迭代次数与耗时。分析结果显示，基于斜率变化法确定聚类数的正确率接近100%，基于HTM的K-均值聚类正确率高于95%，而基于RSM的聚类正确率不足80%。基于HTM的K-均值聚类迭代次数较少，但是耗时较高，在本研究Ⅰ型分布的3次采样中，数据样本介于40～100之间，5种距离下平均耗时介于120～220 ms之间，属于林区数据采集可接受的耗时范围。可以得出基于斜率变化确定聚类数与基于HTM确定初始聚类中心的K-均值法为林区立木点云聚类分析的一种有效算法，可应用于林区自动对靶施药系统及林业测绘等领域。

1 KANG F, PIERCE F J, WALSH D B, et al. An automated trailer sprayer system for targeted control of cutworm in vineyards [J]. Transactions of the ASABE, 2012, 55(5): 2007-2014.

2 姜红花，白鹏，刘理民，等. 履带自走式果园自动对靶风送喷雾机研究[J/OL].农业机械学报，2016，47(增刊)：189-195.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=2016s029&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.S0.029. JIANG Honghua, BAI Peng, LIU Limin, et al. Caterpillar self-propelled and air-assisted orchard sprayer with automatic target spray system [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(Supp.): 189-195. (in Chinese)

3 ZHENG Y L, LIU J H, WANG D, et al. Laser scanning measurements on trees for logging harvesting operations [J]. Sensors, 2012, 12(7): 9273-9285.

4 王亚雄，康峰，李文彬，等. 基于2D激光探测的立木胸径几何算法优化[J/OL].农业机械学报，2016，47(6)：290-296. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160638&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.06.038. WANG Yaxiong, KANG Feng, LI Wenbin, et al. Optimization of geometry algorithm for DBH of standing tree on 2D laser detection [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 290-296. (in Chinese)

5 屈洋，周瑜，王钊，等. 苦荞产区种质资源遗传多样性和遗传结构分析[J].中国农业科学，2016，49(11)：2049-2062. QU Yang, ZHOU Yu, WANG Zhao, et al. Analysis of genetic diversity and structure of tartary buckwheat resources from production regions [J]. Scientia Agricultura Sinica, 2016, 49(11): 2049-2062. (in Chinese)

6 梁俊山，王慧琴，胡燕，等. 基于模糊聚类的图像型火灾检测[J].计算机工程，2012，38(4)：196-198. LIANG Junshan, WANG Huiqin, HU Yan, et al. Image type fire detection based on fuzzy clustering [J]. Computer Engineering, 2012, 38(4): 196-198. (in Chinese)

7 姚雪芹，张钦弟，毕润成，等. 山西太岳山辽东栎群落林下草本植物功能群分类[J].植物分类与资源学报，2015，37(6)：849-855. YAO Xueqin, ZHANG Qindi, BI Runcheng, et al. Plant functional group classification of herbaceous species inQuercuswutaishanicacommunities in the Taiyue mountains, Shanxi Province of China [J]. Plant Diversity and Resources, 2015, 37(6): 849-855. (in Chinese)

8 蒋冬生，唐红莲，覃宏明，等. 桂北地区银杏苗木质量分级标准[J].林业科技，2015，40(4)：29-32. JIANG Dongsheng, TANG Honglian, Qin Hongming, et al. Grading standard ofGinkgobiloba. seedling quality in the northern area of Guangxi [J]. Forestry Science & Technology, 2015, 40(4): 29-32. (in Chinese)

9 韩家炜，Micheline K, 裴健. 数据挖掘概念与技术[M].3版.北京：机械工业出版社，2014：288-319.

10 王典，刘晋浩，王建利. 基于系统聚类的林地内采育目标识别与分类[J].农业工程学报，2011，27(12)：173-177. WANG Dian, LIU Jinhao, WANG Jianli. Identification and classification of scanned target in forest based on hierarchical cluster [J]. Transactions of the CSAE, 2011, 27(12): 173-177. (in Chinese)

11 周俊，胡晨. 密植果园作业机器人行间定位方法[J/OL].农业机械学报，2015，46(11)：22-28. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20151104&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.11.004. ZHOU Jun, HU Chen. Inter-row localization method for agricultural robot working in close planting orchard[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(11): 22-28. (in Chinese)

12 LLOYD S P. Least squares quantization in PCM [J]. IEEE Transactions on Information Theory, 1982, 28(2): 128-137.

13 MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]∥Proceedings of the 5th Berkeley Symposium on Mathematical Statistics & Probability, 1967: 281-297.

14 赵博，宋正河，毛文华，等. 基于PSO与K-均值算法的农业超绿图像分割方法[J].农业机械学报，2009，40(8)：166-169. ZHAO Bo, SONG Zhenghe, MAO Wenhua, et al. Agriculture extra-green image segmentation based on particle swarm optimization andK-means clustering [J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(8): 166-169. (in Chinese)

15 司永胜，刘刚，高瑞. 基于K-均值聚类的绿色苹果识别技术[J].农业机械学报，2009，40(增刊)：100-104. SI Yongsheng, LIU Gang, GAO Rui. Segmentation algorithm for green apples recognition based onK-means algorithm [J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(Supp.): 100-104. (in Chinese)

16 KRISHNA K, ROHIT L, SHOURYA R, et al. A hierarchical monothetic document clustering algorithm for summarization and browsing search results [C]∥Proceedings of the 13th International Conference on WWW, 2004: 658-665.

17 LUO M, MA Y F, ZHANG H J. A spatial constrainedK-means approach to image segmentation[C]∥Proceedings of the 4th IEEE Pacific-Rim Conference on Multimedia, 2003: 738-742.

18 周世兵，徐振源，唐旭清. 一种基于近邻传播算法的最佳聚类数确定方法[J].控制与决策，2011，26(8)：1147-1157. ZHOU Shibing, XU Zhenyuan, TANG Xuqing. Method for determining optimal number of clusters based on affinity propagation clustering [J]. Control and Decision, 2011, 26(8): 1147-1157. (in Chinese)

19 王勇，唐靖，饶勤菲，等. 高效率的K-means最佳聚类数确定算法[J].计算机应用，2014，34(5)：1331-1335. WANG Yong, TANG Jing, RAO Qinfei, et al. High efficientK-means algorithm for determining optimal number of clusters [J]. Journal of Computer Applications, 2014, 34(5): 1331-1335. (in Chinese)

20 KANG F, LI W B, PIERCE F J, et al. Investigation and improvement of targeted barrier application for cutworm control in vineyards [J]. Transactions of the ASABE, 2014, 57(2): 381-389.

21 王建，姚振强，尹明德，等. 用于距离图像2D扫描线的极速边缘检测器[J].电子学报，2010，38(7)：1711-1715. WANG Jian, YAO Zhenqiang, YIN Mingde, et al. A rapid edge detector for 2D scan line in range image [J]. Acta Electronica Sinica, 2010, 38(7): 1711-1715. (in Chinese)

22 RODRIGUEZ-CABALLERO E, AFANA A, CHAMIZO S, et al. A new adaptive method to filter terrestrial laser scanner point clouds using morphological filters and spectral information to conserve surface micro-topography[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 117: 141-148.

23 于金霞，蔡自兴，邹小兵，等. 基于动态自适应滤波的移动机器人障碍检测[J].自然科学进展，2006，16(5)：618-624. YU Jinxia, CAI Zixing, ZOU Xiaobing, et al. Obstacle detection of mobile robot based on dynamic adaptive filtering [J]. Progress in Natural Science, 2006, 16(5): 618-624. (in Chinese)

24 CHAUDHURI D, CHAUDHURI B B. A novel multiseed nonhierarchical data clustering technique[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 1997, 27(5): 871-876.

25 熊军华，王彩玲，贠超. 自动配料远程监控系统设计[J].农机化研究，2011(9)：128-131. XIONG Junhua, WANG Cailing, YUN Chao. Design of remote monitoring system of automatic batching[J]. Journal of Agricultural Mechanization Research, 2011(9): 128-131. (in Chinese)

26 张翔，张青峰，张莉，等. 利用哈夫曼树的遥感影像无损压缩方法[J].测绘科学，2015，40(4)：106-111. ZHANG Xiang, ZHANG Qingfeng, ZHANG Li, et al. Huffman tree based lossless compression method for remote sensing image [J]. Science of Surveying and Mapping, 2015, 40(4): 106-111. (in Chinese)

27 特日跟，江晟，李雄飞，等. 基于整数数据的文档压缩编码方案[J].吉林大学学报：工学版，2016，46(1)：228-234. TE Rigen, JIANG Sheng, LI Xiongfei, et al. Document compression scheme based on integer date[J]. Journal of Jilin University: Engineering and Technology Edition, 2016, 46(1): 228-234. (in Chinese)

28 北京林业大学. 基于哈夫曼树法确定初始聚类中心的林用K-均值算法软件V1.0：中国，2016SR250805[P]. 2016-06-29.

EffectiveK-means Clustering Algorithm for Tree Trunk Identification

WANG Yaxiong1KANG Feng1LI Wenbin1WEN Jian1ZHENG Yongjun2

(1.SchoolofTechnology,BeijingForestryUniversity,Beijing100083,China2.CollegeofEngineering,ChinaAgriculturalUniversity,Beijing100083,China)

In the process of automatic targeted spray in forest region at present, the accuracy and efficiency of point cloud data are all low when the tree trunks grow intensively, aimed at which the optimizedK-means clustering algorithm was put forward, and data acquisition method was based on 2D laser detection. In view of the relevant data needed to be filtered before clustering analysis for trunk scanning spots, application of window filtering algorithm was put forward. The edge of trunk which generated mixed pixels was selected, and then the mixed pixels deriving from three adjacent scans and the scanning spots deriving from two scanning angles near the mixed pixel were extracted, finally, the maximum threshold filtering processing for the neighbor spots was done. Through 50 times of extractions and analyses of test data, only two mixed pixels were not filtered, which indicated that the filtering rate of mixed noises was high. Aimed at the defects of cluster number and initial cluster centers forK-means algorithm needed to be predetermined, the method of slope variation used to determine the clustering number was firstly proposed. Five groups of trunks were respectively measured for 100 times at five different distances in the test, and results showed that the number of error measurements was only three times, which could be removed by artificial way at the early stage of the test, and it indicated that the slope variation algorithm was reasonable and effective. The performance of Huffman tree method, which was used to determine the clustering centers for the trunk scanning spots, was analyzed in another test, andK-means clustering was carried out by using random sampling method and Huffman tree method under three trunk distribution types. The average correct rate of former was only 76.4%, while that of the latter was 95.5%. Meanwhile, iterations and time-consuming using the two above-mentioned algorithms at type I distribution were analyzed, and the average number of iterations of random sampling method was obviously higher than that of Huffman tree method at five different distances, but the average time-consuming of Huffman tree method was higher than that of random sampling method. The variation range of former was 120～220 ms and it was 50～85 ms for the latter, which were all in acceptable ranges on forest surveying and mapping. Experiments proved that the determining methods for clustering number based on the slope variation algorithm and clustering centers based on Huffman tree method were effective algorithms for the clustering of trunk scanning spots in forest region during usingK-means algorithm, which could be applied to tree trunk detection for actual forest region.

tree trunk identification; point cloud data;K-means clustering algorithm; window filtering algorithm; Huffman tree method

10.6041/j.issn.1000-1298.2017.03.029

2016-11-15

2016-12-22

国家林业局林业科学技术推广项目(2016-29)和中央高校基本科研业务费专项资金项目(2015ZCQ-GX-01)

王亚雄(1986—)，男，博士生，主要从事林业工程装备及其自动化研究，E-mail： yaxiongwang87@bjfu.edu.cn

李文彬(1962—)，男，教授，博士生导师，主要从事林业工程装备自动化及人工环境工程研究，E-mail： leewb@bjfu.edu.cn

S24

A

1000-1298(2017)03-0230-08