基于高光谱数据的土壤有机质含量反演模型比较

叶 勤 姜雪芹 李西灿 林 怡

(1.同济大学测绘与地理信息学院， 上海 200092； 2.山东农业大学信息科学与工程学院， 泰安 271018)

基于高光谱数据的土壤有机质含量反演模型比较

叶 勤1姜雪芹1李西灿2林 怡1

(1.同济大学测绘与地理信息学院， 上海 200092； 2.山东农业大学信息科学与工程学院， 泰安 271018)

以土壤多样化的陕西省横山县为研究区域，比较了3种基于高光谱数据的土壤有机质含量反演模型，在实验室利用ASD Field Spec FR地物光谱仪对横山县野外采集的土壤样品进行光谱测定，并通过重铬酸钾氧化容量法测定土壤有机质含量。然后对原始光谱反射率的倒数进行微分运算获得其一阶导数光谱，将原始光谱反射率、一阶导数光谱分别与土壤有机质含量进行相关性分析，得到相关性系数r较高的特征波段的一阶导数光谱，直接建立基于一阶导数光谱的多元线性逐步回归分析(MLSR)模型。同时针对这些相关性系数较高的特征波段的一阶导数光谱进行主成分分析(Principal component analysis, PCA)，利用主成分分析得到的结果分别建立BP神经网络反演模型(PCA-BP)和多元线性逐步回归分析模型(PCA-MLSR)。用上述3种方法进行土壤有机质含量反演，并对3种反演结果进行精度验证与比较。实验分析结果表明：在3种模型中，基于主成分分析结果构建的PCA-BP模型在土壤有机质含量反演中决定系数(R2)最高，为0.893 0，均方根误差(RMSE)为0.118 5%；其次为运用全部主成分PCA分析结果构建的多元线性逐步回归模型，R2为0.740 7，RMSE为0.161 3%；而采用一阶导数光谱反射率构建的多元线性逐步回归模型中，最佳反演模型R2仅为0.689 9，RMSE为0.171 0%。由此说明，PCA-BP模型有机质含量反演精度明显高于多元线性逐步回归模型，利用全部主成分进行多元逐步回归，其有机质含量反演精度优于仅用累计方差贡献率大于90%的主成分进行多元逐步回归的精度，可以更好地反演土壤有机质的含量。

土壤； 有机质含量； 一阶导数光谱； 主成分分析； BP神经网络； 多元线性逐步回归

引言

土壤有机质(Soil organic matter，SOM)是指土壤中的所有含碳的有机物质。土壤有机质具有改良土壤结构、疏松土壤的作用，是评价土壤肥沃程度的一个重要指标[1-2]。传统的土壤有机质含量测定方法是通过野外采集数据，并在室内运用化学方法测定。此法耗时长、工作量大且多为点状信息数据，因此不能快速、无损地进行大面积的土壤有机质含量测定[3-4]。土壤光谱反射率与有机质含量之间存在一定的光谱响应关系，这为利用遥感技术进行大面积土壤有机质含量测定提供了依据，现阶段卫星遥感高光谱技术的发展为大面积土壤有机质含量的快速、准确监测提供了一种可能[5-9]。

国内外学者利用高光谱技术对土壤有机质含量估测进行了许多有益研究[10-11]。在土壤反射光谱与有机质含量的相关性方面，发现土壤中有机质含量越高，其光谱反射率越低[12-13]。此外，徐明星等[14]发现可见光波段以1 400 nm为中心及红外波段是估计土壤有机质含量的最佳波段。在利用光谱反射率数据进行土壤有机质含量反演的模型方面，大多是运用最小二乘回归和多元逐步回归的方法[15]。其中侯艳军等[16]、于雷等[17]用不同的方法建立偏最小二乘法回归模型，取得了较好的反演效果。HUMMEL等[18]分析了有机质与近红外光谱的关系，建立了多元逐步回归的反演模型。于士凯等[19]利用光谱一阶微分建立的多元回归模型，决定系数R2达到0.909，具有较高的反演精度。然而因有机质的组成比较复杂，大量文献表明有机质含量反演中决定系数R2能得到的较好结果为0.9左右。VASQUES等[20]综合比较常用的3种分析方法，发现偏最小二乘回归模型较另外两种模型反演效果更好。但上述模型均有反演因子之间共线性大以及样本少的缺陷。杨扬等[21]、栾福明等[22]分别利用人工神经网络以及集成模型反演土壤有机质含量，整体精度高于最小二乘回归模型，但其针对的是有机质含量低的干旱土壤，对有机质含量较高土壤的效果还未知。

已有这些研究多通过相关性分析寻找最佳特征波段，运用多元逐步回归或最小二乘回归构建土壤有机质含量反演模型。但这2种方法对处理土壤有机质反演这样较复杂的非线性问题存在较大估测误差。而BP神经网络(Back propagation neural network)具有较强的非线性处理能力，可以较好地处理土壤有机质含量反演等非线性问题。此外现有方法在利用光谱信息进行反演时，对波段间的相关性分析考虑较少，而这种相关性对反演会产生较大影响。因此，本文先进行光谱变换得到倒数的一阶微分光谱，即一阶导数光谱，并建立基于一阶导数光谱的多元回归模型。同时也对挑选出的最佳特征波段进行主成分分析，再结合多元逐步回归法和BP神经网络建立土壤有机质含量反演模型，并对3种方法进行比较，得到更有效的土壤有机质含量反演方法，以期为利用遥感高光谱影像进行土壤有机质含量的反演及动态变化监测奠定基础。

1 材料与方法

1.1 研究区概况

研究区为陕西省北部的横山县，在北纬37°22′～38°14′、东经109°14′～110°20′之间，位于毛乌素沙漠南缘，处陕北黄土高原、风沙高原过渡区，地势西南高、东北低，总土地面积4 333 km2。北部地形平坦，土质松软，地下水位高，属于风沙和黄土相间的地貌；南部地形支离破碎，沟壑交错，表层为厚层黄土覆盖；河川地区地势平坦，土壤肥沃，水源充足。该地区气候属于温带大陆性季风干旱半干旱草原气候，年平均气温8.6℃，年均降水量399 mm。横山县土壤种类丰富，形成的原因众多，在土壤类型方面具有典型的代表性。选择其为研究区，可避免单一土壤类型造成的局限性以及偶然性，使研究结果更具一般性和推广性。

1.2 土壤样品采集与制备

土壤样品为采自表层约5 cm深的土壤。在采集土壤样品时，选择地势较为平坦、土壤裸露的20个地区作为样区，如图1所示。选择样区时，考虑到各种不同的土地利用类型，每个样区内选择具有代表性的测点4或5个。每个测点采集1个样品，最终共采集84个土壤样品。采集的土壤样本需经过磨碎、风干处理，然后对磨碎的土壤样品用直径为2 mm的孔径筛进行过筛处理，最后采用重铬酸钾氧化容量法测定土壤样本中有机质含量(质量分数)[23]。

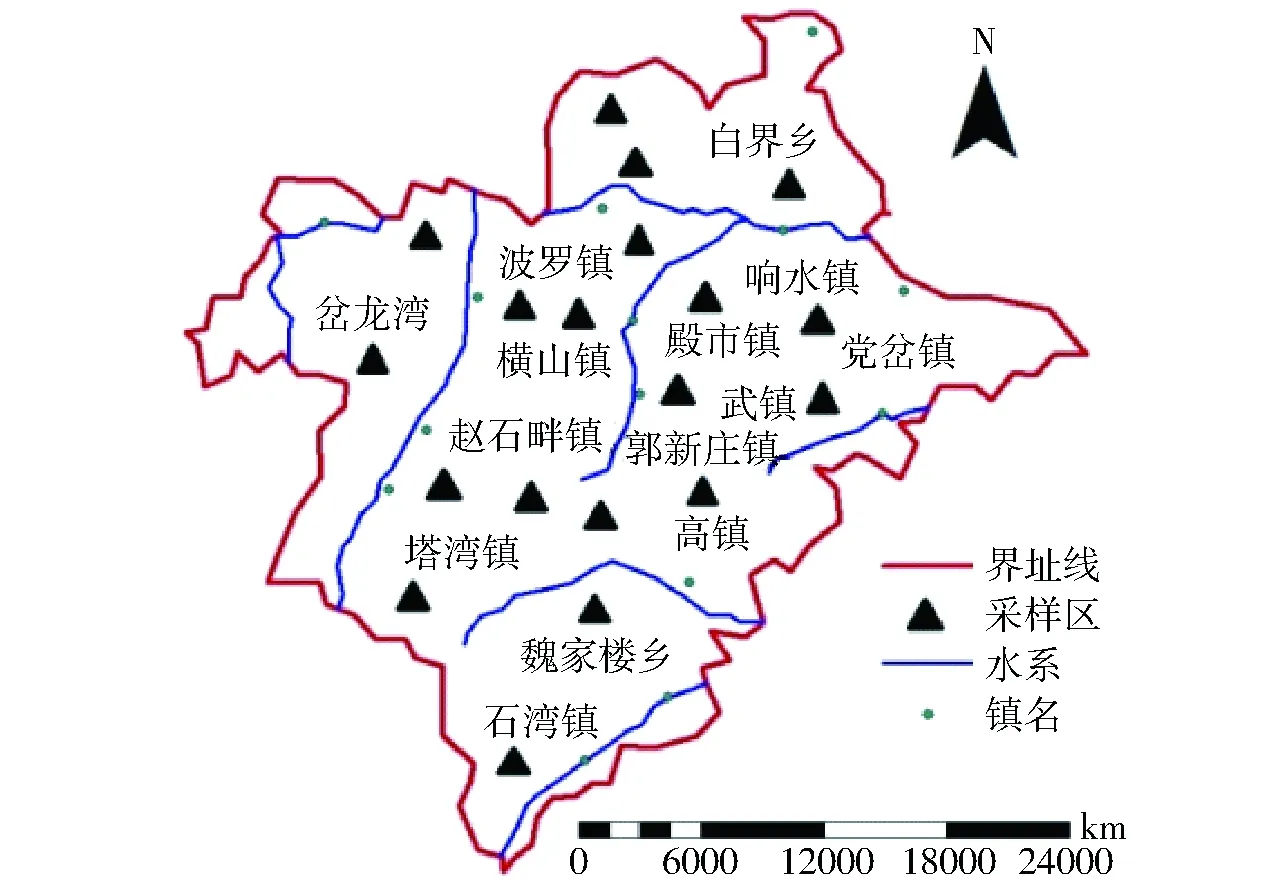
图1 土壤样本采集区域(横山县)Fig.1 Area of collecting soil samples

1.3 土壤光谱与有机质测定

采用ASD Field Spec FR地物光谱仪对土壤样品进行光谱测定(实验中统一用2 mm粒径土壤样品)，其光谱波长范围为350～2 500 nm，其中350～1 000 nm之间光谱分辨率为3 nm，1 000～2 500 nm之间光谱分辨率为10 nm。室内测定条件包括：光源为50 W的卤素灯，光源离土壤样本约50 cm。采用3°视场角的探头，探头侧面积直径约为2 cm，探测器头部垂直对准样品，距离土壤样本约20 cm。测定前先用75 cm×75 cm的白色参考板定标，为保证土壤样本充满整个视场，对一条光谱曲线的扫描时间设定为5 s，每个土壤样品的光谱重复测量4次，最后取4次反射率平均值作为土壤样品的实际光谱反射率，土壤样本原始光谱曲线如图2所示。土壤的光谱反射率和光谱特征受土壤粒径、含水率、铁、氮、钾及有机质等的共同影响，本研究在土壤样品光谱测定中，限定土壤粒径为2 mm以消除不同粒径差异对光谱反射率测定的影响，在后续具体数据反演前除去水的吸收波段影响，因此可认为反演时的光谱差异主要为土壤中有机质成分的影响。

图2为样本土壤的9条原始反射光谱曲线，可以看出，这9条光谱曲线波形基本相似，但每条光谱曲线的反射率都有所不同，随着有机质含量的增加，光谱反射率降低。

图2 不同有机质含量土壤的原始光谱反射率Fig.2 Soil original spectral reflectance with different soil organic matter contents

对上述土壤样品进行有机质含量测定。具体过程为：在加热条件下，用过量重铬酸钾-硫酸溶液对土壤中有机碳进行氧化处理，多余的重铬酸钾用硫酸亚铁氨标准溶液滴定，以样品和空白消耗重铬酸钾的差值计算有机碳含量。将测得的有机碳乘以矫正系数1.1，再乘以常数1.724即为土壤有机质含量(依据化学方法油浴加热重铬酸钾-容量法)[24]，最后共测得84组样本的有机质含量。

1.4 光谱数据变换与主成分分析

在对原始测得的数据进行光谱变换之前，首先对原始测得的光谱曲线用加权平均法进行噪声去除处理，并除去水的吸收波段，具体波段剔除范围包括1 380～1 416 nm和1 896 ～1 970 nm，得到处理后的原始光谱曲线，后文称“原始光谱”曲线、数据、反射率，都是去除了噪声及水吸收率影响后的数据。对上述处理后的光谱反射率R(λi)取倒数得到倒数光谱反射率1/R(λi)，因为光谱微分能够消除部分环境背景的影响，较好地反映土壤的本质特征，故再对倒数光谱反射率1/R(λi)求其一阶微分获得一阶导数光谱[1/R(λi)]′(简称为一阶导数光谱)[13-14]，一阶导数光谱计算式为

[1/R(λi)]′=

[1/R(λi+1)-1/R(λi-1)]/(λi+1-λi-1)

(1)

式中λi-1、λi、λi+1——相邻波长

通过上述光谱变换以及相关性分析获得相关系数较大的一阶导数光谱波段，利用这些与有机质含量相关性较大的一阶导数光谱波段参与多元线性逐步回归，有利于土壤有机质含量反演的精度与可靠性。在上述波段选择中虽然考虑了波段间的间距要求，但并未考虑这些波段数据间可能存在相关性，这种相关性对后续的定量反演不利。主成分分析可以消除这种相关性。利用PCA方法对上述提取的波段信息进行变换，在尽可能多的保留原始数据信息的前提下，可很好消除数据间的相关性。一般研究中选取采用PCA变换后的累计方差贡献率大于90%的主成分分量作为反演的参量[25]。消除了数据间的相关性，在利用神经网络进行反演时可以减少输入层神经网络个数，改善网络拓扑结构与反演效果。同时在回归分析过程中，也可以利用包含信息量更多的若干个主成分分量来代替原来波段信息特征进行回归分析，以减少信息间相关性对结果的影响。

1.5 土壤有机质含量反演模型与方法

采用基于BP神经网络和多元逐步回归分析的方法分别建立有机质含量反演模型。其中基于BP神经网络的方法，采用PCA变换后信息量占优的主成分分量作为反演变量。而在多元逐步回归方法中既采用了挑选的全部特征波段作为反演变量进行回归分析，也分别采用PCA变换后主要的主成分分量以及全部主成分分量作为反演变量进行回归分析。

1.5.1 基于BP神经网络的方法

(1)BP神经网络

在光谱分析中，BP神经网络是一种重要的模式识别方法，适合解决一些复杂的映射问题，对于复杂的非线性预测、反演具有较好的效果。本文利用该模型进行土壤有机质含量的反演，构建的BP神经网络共3层，即输入层、隐含层和输出层[26]。在利用BP神经网络反演时，减少反演变量的数量，会提高BP反演的速率，减少计算量，因此采用PCA变换后信息量占优的主成分分量作为BP神经网络的输入层来提高其反演速率。

(2)构建PCA-BP模型

构建基于PCA的土壤有机质含量BP反演模型的过程主要包括：①预处理，利用PCA技术对一阶导数光谱进行主成分分析，并提取累计方差贡献率大于90%的主成分分量作为BP神经网络的输入层因子，以相对应样本土壤有机质含量作为输出层神经元。②确定BP神经网络拓扑结构以及最佳隐含层神经元个数，本文中的隐含层神经元个数为5，并利用样本训练，得到反演神经网络模型。③利用训练获得的BP神经网络进行有机质含量反演，分析精度。对于BP神经网络反演而言，在训练过程中训练样本数量越多，得到的模型可信度越高，而用于检验模型的样本数量相对于总体样本数不能过少。

1.5.2 基于多元逐步回归分析的方法

(1)逐步回归分析原理

逐步回归分析是在考虑全部自变量中按其对因变量(y)的作用、显著程度或者贡献率，由大到小地逐个引入回归方程，而对那些对y作用不显著的变量可能不被引入回归方程，由此建立最优回归方程以便于对因变量进行预报或控制[27]。本文在建立土壤有机质含量反演的回归模型中，选用的回归参量分别为：①相关分析后挑选的全部特征波段。②通过PCA变换后得到信息量占优的主成分分量。③通过PCA变换后全部主成分分量。

(2)主成分回归分析

主成分回归(Principal component regression)是解决logistic回归分析中共线性问题的常用方法之一，它通过主成分变换，将具有相关性较高的变量的信息综合成相关性低的主成分，然后以主成分代替原变量参与回归计算，一般的主成分回归方法是取累计贡献率大于90%的主成分分量，而不是取所有主成分分量，其优点是可以减少回归参数，提高反演精度[28]。在本研究中，首先采用了一般的主成分回归方法，即PCA变换后得到信息量占优的主成分分量进行回归分析。因考虑到某些特征值低的主成分分量可能恰含有与有机质含量反演相关性较大的信息，所以也利用PCA变换后的全部主成分分量进行回归分析。

2 结果与分析

2.1 光谱变换处理结果

对原始光谱数据进行去噪处理后，通过相关性计算，发现原始光谱数据与土壤有机质含量两者呈负相关性，并且各个波段的相关性差异小、相关性系数绝对值普遍偏小(图3中原始反射光谱相关系数曲线)。而通过求倒数光谱反射率1/R(λi)与土壤有机质含量的相关性，发现其相关性比前者高，但整体还是呈负相关性。最后对变换后的一阶导数光谱数据与土壤有机质含量做相关性分析(图3中一阶导数光谱相关系数曲线)，发现该相关系数曲线在350～2 500 nm整个波长范围内相关系数正负交替，且在750～1 250 nm和1 600～1 850 nm具有较高的相关系数；由于一阶导数光谱在整个波段350～2 500 nm与土壤有机质含量的相关系数都要高于原始光谱反射率，因此认为变换后的光谱反射率比原始反射率更适合用于反演土壤有机质含量研究。根据上述的相关性分析结果提取最佳敏感波段，选取的依据：与土壤有机质含量具有较高相关性，所选择的相邻波段有一定的距离，并且不包含在噪声波段和水吸收峰波段范围内。如图3所示，由一阶导数光谱与有机质含量的相关性系数r可得：r>0.4时已属较高，因此作为筛选波段的一个原则；并且在波长间隔Δλ≈100 nm中挑选一个波段的原则进行波段选择。共选取12个相关性较高的波段，波段对应的中心波长分别为769、807、1 020、1 205、1 369、1 439、1 599、1 773、1 858、1 986、2 115、2 497 nm。

图3 原始反射光谱、一阶导数光谱与有机质含量相 关系数曲线Fig.3 Correlation coefficient curves between original spectral reflectance, reciprocal first derivative spectral reflectance and soil organic matter content

2.2 主成分PCA处理分析

利用SPSS软件对提取的12个波段一阶导数光谱进行主成分分析，获取前5个主成分的特征值及方差贡献率，结果如表1所示。

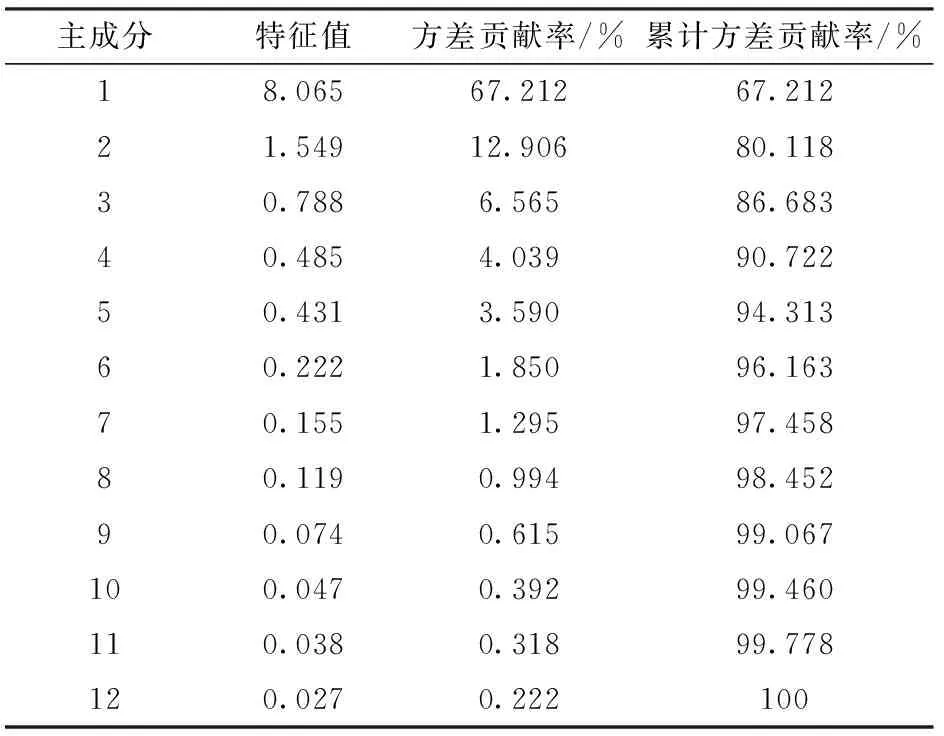
表1 PCA特征值及各自方差贡献率Tab.1 Characteristic values and respective variance contribution of PCA

表1中的方差贡献率和累计方差贡献率分别表示各个主成分所反映原始参数的信息量和这些主成分所反映原始参数数据量的总和，前5个主成分变量的累计贡献率达到94.313%，已经超过一般主成分分析要求的90%标准，因此取前5个主成分代替12个波段的一阶导数光谱信息，用于建立BP神经网络反演模型的输入，部分样本的前5个主成分分量如表2所示。

2.3 土壤有机质含量PCA-BP模型反演

从84组样本土壤有机质含量中随机抽取45组作为训练样本的学习目标，其余39组样本数据作为测试数据，构成训练集和测试集数据。然后将表2中前5个主成分得分分量作为PCA-BP反演模型输入因子，以相对应样本土壤有机质含量作为输出层神经元。神经网络训练完毕后利用所选的39组样本有机质含量作为测试数据，以检验学习获得的模型。利用39组测试数据与有机质含量实测值之间拟合得到决定系数R2以及均方根误差(Root mean square error，RMSE)。结果如图4、5所示。

表2 部分样本前5个主成分得分分量Tab.2 The first five principal component scores of partial samples

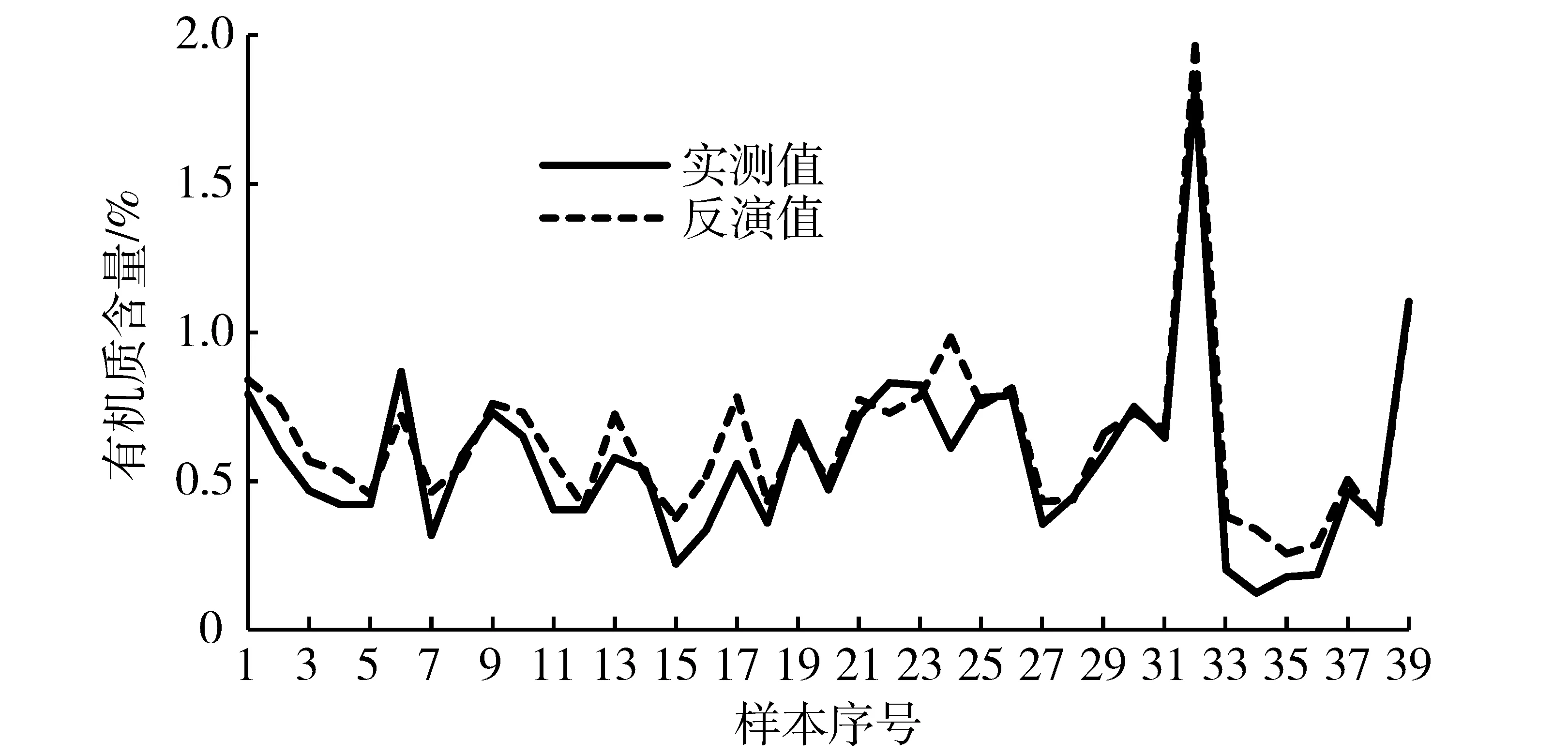
图4 土壤有机质含量实测值与反演值比较Fig.4 Comparison of measured and inversion values of soil organic matter content

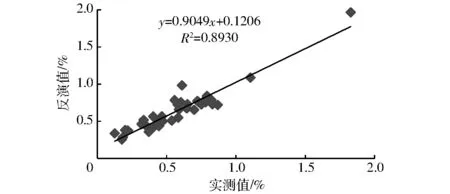
图5 土壤有机质含量实测值与反演值之间相关性Fig.5 Correlation of measured and inversion values of soil organic matter content

从图4中可以看出，BP反演模型的土壤有机质含量反演值与实测值之间的拟合效果较好，整体走向基本吻合，图5为有机质含量反演值与实测值之间的相关性分析，从图中可看出有机质含量均匀分布在直线两侧，模型决定系数R2达到0.893 0，RMSE为0.118 5%，相关性较好，与现有大量文献的R2最优值相当，说明本文建立的PCA-BP模型反演有机质含量效果较好。

2.4 土壤有机质含量多元逐步回归模型

2.4.1 基于一阶导数光谱的多元逐步回归模型

将挑选的12个特征波段对应的一阶导数光谱作为模型反演的自变量，土壤有机质含量作为因变量，依照2.3节选择45组数据作为建模数据，其余39组数据用以进行模型精度验证。进行逐步回归分析，系统通过自动剔除与组合，最终构建9个多元回归反演模型，分别对应9种波段组合方式，结果如表3所示。

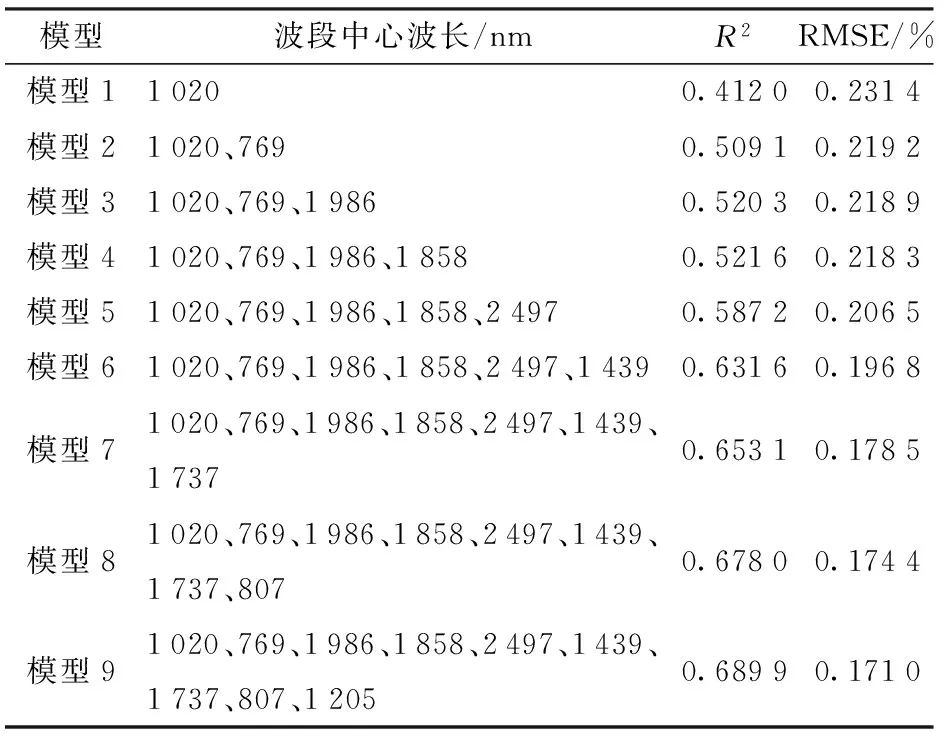
表3 9种多元回归模型及其参数Tab.3 Nine kinds of multivariate regression model and its parameters

模型1～9对应的回归方程分别为

y=0.472-124.889x1 020

(2)

y=0.376-88.825x1 020-40.63x769

(3)

y=0.370-93.026x1 020-46.234x769+1.815x1 986

(4)

y=0.387-97.398x1 020-44.63x769+8.372x1 986+

11.803x1 858

(5)

y=0.388-101.617x1 020-46.148x769+14.797x1 986+

24.645x1 858+1.339x2 497

(6)

y=0.489-116.838x1 020-37.836x769+16.308x1 986+

22.002x1 858+1.228x2 497+43.534x1439

(7)

y=0.492-144.68x1 020-36.865x769+14.892x1 986+

23.334x1 858+0.815x2 497+65.839x1 439-65.436x1 737

(8)

y=0.488-133.201x1 020-24.979x769+15.704x1 986+

23.009x1 858+1.045x2 497+73.123x1 439-

54.962x1 737-49.169x807

(9)

y=0.466-133.263x1 020-9.329x769+16.991x1 986+

21.919x1 858+1.044x2 497+87.977x1 439-60.066x1 737-

64.561x807-60.947x1 205

(10)式中y——有机质含量反演值xi——中心波长为i的波段所对应的一阶导数反射率

从表3可以看出模型1的R2最小，为0.412 0，RMSE为0.231 4%，模型9的R2达到最大，为0.689 9，RMSE为0.171 0%。从9个模型的波段组成可以看出，中心波长为1 020、769、1 986 nm的波段在建模过程中起的作用最大。9个模型反演值与实测值的比较如图6所示，最佳回归反演模型为模型9，其反演结果如图7所示。

图6 有机质含量实测值与反演值的比较Fig.6 Comparison of measured and inversion values of soil organic matter content

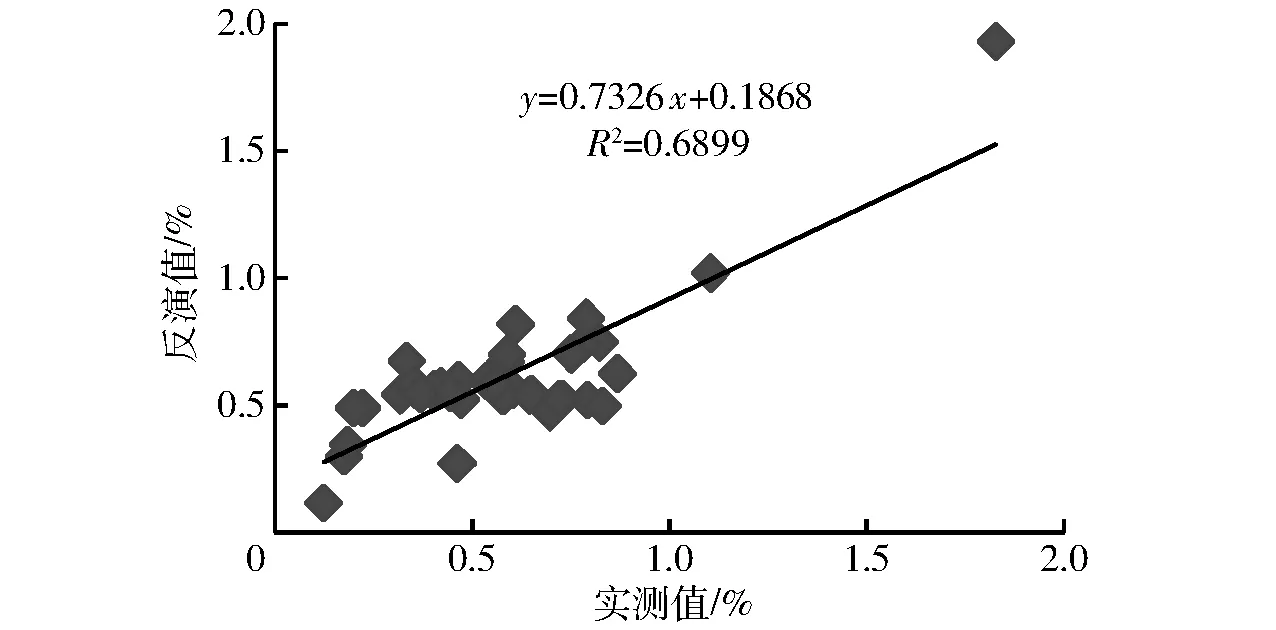
图7 模型9土壤有机质含量实测值与反演值之间相关性Fig.7 Correlation of measured and inversion values of soil organic matter content for model 9

通过对比模型1～9的反演结果可发现，模型1仅包含自变量为中心波长1 020 nm波段，其模型R2为0.412 0，RMSE为0.231 4%，而每个模型都包含此变量，说明中心波长1 020 nm波段在有机质含量反演中的作用最大。这9个模型的精度从模型1到模型9依次升高，说明随着模型中自变量个数的增加，模型的反演精度逐渐提高。

2.4.2 基于主成分分量的多元回归分析

实验数据分组情况与2.3节相同(45组样本作为建模数据，其余39组作为检验数据)。利用45组样本构建主成分回归模型。利用建立模型后得到的回归方程对其余39组有机质含量进行反演，通过反演得到的有机质含量值与实测值进行拟合分析得到回归模型的反演精度。

(1)实验1

首先采用一般的主成分回归分析[20]，用前文中12个波段一阶导数光谱经过主成分分析获得的前5个主成分分量代替原变量进行回归计算，有机质含量实测值为因变量。该实验共产生5个回归模型(模型1～5)，其对应的回归方程为

y=0.659-0.085X2

(11)

y=0.661-0.125X2-0.119X1

(12)

y=0.653-0.118X2-0.128X1-0.053X3

(13)

y=0.655-0.112X2-0.157X1-0.073X3-0.051X4

(14)

y=0.657-0.112X2-0.156X1-0.071X3-

0.052X4-0.012X5

(15)

式中X1～X5——主成分1～主成分5的主成分得分分量

模型精度结果见表4。5个模型反演值与实测值比较如图8所示，可见，其反演效果最佳，模型5的有机质含量反演值与实测值拟合见图9。

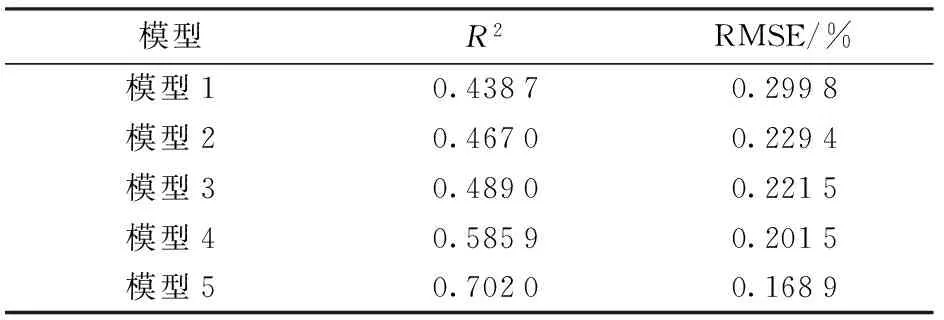
表4 5种主成分回归模型及其参数Tab.4 Five kinds of principal component regression model and its parameters

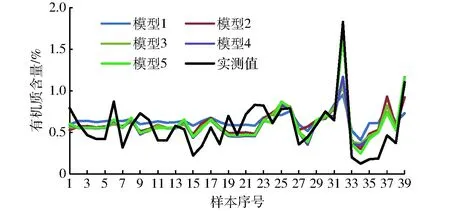
图8 有机质含量实测值与反演值的比较Fig.8 Comparison of measured and inversion values of soil organic matter content

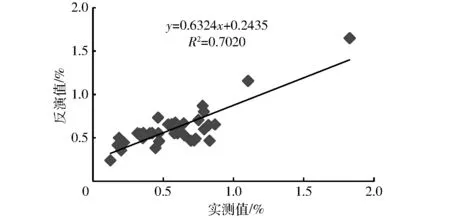
图9 土壤有机质含量实测值与反演值之间相关性Fig.9 Correlation of measured and inversion values of soil organic matter content for model 5

从表4中可以看出，模型5的反演效果最好，R2为0.702 0，RMSE为0.168 9%，其结果明显高于2.4.1 节中模型9的反演效果，说明利用PCA变换处理可以在减少多元回归参与变量个数及计算量的基础上，提高土壤有机质含量反演的精度。实验结果表明，主成分2对有机质含量反演作用最大而不是包含信息量更多的主成分1，原因在于：虽然主成分2的信息含量不如主成分1高，但其包含的信息与有机质含量的相关性更高，是反演的关键信息。这说明过去基于主成分分量的多元逐步回归中，采用仅根据特征值大小(包含信息量的多少)来作为主成分取舍的规则是有缺陷的。因此，利用全部12个主成分分量进行土壤有机质含量反演的回归分析。

(2)实验2

采用前文中12个波段一阶导数光谱经过主成分分析获得的全部12个主成分分量代替原变量进行回归计算，有机质含量实测值为因变量。该实验共产生8个回归模型(模型1～8)，其对应的回归方程为

y=0.665+0.072X12

(16)

y=0.665+0.084X12-0.102X2

(17)

y=0.666+0.078X12-0.138X2-0.109X1

(18)y=0.660+0.073X12-0.132X2-0.117X1-0.043X3

(19)

y=0.661+0.072X12-0.127X2-0.140X1-

0.060X3-0.041X4

(20)

y=0.670+0.073X12-0.144X2-0.172X1-

0.067X3-0.066X4+0.039X9

(21)

y=0.674+0.073X12-0.147X2-0.182X1-

0.062X3-0.069X4+0.042X9+0.020X8

(22)

y=0.677+0.073X12-0.147X2-0.183X1-0.061X3-

0.071X4+0.045X9+0.020X8-0.015X5

(23)

式中X8、X9、X12——主成分8、主成分9、主成分12的主成分得分分量

表5中数据为各个模型精度比较，8个模型反演值与实测值比较结果如图10所示，最佳回归反演模型为模型8，其反演结果如图11所示。

从表5可以看出，模型8的R2达到最大，为0.740 7，RMSE为0.161 3%，其反演效果明显高于实验1中最好的结果；并且仅包含主成分12的反演模型精度要高于实验1中仅包含主成分2的精度。说明虽然主成分12所含信息量在12个主成分中最少，但其所包含的信息在主成分多元回归分析中作用最大，即主成分12包含有土壤有机质含量反演的最关键信息，两者相关性最大。

综合实验1、2分析可得，一般基于主成分分量的多元回归方法虽然能够减少参与变量的个数和计算量，但是仅根据各主成分特征值大小排序来选取回归分析的变量，没有考虑各个主分量信息与反演回归的变量之间的相关性，而本研究表明，某些主成分虽含信息量少，但恰含有土壤有机质含量反演更为关键的信息。

表5 8种主成分回归模型及其参数Tab.5 Eight kinds of principal component regression model and its parameters

图10 有机质含量实测值与反演值的比较Fig.10 Comparison of measured and inversion values of soil organic matter content

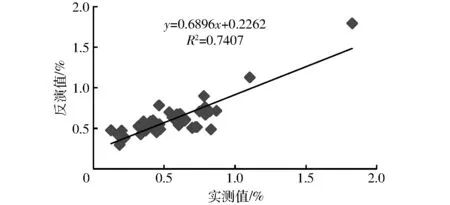
图11 土壤有机质含量实测值与反演值之间相关性Fig.11 Correlation of measured and inversion values of soil organic matter content for model 8

3 结论

(1)通过光谱变换得到的一阶导数光谱与土壤有机质含量之间的相关性明显高于原始光谱数据。其中对应中心波长分别为769、807、1 020、1 205、1 439、1 737、1 858、1 986、2 497 nm的波段与土壤有机质含量相关性较高。而在通过多元逐步回归分析建立土壤有机质含量反演模型的结果中，1 020、769、1 986 nm对反演最为重要。

(2)在利用12个特征波段的一阶导数光谱进行多元逐步回归分析与反演中，模型9的有机质含量反演效果最好。而基于PCA结果进行多元逐步回归，反演精度比基于一阶导数光谱多元逐步回归有明显的改善，所反演的有机质含量效果更佳，说明PCA可以明显提高有机质含量反演精度。此外，现有的仅依据所含信息量多少来选取主成分的方法，因未考虑各个主分量与反演回归变量之间的相关性而具有一定局限性。在本文土壤有机质含量反演中，信息量少的主成分12 与有机质含量反演具有更高的相关性，此时仅根据特征值大小而去除该主分量对反演精度会产生明显影响。在应用基于PCA的多元逐步回归方法进行反演时需要特别注意。

(3)基于PCA构建的BP神经网络模型检验结果表明，模型有机质含量反演值与实测值之间的R2达到0.893 0，RMSE为0.118 5%。与多元逐步回归分析的2种模型相比反演精度有显著提高，说明PCA-BP反演模型更适合于土壤有机质含量的反演。

1 SINGH D,HERLIN I,BERROIR J P, et al.An approach to correlate NDVI with soil color for erosion process using NOAA/AVHRR data [J].Advances in Space Research,2004,33(3):328-332.

2 CHANG C W, LAIRD D A. Near infrared reflectance spectroscopic analysis of soil C and N[J].Soil Science,2002,167(2):110-116.

3 郝国辉,邵劲松.土壤有机质含量测定方法的改进研究[J].农业资源与环境学报,2014,32(2):202-204. HAO Guohui,SHAO Jinsong. Improvement research on the measurement method for organic matter content in soil[J].Journal of Agricultural Resources and Environment,2014,32(2):202-204.(in Chinese)

4 何东健,陈煦.土壤有机质含量田间实时测定方法[J/OL]. 农业机械学报, 2015, 46(1):127-132.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150119&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.01.019. HE Dongjian, CHEN Xu. Real-time measurement of soil organic matter content in field [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(1):127-132.(in Chinese)

5 刘磊, 沈润平, 丁国香. 基于高光谱的土壤有机质含量估算研究[J]. 光谱学与光谱分析, 2011,31(3):762-766. LIU Lei, SHEN Runping, DING Guoxiang. Studies on the estimation of soil organic matter content based on hyper-spectrum [J].Spectroscopy and Spectral Analysis, 2011, 31(3):762-766.(in Chinese)

6 曾胤,陆宇振,杜昌文,等.应用红外光声光谱技术及支持向量机模型测定土壤有机质含量[J].土壤学报, 2014,51(6):1262-1269. ZENG Ying,LU Yuzhen,DU Changwen, et al. Applying infrared photoacoustic spectroscopy and support vector machine model to quantify soil organic matter content[J].Acta Pedologica Sinica,2014,51(6):1262-1269.(in Chinese)

7 郭文川, 宋克鑫, 韩文霆. 管针式土壤含水率探头设计与影响因素分析[J/OL]. 农业机械学报, 2015, 46(5):115-121.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150517&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.05.017. GUO Wenchuan, SONG Kexin, HAN Wenting. Tube-pin type soil moisture content probe and its influence factors[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2015,46(5):115-121.(in Chinese)

8 田永超,张娟娟, 姚霞,等.基于近红外光声光谱的土壤有机质含量定量建模方法[J].农业工程学报,2012,28(1):145-152. TIAN Yongchao,ZHANG Juanjuan,YAO Xia, et al.Quantitative modeling method of soil organic matter content based on near-infrared photoacoustic spectroscopy[J].Transactions of the CSAE,2012,28(1):145-152.(in Chinese)

9 ALLEN R M, LAIRD D A. Quantitative prediction of biochar soil amendments by near-infrared reflectance spectroscopy[J]. Soil Science Society of America Journal, 2013, 77(5):1784-1794.

10 FIDENCIO P H, POPPI R J, DE ANDRADE J C. Determination of organic matter in soil using near-infrared spectroscopy and partial least square regression[J]. Communication in Soil Science and Plant Analysis, 2002,33(9-10):1607-1615.

11 VISCARRAROSSEL R A, LARK R M. Improved analysis and modeling of soil diffuse reflectance spectra using wavelets [J]. European Journal of Soil Science, 2009, 60(3):453-464.

12 ABERGAZ A, WINOWIECKI L A, VAGEN T G, et al. Spatial and temporal dynamics of soil organic carbon in landscapes of the upper Blue Nile Basin of the Ethiopian Highlands[J]. Agriculture Ecosystems & Environment, 2016, 218:190-208.

13 于涛. 基于模糊识别的土壤有机质高光谱估测模型研究[D]. 泰安:山东农业大学,2013.

14 徐明星,周生路,丁卫,等.苏北沿海滩涂地区土壤有机质含量的高光谱预测[J].农业工程学报，2011,27(2):219-223. XU Mingxing,ZHOU Shenglu,DING Wei, et al.Hyperspectral reflectance models for predicting soil organic matter content in coastal tidal land area, northern Jiangsu[J].Transactions of the CSAE,2011,27(2):219-223.(in Chinese)

15 谭琨, 张倩倩, 曹茜,等. 基于粒子群优化支持向量机的矿区土壤有机质含量高光谱反演[J]. 地球科学:中国地质大学学报, 2015(8):1339-1345. TAN Kun, ZHANG Qianqian, CAO Qian, et al.Hyperspectral retrieval model of soil organic matter content based on particle swarm optimization-support vector machines[J].Earth Science-Journal of China University of Geosciences, 2015(8):1339-1345.(in Chinese)

16 侯艳军,塔西甫拉提·特依拜,买买提·沙吾提,等. 荒漠土壤有机质含量高光谱估算模型[J].农业工程学报,2014,30(16):113-120. HOU Yanjun, TASHPOLAT·Tiyip,MAMAT·Sawut, et al.Estimation model of desert soil organic matter content using hyperspectral data[J].Transactions of the CSAE,2014,30(16):113-120.(in Chinese)

17 于雷, 洪永胜,耿雷, 等. 基于偏最小二乘回归的土壤有机质含量高光谱估算[J].农业工程学报,2015,31(14):103-109. YU Lei,HONG Yongsheng,GENG Lei, et al.Hyperspectral estimation of soil organic matter content based on partial least squares regression[J].Transactions of the CSAE,2015,31(14):103-109.(in Chinese)

18 HUMMEL J W, SUDDUTH K A， HOLLIINGER S E. Soil moisture and organic matter prediction of surface and subsurface soils using an NIR soil sensor [J]. Computers and Electrics in Agriculture ,2001,32(2):149-165.

19 于士凯, 姚艳敏, 王德营,等. 基于高光谱的土壤有机质含量反演研究[J]. 中国农学通报, 2013, 29(23):146-152. YU Shikai, YAO Yanmin, WANG Deying, et al. Studies on the inversion of soil organic matter content based on hyper-spectrum[J].Chinese Agricultural Science Bulletin,2013,29(23):146-152.(in Chinese)

20 VASQUES G M, GRUNWALD S, SICKMAN J O. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra[J].Geoderma,2008,146(1-2):14-25.

21 杨扬,高小红,贾伟,等.三江源区不同土壤类型有机质含量高光谱反演[J].遥感技术与应用,2015,30(1):186-198. YANG Yang, GAO Xiaohong, JIA Wei, et al. Hyperspectral retrieval of soil organic matter for different soil types in the three-river headwaters region[J].Remote Sensing Technology and Application,2015,30(1):186-198.(in Chinese)

22 栾福明,张小雷,熊黑钢,等.基于不同模型的土壤有机质含量高光谱反演比较分析[J].光谱学与光谱分析,2013,33(1):196-200. LUAN Fuming, ZHANG Xiaolei, XIONG Heigang, et al.Comparative analysis of soil organic matter content based on different hyperspectral inversion models [J].Spectroscopy and Spectral Analysis,2013,33(1):196-200.(in Chinese)

23 韩兆迎,朱希存,刘庆,等.黄河三角洲土壤有机质含量的高光谱反演[J].植物营养与肥料学报,2014,20(6):1545-1552. HAN Zhaoying, ZHU Xicun, LIU Qing,et al. Hyperspectral inversion models for soil organic matter content in the Yellow River Delta [J].Plant Nutrition and Fertilizer Science,2014,20(6):1545-1552.(in Chinese)

24 李孝兰. 用重铬酸钾氧化容量法测定土壤有机质关键技术[J]. 现代农村科技, 2013,25(23):36.

25 于雷, 洪永胜, 周勇,等. 连续小波变换高光谱数据的土壤有机质含量反演模型构建[J]. 光谱学与光谱分析, 2016, 36(5):1428-1433. YU Lei, HONG Yongsheng, ZHOU Yong, et al. Inversion of soil organic matter content using hyperspectral data based on continuous wavelet transformation[J].Spectroscopy and Spectral Analysis,2016, 36(5):1428-1433.(in Chinese)

26 杨建锋, 马军成, 王令超,等. 基于地貌类型的土壤有机质多光谱遥感反演[J]. 农业科学与技术, 2016,17(7):48-50. YANG Jianfeng, MA Juncheng, WANG Lingchao, et al. Extraction of soil organic matter information by multi-spectral remote sensing based on diverse landforms[J]. Agricultural Science & Technology, 2016,17(7):48-50.(in Chinese)

27 王延仓, 安健, 顾晓鹤,等. 利用模拟宽波段数据定量反演关中平原土壤有机质含量研究[J]. 安徽农业科学, 2016, 44(14):240-244. WANG Yancang, AN Jian, GU Xiaohe, et al. The quantitative retrieval of soil organic matter content in Guanzhong plain by using wide band data[J].Journal of Anhui Agricultural Sciences,2016, 44(14):240-244.(in Chinese)

28 袁征, 李希灿, 于涛,等. 高光谱土壤有机质估测模型对比研究[J]. 测绘科学, 2014, 39(5):117-120. YUAN Zheng, LI Xican, YU Tao, et al.Contrast research on soil organic matter estimation model using hyper-spectral data[J].Science of Surveying and Mapping, 2014, 39(5):117-120.(in Chinese)

Comparison on Inversion Model of Soil Organic Matter Content Based on Hyperspectral Data

YE Qin1JIANG Xueqin1LI Xican2LIN Yi1

(1.CollegeofSurveyingandGeo-Informatics,TongjiUniversity,Shanghai200092,China2.CollegeofInformationScienceandEngineering,ShandongAgriculturalUniversity,Taian271018,China)

Hengshan county of Shaanxi was taken as research area, three kinds of soil organic matter content inversion model based on hyperspectral data were compared. The soil samples were collected in the field. The ASD Field Spec FR was used to measure the soil samples’ spectrum. The content of soil organic matter was measured via potassium dichromate oxidation volumetric method in laboratory. Then the first derivative of spectral data was obtained by applying the reciprocal difference to original spectral reflectance, and the multiple linear stepwise regression (MLSR) analysis model of the first derivative of spectral data was constructed. The correlations between the original spectral reflectance, the first derivative of spectrum and soil organic matter content were analyzed. The first derivative spectra of the characteristic bands which had high correlation coefficient with soil organic matter content were obtained. Based on the first derivative spectra, the MLSR model was established. Meanwhile, the principal component analysis (PCA) was performed for the first derivative spectra of the characteristic bands with high correlation coefficient. The PCA-BP model and PCA-MLSR model were established by the results of PCA. The soil organic matter content was inversed by three methods, and the inversion accuracy was validated and compared with each other. The results showed that the coefficient of determination (R2) and root mean square error (RMSE) between the measured value and inversion value were 0.893 0 and 0.118 5% with PCA-BP model, respectively, and theR2and RMSE between the measured value and inversion value were 0.740 7 and 0.161 3% with PCA-MLSR model, respectively. However, in these MLSR models which based on the first derivative spectra,R2and RMSE between the measured value and inversion value were 0.689 9 and 0.171 0% with the optimal inversion model, respectively. Based on the results, the inversion accuracy of soil organic matter content in PCA-BP model was higher than that of MLSR model. In MLSR model, the inversion accuracy of soil organic matter content by using all principal component was better than that only using the partial principal component, of which the cumulative variance contribution was greater than 90%. The content of soil organic matter can be well inversed.

soil; organic matter content; the first derivative of spectra; principal component analysis; BP neural network; multiple linear stepwise regression

10.6041/j.issn.1000-1298.2017.03.021

2016-07-29

2016-09-25

上海市科学技术委员会科研计划项目(13231203602)

叶勤(1970—)，女，副教授，博士，主要从事数字摄影测量与遥感研究，E-mail: yeqin@tongji.edu.cn

林怡(1970—)，女，副研究员，博士，主要从事遥感图像处理与分析研究，E-mail: linyi@tongji.edu.cn

S153.6+21

A

1000-1298(2017)03-0164-09