数学教学中的思维过程浅论
2017-04-17杨天府
杨天府


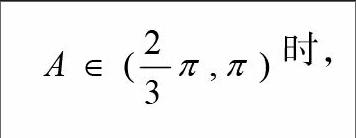
中图分类号:G632 文献标识码:B 文章编号:1002-7661(2016)19-256-02
数学教学的过程,是教师运用自己头脑中的认知结构,通过启发、诱导,促进学生头脑的同化,把教材的知识结构,认知因素转化成学生的认知结构的全过程。在数学教学中,充分暴露解题的思维过程,充分暴露解法的探索过程,通过 对思维过程的分析、探索,使思维过程进一步简捷、合理、严密,有 利于培养学生思维的严密性与创造性,有利于发展学生的思维能力,有利于进一步提高学生分析问题、解决问题的能力。
1、充分暴露解题的思维过程
数学问题的解决过程是一个思维的过程,心理学认为数学问题解决的过程是主体认识活动、思维活动同问题的客观内容相互作用的活动,在实际思维活动中,主要是对问题的分析与综合,而且这两者往往是紧密相连的,解决任何一数学问题,都要首先对问题的结构进行分析,要明确自己已知什么(条件),要求什么(目标),然后把条件和目标进行比较,找出它们内在的联系,提出解题的各种设想并选择解题的最佳方案。因此数学教学中,充分暴露解题的思维过程是非常重要的。
(1)、充分暴露解题的思维过程,可以培养学生思维的创造性。充分暴露思维过程可以从中发现一些别开生面的解题思维和解题方法,以开拓视野。
例1 如图:在多面体ABCDEF中,已知ABCD是边长为3的正方形,EF//AB,EF= ,EF国内的吗AC的距离为2,则该多面体体积为:( )
(A) (B)5
(C)6 (D)
该题中的几何是一个不规则的几何体,要计算该几何体的体积,应考虑把它转化为规则的几何体来计算。
思路1:补形法不访假设平面BCF 平面ABCD,延长FE到G,将该几何体补成一个直三棱柱,则:
思路2:分割法不妨假设平面FBC 平面ABCD,连结BE、CE,将该几何体分割成一个三棱锥和一五胡乱华棱锥,则:
思路3:作为选择还可使用排除法,为此可对几何体的体积作粗略估计,选出正确答案。
连结EB、EC,可得四棱锥E-ABCD,它的高即为EF到平面ABCD的距离,则: 原多面体的体积 ? ,从而排除A、B、C只能选D。
以上三条思路,其中(1)、(2)是正常的思维过程,也就是我们常说的通法,而(3)则是针对该题的一种特殊的解法,这种思维方式可以说是一种创造性的思维,它不因袭前人,不固步自封,思他人之未思,发现他之之未以现,这种创造性的思维不是凭空而来的,它植根于平时日积月累的不断钻研和对思维品质的良好训练。因此,在给出一道问题以后,应让学生尽可能暴露各自解题的思维过程,并及时归纳、总结,在充分肯定学生积积思维,勇于探索的前提下,总结解题思维过程的优点与不足,特别对于一些有创意的解法要给予鼓励,以激励创新意识,这对提高学生思维的灵活性、创造性大有裨益。
(2)充分暴露解题的思维过程,可以培养学生思维的严密性。对于一个命题的判断,问题的解答,不论正确也好,错误也好,只有充分暴露其思维过程,才能真正理解答案的来龙去脉以及错误原因的本质所在,从而培养学生在解题的思维过程中处处严谨,步步有据的良好的思维品质。又如有这样一道练习题:
已知A是 ABC的一个内角,
求 的辐角主值有的同学给出了如下解答:解:
=
以上的变形是完美的,正确的,解题的思路是清晰的,解的过程看起来似乎是无懈可击的,然而当把该题在课堂进行讨论的时候,有的同学指出: 究其原因,他认为 的取值与是否把 表示为三角形式密切相关,即与 是否大于零密切相关。因此需要对2cosA+1,大于、等于、小于零这三种情况分类讨论,即当 时 ,此时 ,当 时, , ,当 时, ,即 ,其辐角为任意角,其辐角主值为[0,2 ]内的任意角。
由上题我们可以进一步感觉在数学教学中充分暴露学生的思维过程对于培养学生思维的严密性,提高学生分析、解决问题的能力何等重要。
2、充分暴露解题的探索过程
美国数学家哈尔莫斯指出:数学真正的组成部分是问题和解,解题才是数学的心脏,可见解题在教学中占据相当重要的地位。德国教育学家第斯多惠曾经说过:一个好的教师应该教给学生去了现真理,也就是说,教师对于问题的讲解应始终坚持分析地讲解,要充分暴露解题思路的探索过程,即教师在讲解例题时,应该换个方位,假设我是学生,会怎么想,假设我事先并不知道这个结论,我应该怎样下手,甚至可以把自己探索失败的过程暴露给学生,说穿了,教师要讲的不是怎样做,而是为什么要这样做。如果教師忽略了这一点,解题时总演示“成功”的思路,每一个问题的解法都很正确。很巧妙,从来不展示“失败”的思路,不展示思路与方法在碰壁时怎么办。如何在有限的失败中得到正确的思路和方法,其结果只能是老师讲的精彩,学生听的轻松,但遇到题设或结论稍加改变的问题,学生往往束手无策,因此,在寻求解题思路时,要让学生逐步学会怎样分析,怎样推理,怎样选择方法,怎样解决问题。
