基于内涵亏值的概念格渐进式构建
2017-04-17吴杰,梁妍,马垣
吴 杰,梁 妍,马 垣
(1.辽宁科技大学 软件学院,辽宁 鞍山 114051; 2.辽宁科技大学 应用技术学院,辽宁 鞍山 114051)
(*通信作者电子邮箱wujieaa@163.com)
基于内涵亏值的概念格渐进式构建
吴 杰1*,梁 妍2,马 垣1
(1.辽宁科技大学 软件学院,辽宁 鞍山 114051; 2.辽宁科技大学 应用技术学院,辽宁 鞍山 114051)
(*通信作者电子邮箱wujieaa@163.com)
为了避免构建概念格时的繁琐过程,提高概念格构建的效率,提出了一种基于内涵亏值通过查找顶元素来快速渐进式生成概念格的新方法。首先,形式化地定义了顶元素、旧概念、产生概念、新概念、产生子概念、内涵亏值集合、剩留父概念、超集删除与正则队列;提出了概念格元素是否为顶元素的判定定理并给出了其证明;其次,在原概念格的正则队列中依次取概念元素,经超集删除后得到剩留父概念;最后,从剩留父概念查找其所在等价类的顶元素,逐步生成新概念格的正则队列。理论分析时间复杂度较基于属性的渐进式概念格生成(CLIF_A)算法与FastAddIntent算法有效降低,在实验例证对比中,概念数目大于150时,所用时间远少于对比算法。实验结果表明该算法方法简单,构建效率较对比算法明显提高。
概念格;内涵亏值;顶元素;超集删除;正则队列
0 引言
概念格是隶属数学概念和概念层次结构的应用数学领域[1]。理论上结构严谨,能形象地体现事物之间的泛化与特化关系,在空间聚类方法、病症智能诊断、Folksonomy、信息修复与文件浏览、软件演化分析、访问权限管理、命题集约简等诸多领域都有着成功的应用。概念格的构建是概念格应用的前提基础,但是一个背景中概念的个数是随着背景的尺寸指数级增长的(比如对于半序集中反额定标尺概念的个数是2|S|),这样背景稍大,概念的个数就多得无法计算。如何提高概念格的构建效率是当前研究的热点课题。
对于概念格构建的主要方法有两大类。一类是批处理概念格生成算法[2-4],其主要思想是先生成背景对应的全部概念,再由亚概念与超概念的连接关系,生成节点间的连线,进而完成概念格的构建;缺点是当增加对象时,需要重新构建概念格。另一类是渐进式概念格生成算法:1995年,Godin等[5]提出了概念格的渐进式生成算法,渐增式地插入新节点;2002年,谢志鹏等[6]提出了利用树状结构存储节点快速构建概念格的渐进式生成算法,有效地区别节点类型,缩小了父子节点的搜查范围;2004年,李云等[7-8]提出了基于属性的概念格渐进式生成算法及多概念格的横向合并算法,特别说明了属性拆分及策略对概念格构建效率的影响;2009年,刘群等[9]提出了基于对象和属性交叉渐进式概念格生成算法,解决了针对对象和属性交叉渐增更新需要重新构建概念格的问题;同年,刘耀华等[10]提出了新的区间数分解与定标算法,用来处理多种类型的扩展背景,给出了相应的扩展格生成算法,改进了区间值分解与模糊概念格的属性定标方法;2012年屈文建等[11]提出了一种利用最大秩的全1矩阵来生成概念格的算法,采用背景中最大秩全1子阵对应概念格的每个节点,通过横向、纵向扩充成对应的子格,再经合并构建整体概念格;2013年,姚佳岷等[12]提出了一种基于概念内涵、外延升降序的双序渐进式概念格合并算法,特点是在结构上较好地保留了原有信息;2014年,徐敏政等[13]引入元胞数据组织结构,将对象和属性分别与概念节点的外延和内涵同时求交,提出了双向渐进式概念格生成算法,解决了概念格构建带来的更新问题,避免了繁琐的合并过程;2015年,Zou等[14]通过确定概念格的顺序关系和寻找更新概念,提出了一种快速生成概念格的新算法。
以上的这些渐进式概念格生成算法可以随着增加对象(或者属性)而动态更新概念格,适用于记录渐增事务数据库类型的背景,且算法的效率都有不同程度的提高,但是,当构建概念格的概念数目巨大时,为避免构建时的复杂过程,有效地提高构建的效率,本文提出了一种基于内涵亏值,经由超集删除,通过剩留父概念查找其所在等价类的顶元素来生成概念格正则队列的全新方法,理论分析与实验对比论证均表明该渐增式构建算法是可行的,不仅方法简单有效,且在时间性能上比其他方法优越,构建效率更高。
1 概念格的定义及定理
定义1[15]若U为对象的集合,M为属性的集合,I⊆U×M为U和M之间的关系,称三元组=(U,M,I)为形式背景,简称背景。
定义2[15]若=(U,M,I)为一个背景,A⊆U,B⊆M,
f(A)={m∈M|∀u∈A,(u,m)∈I}
g(B)={u∈U|∀m∈B,(u,m)∈I}
若f(A)=B,g(B)=A,称二元组(A,B)为形式概念,简称概念。并称A为概念(A,B)的外延,B为概念(A,B)的内涵。上所有概念的集合记为B()。
性质1[15]若=(U,M,I)为一个背景,A1,A2⊆U,B1,B2⊆M,则:
1)A1⊆A2⟹f(A2)⊆f(A1);
2)A1⊆A2⟹g(A2)⊆g(A1);
3)A1⊆g(f(A1));
4)B1⊆f(g(B1));
5)f(A1)=f(g(f(A1)));
6)g(B1)=g(f(g(B1)));
7)f(A1)∩f(A2)=f(A1∪A2);
8)g(B1)∩g(B2)=g(B1∪B2)。
定义3[15]设=(U,M,I)为一个背景,(X1,Y1),(X2,Y2)∈B():
1)若X1⊆X2,称(X1,Y1)为(X2,Y2)的子概念,(X2,Y2)为(X1,Y1)的父概念,记为(X1,Y1)≤(X2,Y2)。若X1⊂X2,记为(X1,Y1)<(X2,Y2)。
2)若(X1,Y1)<(X2,Y2),且不存在(X3,Y3),有(X1,Y1)<(X3,Y3)<(X2,Y2),则称(X1,Y1)为(X2,Y2)的直接子概念,(X2,Y2)为(X1,Y1)的直接父概念,记作(X1,Y1)(X2,Y2),并称Y2-Y1为(X1,Y1)的一个内涵亏值。
定义4[15]设(M,≤)是一个半序集,若M中任何两个元素都有上确界和下确界,则称(M,≤)为一个格。
表1 在0的基础上增加对象u=6后得到的背景1
Tab.1 Formal context 1 formed by adding u=6 to original context 0
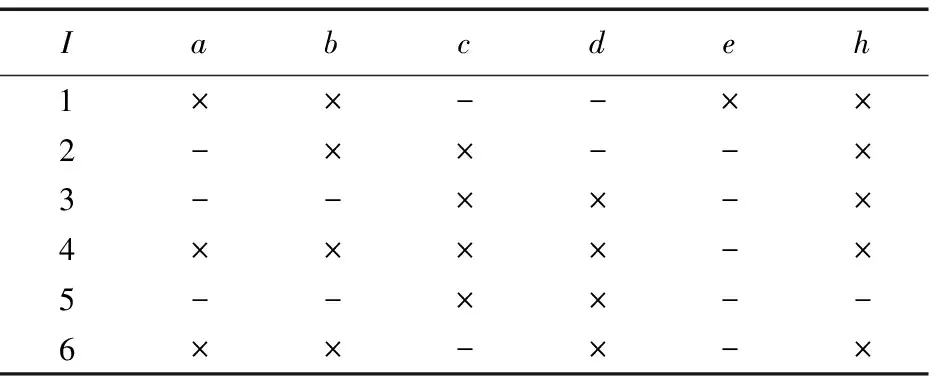
表1 在0的基础上增加对象u=6后得到的背景1
Iabcdeh1××--××2-××--×3--××-×4××××-×5--××--6××-×-×

图1 B=abdh在概念格(0)中形成的等价类

图(0)的顶元素子格

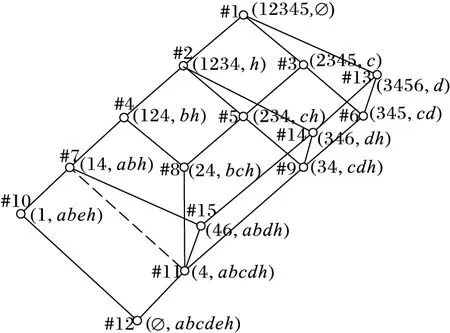
图3 背景1的概念格
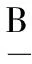
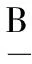
2 内涵亏值
定义6 将概念及其内涵亏值表示成(#t,X,Y,W),其中:X为外延;Y为内涵;#t中的t为自然数,是生成概念时依次赋予的概念号;W={#t1:S1,…,#tk:Sk}为(X,Y)的内涵亏值集合,其中#ti:Si表示#ti概念为(X,Y)的一个直接父概念,Si(i=1,2,…,k)表示#ti对(X,Y)的内涵亏值。
定理1 若(X,Y)的内涵亏值集合为Δ(X,Y)={S1,S2,…,Sk},且S1∩B,S2∩B,…,Sk∩B都不空,则(X,Y)是顶元素;若存在某个Si∩B=∅,则(X,Y)不是顶元素,且与Si对应的直接父概念属于同一个等价类。
证明 若(X,Y)是顶元素,则它的任意一个直接父概念(Xi,Yi),有Y∩B⊃Yi∩B,所以对于内涵亏值Si=Y-Yi,必有Si∩B=(Y-Yi)∩B=(Y∩B)-(Yi∩B)≠∅,反之若Si∩B=∅,则Si对应的直接父概念(Xi,Yi),必有(Y-Yi)∩B=∅,即Y∩B=Yi∩B,所以(X,Y)不是顶元素,且与Si对应的直接父概念属于同一个等价类。
定义7 将概念排成正则队列,所谓正则队列,即在这个队列中任何父概念都不出现在其子概念的后面。
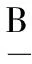
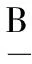
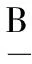
3)若其内涵亏值集合W中所有亏值与B的交都不为∅,且YB,则在(1)中有新概念(#n,X∪{u},Y∩B,W1)及产生子概念(#t,X,Y,W2)。其中:W1={#p:(Y∩B)-Y1|(#p,X1,Y1,Wp)是(X,Y)在顶元素格的直接父概念产生的概念};W2=W∪{#n:Y-B},Y-B=Y-(Y∩B)是新概念(#n,X∪{u},Y∩B,W1)对(X,Y)的内涵亏值,其中W中要删除同样是新概念(#n,X∪{u},Y∩B,W1)的直接父概念产生的内涵亏值。
为了求新概念(X∪{u},Y∩B)的内涵亏值,需求出(X,Y)在顶元素格中的各个直接父概念。为此有:
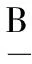
证明 因为顶元素(X,Y)与(X1,Y1)分别为等价类[(X,Y)]θ与[(X1,Y1)]θ的最大元素,所以有Y=f(g(Y∩B)),Y1=f(g(Y1∩B))。又因为在顶元素格中(X1,Y1)为(X,Y)的直接父概念,所以有Y1∩B⊂Y∩B,于是f(g(Y1∩B))⊆f(g(Y∩B)),即Y1⊆Y。然而Y1∩B⊂Y∩B,有Y1≠Y,所以Y1⊂Y,即(X1,Y1)也是(X,Y)的父概念,于是必有一个(X,Y)的直接父概念(X2,Y2)满足Y1⊆Y2⊂Y,有Y1∩B⊆Y2∩B⊆Y∩B,但因为(X1,Y1)在顶元素子格中是(X,Y)的直接父概念,所以有Y2∩B=Y1∩B或者Y2∩B=Y∩B。由于(X,Y)也是顶元素,有Y2∩B≠Y∩B,所以Y2∩B=Y1∩B。
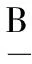
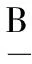
为了方便地鉴别(X,Y)的哪些直接父概念所在等价类的顶元素为(X,Y)在顶元素格中的直接父概念,给出如下形式化的定义。
定义8 若概念(X,Y)的亏值集合为W,B⊆M:
1)若W=∅(最大概念的情况),则W相对于B的超集删除为∅。
2)若W={S1,S2,…,SK},在集合{Si∩B,Si+1∩B,…,SK∩B}中将是其他元素的超集删除,相同的值只留一个。
称其结果为W相对于B的超集删除,简称为超集删除。称这些未被删除的内涵亏值对应的直接父概念为(X,Y)的剩留父概念。
显然剩留父概念所在等价类的顶元素为(X,Y)在顶元素格中的直接父概念。
例3 如图1所示,#11概念的内涵亏值集合为Δ(4,abcdh)={cd,ad,ab},这些内涵亏值与B=abdh的交分别为cd∩abdh=d,ad∩abdh=ad,ab∩abdh=ab,将是其他元素超集的删除,剩下d及ab。d及ab所对应的内涵亏值为cd及ab,cd及ab所对应的直接父概念#7及#9为剩留父概念,它们所在等价类的顶元素为#11概念在顶元素格中的直接父概念。又如图1所示,#9概念的内涵亏值集合为Δ(34,cdh)={#5:d,#6:h},这些内涵亏值与B=abdh的交分别为d∩abdh=d,h∩abdh=h,超集删除后还为d及h,d及h所对应的直接父概念是#5概念及#6概念,它们为剩留父概念。#6概念所在等价类的顶元素就是本身,#5概念所在等价类的顶元素为#2概念,由此#2概念及#6概念为#9概念在顶元素格中的直接父概念。
利用剩留父概念查找其所在等价类的顶元素方法如下。
由定理1,检查它的各个内涵亏值Si与B的交是否为∅,都不为∅,则为顶元素。若存在某个Si∩B=∅,则Si对应的直接父概念(Xi,Yi)与(X,Y)在同一个等价类中。于是对(Xi,Yi)做如上的检查,直到存在某一个概念,其内涵亏值与B的交都不为空为止,此时这个概念就是(X,Y)直接父概念所在等价类的顶元素。若某个内涵亏值Si,有Si∩B=∅,则任何一个内涵亏值Sj∩B都为它的超集,于是超集删除的结果一定是{#i:∅}。所以是否存在某个Si∩B=∅,可用超集删除的结果是否为{#i:∅}来判定。
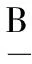
#9概念内涵亏值集合中的d对应的直接父概念是#5概念,由于是正则队列,所以#5概念已出现在L1中,又由于#5概念的内涵亏值集合为Δ(234,ch)={#2:c,#3:h},超集删除得{#2:∅},所以在L1中继续向上找#2概念,#2概念的内涵亏值集合为Δ(1234,h)={#1:h},超集删除得{#1:h},不是{#i:∅},所以#2概念为#14概念(346,dh)的一个直接父概念,且内涵亏值为:Si∩B=d∩abdh=d。
#9概念内涵亏值集合中的h对应的直接父概念是#6概念,由于是正则队列,所以#6概念已出现在L1中,又由于#6概念的内涵亏值集合为Δ(345,cd)={#3:d,#13:c},超集删除得{#13:∅},所以在L1中继续向上找#13概念,#13概念的内涵亏值集合为Δ(3456,d)={#1:d},超集删除得{#1:d},不是{#i:∅},所以#13概念为#14概念的一个直接父概念,且内涵亏值为:Si∩B=h∩abdh=h。
即#14概念在L1中的直接父概念有两个,#2概念及#13概念,且内涵亏值分别为:d及h。
3 概念格构建算法
1)内涵亏值集合的超集删除子程序CO(W)。
输入:W={#t1:S1,…,#tk:Sk}(允许W=∅)。其中,#ti:Si表示Si为相对于概念#ti的内涵亏值。 输出:{#tp:Sp∩B,…,#tq:Sq∩B}(允许是∅)。
方法:
IfW= ∅ Then 输出∅,结束 ElseFori= 1 tokForj= 1 tokIfi≠j,Si∩B⊇Sj∩B且#ti:Si未作删除标记 Then #ti:Si作删除标记 //因为是⊇,不是⊃,所以最终相同值只留一个 Exit(j)
//退出j循环 EndIf
Next(j)
Next(i)
输出{#t:S∩B|#t:S未作删除标记},结束
EndIf
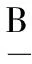
2)查找#t概念所在等价类顶元素的子程序Top(#t,V)。
输入:#t,V。其中,#t为概念的概念号,#V为概念的内涵亏值集合。 输出:#i,为#t所在等价类顶元素的概念号。
方法:
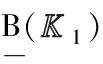
//再向上查找Else输出#t,结束 //#t为顶元素,输出#tEndIf
EndIf
3)添加新对象后的概念格及内涵亏值的计算ADD(L,u,B,n)。
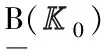
L1:=∅
Foreach(#t,X,Y,W) inLby order doWB:=CO(W)
//WB中存放W超集删除的结果IfWB仅有一个元素 #i:∅Then(#t,X,Y,W)送入L1队尾
//#t不为顶元素,直接送入L1ElseIfY⊆BThen(#t,X∪{u},Y,W)送入L1队尾 //#t为顶元素,且Y⊆B,则外延加u后送L1ElseW1:=∅IfBW≠∅ThenForeach(#i:Si∩B)inWB 在L1中取概念号为#i的概念(#i,C,D,V) 令W1:=W1∪{Top(#i,V):Si∩B}Next
EndIf
n:=n+1
(#n,X∪{u},Y∩B,W1)送入L1队尾
W2:={#i:Si|(#i:Si)∈W且#i未出现在W1中}
W2:=W2∪{#n:(Y-B)}
(#t,X,Y,W2)送L1队尾
EndIf
EndIf
Next
输出L1结束。
L:=(#1,∅,M,∅)
//L为只有一个元素(#1,∅,M,∅)的队列n:=1For each (u,B) inADD(L,u,B,n)L:=L1Next
输出L,结束。
在硬件配置为CPUInteli3 2.40GHz,内存为8GB,在VisualStudio2010的环境下,用VB.Net语言实现本文提出的概念格构建算法,与文献[14]和文献[7]算法进行了比较,随机生成20个形式背景,概念个数从50开始递增到500,变化基数为50,实验结果如图4所示,当概念的数目小于100时,三种算法的区别并不明显,当概念的数目逐渐变大(大于150)时,本文提出的概念格构建算法的运行时间更快,效果更优越,证明了其算法的有效性。
4 结语
本文提出了一种基于内涵亏值快速构建概念格的新方法:
1)将原概念格排成正则队列后依次取概念元素。
2)所取概念的内涵亏值集合作超集删除。
3)由定理1判定,若为顶元素且元素内涵不是B的子集,则得到产生子概念与新概念;若为顶元素且元素内涵是B的子集,则得到产生概念。
4)由定理1判定,若不为顶元素,经由剩留父概念继续向上查找,查找其所在等价类的顶元素,逐步生成新概念格的正则队列。
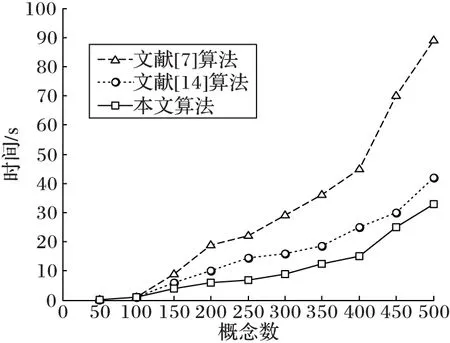
图4 三种算法运行时间对比
同时给出了概念格构建的算法。三种算法实验结果的对比,表明本文提出的方法显著提高了构建概念格的效率,为数据挖掘进一步的应用研究创造了良好的条件。
对于文章提出的方法,可以给出一些技巧使步骤简化,是进一步研究的方向。
)
[1]WILLER.Restructuringlatticetheory:anapproachbasedonhierarchiesofconcepts[C]//ICFCA’ 09:Proceedingsofthe7thInternationalConferenceonFormalConceptAnalysis.Berlin:Springer, 2009: 445-470.
[2]LINDIGC.Fastconceptanalysis[M]//WorkingwithConceptualStructuresContributionstoICCS2000.Aachen,Germany:ShakerVerlag, 2000: 152-161.
[3]STUMMEG,TAOUILR,BASTIDEY,etal.Fastcomputationofconceptlatticesusingdataminingtechniques[C]//Proceedingsofthe7thInternationalWorkshoponKnowledgeRepresentationMeetsDatabases.[S.l.]:VLDBEndowment, 2010: 129-139.
[4] 陈震,张娜,王甦菁.一种基于概念矩阵的概念格生成算法[J].计算机科学,2010,37(9):180-183.(CHENZ,ZHANGN,WANGSJ.Newalgorithmofgeneratingconceptlatticebasedonconcept-matrix[J].ComputerScience, 2010, 37(9): 180-183.)
[5]GODINR,MISSAOUI,R,ALAOUIH.IncrementalconceptformationalgorithmbasedonGalois(concept)lattices[J].ComputationalIntelligence, 1995, 11(2):246-267.
[6] 谢志鹏,刘宗田.概念格的快速渐进式构造算法[J].计算机学报,2002,25(5):490-496.(XIEZP,LIUZT.Afastincrementalalgorithmforbuildingconceptlattice[J].ChineseJournalofComputers, 2002, 25(5): 490-496.)
[7] 李云,刘宗田,沈夏炯,等.基于属性的概念格渐进式生成算法[J].小型微型计算机系统,2004,25(10):1768-1771.(LIY,LIUZT,SHENXJ,etal.Attribute-basedincrementalformationalgorithmofconceptlattice[J].JournalofChineseComputerSystems, 2004, 25(10): 1768-1771.)
[8] 李云,刘宗田,徐晓华,等.多概念格的横向合并算法[J].电子学报,2004,32(11):1849-1854.(LIY,LIUZT,XUXH,etal.Horizontalunionalgorithmofmultipleconceptlattices[J].ActaElectronicaSinica, 2004, 32(11): 1849-1854.)
[9] 刘群,冷平,孙凌宇.基于对象和属性交叉的渐进式概念格生成算法[J].计算机工程,2009,35(7):59-60.(LIUQ,LENGP,SUNLY.Incrementalconceptlatticeformationalgorithmbasedonalternateobjectandattribute[J].ComputerEngineering, 2009, 35(7): 59-60.)
[10] 刘耀华,周文,刘宗田.一种区间数分解与定标算法及其扩展形式背景的概念格生成方法[J].计算机科学,2009,36(10):213-216.(LIUYH,ZHOUW,LIUZT.Intervalscalingalgorithmanditsconceptlatticeconstructionfromextendedformalcontext[J].ComputerScience, 2010, 37(9): 180-183.)
[11] 屈文建,谭光兴,邱桃荣.运用全1矩阵的概念格生成算法[J].小型微型计算机系统,2012,33(3):558-564.(QUWJ,TANGX,QIUTR.Newalgorithmofgeneratingconceptlatticeusinguniversalmatrix[J].JournalofChineseComputerSystems, 2012, 33(3): 558-564.)
[12] 姚佳岷,杨思春,李心磊,等.双序渐进式概念格合并算法[J].计算机应用研究,2013,30(4):1038-1040.(YAOJM,YANGSC,LIXL,etal.Incrementaldoublesequencealgorithmofconceptlatticeunion[J].ApplicationResearchofComputers, 2013, 30(4): 1038-1040.)
[13] 徐敏政,何宗宜,刘亚虹,等.双向渐进式概念格生成算法[J].小型微型计算机系统,2014,35(1):172-176.(XUMZ,HEZY,LIUYH,etal.Bidirectionalincrementalformationalgorithmofconceptlattice[J].JournalofChineseComputerSystems, 2014, 35(1): 172-176.)
[14]ZOULG,ZHANGZP,LONGJ,etal.Afastincrementalalgorithmforconstructingconceptlattices[J].ExpertSystemswithApplications, 2015,42(9): 4474-4481.
[15] 马垣,曾子维,迟呈英,等.形式概念分析及其新进展[M].北京:科学出版社,2011:11-31.(MAY,ZENGZW,CHICY,etal.FormalConceptandit’sNewProgress[M].Beijing:SciencePress, 2011: 11-31.)
[16] 梁妍,吴杰,马垣,等.基于概念格亏值的共轭对方法研究[J].计算机工程与设计,2014,35(1):171-176.(LIANGY,WUJ,MAY,etal.Researchonmethodofconjugatepairsbasedonwanedvaluesfromconceptlattice[J].ComputerEngineeringandDesign, 2014, 35(1): 171-176.)
ThisworkispartiallysupportedbytheNationalNaturalScienceFoundationofChina(61273019),theYouthFundofUniversityofScienceandTechnologyLiaoning(2014QN21).
WU Jie, born in 1981, Ph.D.candidate, lecturer.His research interests include database and data mining, formal concept analysis.
LIANG Yan, born in 1982, M.S., lecturer.Her research interests include database and data mining, formal concept analysis.
MA Yuan, born in 1941, Ph.D., professor.His research interests include database and data mining, formal concept analysis.
Incremental formation of concept lattice based on intent waned value
WU Jie1*, LIANG Yan2, MA Yuan1
(1.SchoolofSoftware,UniversityofScienceandTechnologyLiaoning,AnshanLiaoning114051,China;2.SchoolofAppliedTechnology,UniversityofScienceandTechnologyLiaoning,AnshanLiaoning114051,China)
Concerning the tedious process during the construction of concept lattice, to improve the efficiency of building concept lattices, a new incremental method of constructing concept lattice based on intent waned value by seeking top elements was proposed.Firstly, top element, original concept, produced concept, new concept, producer concept, the set of intent waned values, reminded parent concept, superset delete and regular queue were formally defined; the judging theorem and proof whether the concept elements were top elements were given.Secondly, the elements were extracted from the regular queue of the original lattice in due order and the reminded parent concepts were got after superset delete.Finally, the top elements were found from the equivalent classes of the reminded parent concepts and the regular queue of the new lattice was gradually generated.Time complexity was effectively reduced compared with the Attribute-based Concept Lattice Incremental Formation (CLIF-A) algorithm and the FastAddIntent algorithm by theory analysis.In comparison with simulated experiments, the time consumption of the proposed algorithm was far less than the comparative approaches in large size of population.The simulation results show that the proposed algorithm is simple, and can effectively improve the time performance, meanwhile provides better performance in construction efficiency.
concept lattice; intent waned value; top element; superset delete; regular queue
2016-06-14;
2016-08-22。
国家自然科学基金资助项目(61273019);辽宁科技大学青年基金资助项目(2014QN21)。
吴杰(1981—),男,山东蓬莱人,讲师,博士研究生,主要研究方向:数据库与数据挖掘、形式概念分析; 梁妍(1982—),女,辽宁鞍山人,讲师,硕士,主要研究方向:数据库与数据挖掘、形式概念分析; 马垣(1941—),男,北京人,教授,博士,主要研究方向:数据库与数据挖掘、形式概念分析。
1001-9081(2017)01-0222-06
10.11772/j.issn.1001-9081.2017.01.0222
TP18
A
