M-TAEDA：多变量水质参数时序数据异常事件检测算法

毛莺池，齐 海，接 青，王龙宝

(河海大学 计算机与信息学院，南京 211100)

(*通信作者电子邮箱maoyingchi@gmail.com)

M-TAEDA：多变量水质参数时序数据异常事件检测算法

毛莺池*，齐 海，接 青，王龙宝

(河海大学 计算机与信息学院，南京 211100)

(*通信作者电子邮箱maoyingchi@gmail.com)

在供水管网中部署传感器网络实时获取多个水质参数时间序列数据，当供水管网发生污染时，高效准确地检测水质异常是一个重要问题。提出多变量水质参数时间异常事件检测算法(M-TAEDA)，利用BP模型分析多变量水质参数的时序数据，确定可能离群点；结合贝叶斯序贯分析独立更新每个参数的事件概率，预测单个传感器节点检测的异常概率；将单变量的事件概率融合为统一多变量事件概率，融合判断异常事件。实验结果表明：BP模型模拟多变量水质参数进行预测可以达到90%精确度；与单变量参数时间异常事件检测算法(S-TAEDA)相比，M-TAEDA可以提高异常检出率约40%，降低误报率约45%。

无线传感器网络；异常事件检测；BP模型；多变量水质参数；时间序列数据

0 引言

在供水管网中部署传感器网络实时获取水质指标数据，当供水管网发生污染时，传感器感知的水质参数数据也有异常变化，实时预警污染事件。研究[1]表明，能够明显反映水质的参数主要有游离氯、总有机碳(Total Organic Carbon, TOC)、电导率(Electrical Conductivity, EC)、pH值、温度、浊度。面对网络中多个水质参数时间序列数据，高效准确地检测水质异常是一个重要问题。然而，现有的水质异常检测算法大都基于单个检测指标是否超标来判断供水管网水质污染异常事件[2-3]。由于单个参数考虑的因素单一，易造成漏报误报。本文提出多变量水质参数时间异常事件检测算法(Temporal Abnormal Event Detection Algorithm of Multivariate time-series, M-TAEDA)，基于多个水质参数作出融合决策，判断供水管网污染异常事件。M-TAEDA采用人工神经网络进行水质模拟，通过BP(Back Propagation)模型分析多变量水质参数的时序数据，确定可能的离群点；结合贝叶斯序贯分析独立更新每个参数的事件概率，预测单个传感器节点在一段时间内是否有异常事件发生；最后对单变量的事件概率融合为一个统一的多变量事件概率作出融合判断，检测供水管网的异常事件发生。实验结果表明：BP模型模拟多变量水质参数进行预测可以达到90%精确性；与单变量参数时间异常事件检测算法(Temporal Abnormal Event Detection Algorithm of Single-variate time-series, S-TAEDA)相比，M-TAEDA方法可以提高异常检出率40%，降低误报率45%。

1 相关工作

基于水质参数的异常事件检测方法通常包含两个阶段：一是建模阶段，以历史监测数据作为训练数据，建立水质预测模型；二是测试阶段，将新观测数据与预测数据比较，判定水质是否正常。文献[4]采用基于双阈值的异常事件检测方法，通过设置两个阈值，提高算法的检测精度。但是，仅仅根据阈值判定异常事件，精确度不高，无法捕捉监测数据的时空特征，导致较高误报率。文献[5]采用基于模式的异常事件检测方法，根据用户历史行为模式建模，推测当前行为中有无异常，当模式匹配时，则认为当前模式有异常事件发生。Byrt等[6]提出基于统计模型的检测方法，假设水质参数服从高斯分布，计算测试样本数据的均值和方差，通过较比测量值与计算值的差值，判断水质异常。基于统计的异常检测方法的缺点是要求假设水质数据集必须符合特定分布，无法满足实际场景应用需求。基于机器学习的异常检测常用BP神经网络、支持向量机、动态贝叶斯网络和马尔可夫随机场等方法检测异常[7-9]。文献[10]以在线监测氨氮值为对象，利用RBF(Radial Basis Function)神经网络和小波分析的判别在线水质数据是否异常。Perelman等[11]提出了一种基于贝叶斯网络(Bayesian Network, BN)的异常检测算法，基于BN的统计数据估算供水网中污染物的可能位置及其传播路径，检测污染事件。上述方法都单独局限于基于单个水质指标是否超标，判断供水网中水质污染事件。但是，单个检测指标不符合真实的供水管网环境，当污染事件发生时，多个水质参数都明显异常。单个参数考虑的因素单一，易造成漏报和误报，导致精度不高。因此，本文根据多个水质参数数据变化，基于多个水质参数作出融合决策，判断供水管网污染事件。

2 问题陈述

传感器部署在供水管网中实时监测水质参数数值变化，判断水质污染情况。供水管网拓扑结构如图1所示，水质传感器部署在管道连接处检测水质参数，用连通图G=〈V,E〉表示，V表示水质传感器节点集合，E表示边集合。每个节点有一个唯一的编号，从1到n。供水管网中每个节点处部署了多个传感器节点检测多种水质参数，如游离氯、电导率(Electrical Conductivity, EC)、pH值、温度、总有机碳(Total Organic Carbon, TOC)和浊度[1]。仅仅检测一个水质参数判定污染异常可能造成较大检测偏差，需要综合考虑6个监测分量为多变量水质监测因子，观测6个监测分量在一段时间的序列数据，经过融合判断，确定该节点处是否有水质异常事件发生。如图1所示，节点1处部署传感器监测6个水质参数数据，结合6个水质因子的监测数据综合判断水质。

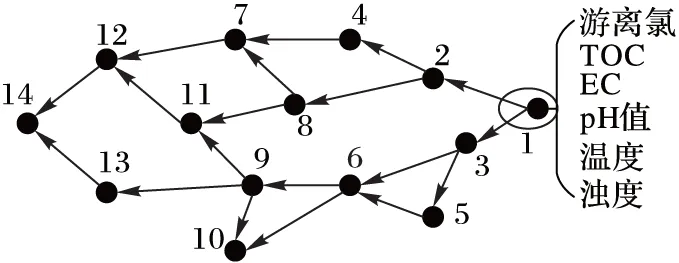
图1 供水管网拓扑结构实例

水质异常指水质数据偏离正常，水质异常可分为离群点和异常事件两类。离群点是指某一时刻，水质数据的预测值与其实际测量值的残差超过了误差可以接受的范围。异常事件是指监测点的水质参数在一段时间内监测数据持续偏离正常模式，认为该水质参数有异常。通常，离群点较常见，可能是噪声数据，不应将其作为水质预警指标。异常事件是离群点在一段连续时间内，数据持续偏离正常预期值，则可能是污染所导致，这是本文所关注的异常事件。

3 M-TAEDA主要思想

多变量水质参数时序数据异常事件检测方法分为两个阶段：1)离线阶段——训练和构造数据驱动的预测模型(BP模型)，分析多变量水质时序数据，进行模型评估；2)在线阶段——即M-TAEDA的执行步骤，首先利用训练得到的BP模型计算预测值，比较实测值与预测值，进行误差估计和分类，结合序贯贝叶斯分析确定水质异常事件概率。两个阶段的工作流程如图2～3所示。

图2 离线阶段流程

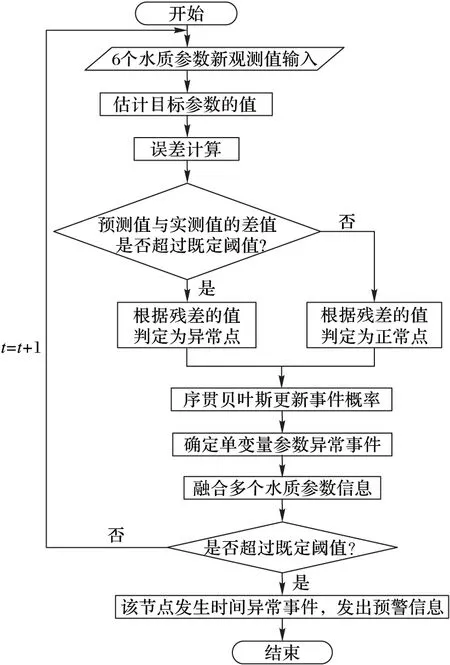
图3 M-TAEDA(在线阶段)流程

离线阶段 选择BP网络模拟6个水质参数，根据残差确定可能的离群点。BP网络不需要理解输入端与输出端之间的相互关系，适合非线性、复杂多变的水质系统，比较符合多变量水质参数处理应用场景。BP模型前向计算及其误差反向传播的特性，通过多次训练可以得到比较理想的预测模型，提高水质参数的预测精度。

在线阶段 多变量水质数据异常事件检测包括4个步骤。

1)数据分析。通过BP模型模拟水质参数之间的相互作用。

2)识别异常值。计算残差，每个水质参数在训练阶段得到固定的阈值，将观察值归类为正常或异常值。

3)确定单变量参数异常事件。基于误差结果的分类，通过序贯更新贝叶斯更新确定单变量水质参数的事件概率。

4)融合决策。来自多个水质监测指标的信息融合，提供统一的决策结果，确定供水管网在具体节点处是否有异常事件发生。

其中，本文在步骤1)和2)中采用真实的供水管网数据集训练模型。在每个时刻，当得到新的实测值后，重复执行步骤1)～4)。

应用BP神经网络分析多个水质参数间的相互作用，并根据残差确定可能的离群点；通过递归应用贝叶斯规则更新事件的概率，将监测异常点转换为单变量的异常事件概率；通过相关系数(R2)，均方误差(Mean Square Error, MSE)，融合矩阵，ROC(Receiver Operating Characteristic)曲线，检出率(Rate of Detection, RD)和误报率(False Alarm Rate, FAR)来评估算法性能；最后，综合考虑6个水质参数事件概率，确定阈值，对污染异常事件作出预警。

4 M-TAEDA方法

4.1 BP模型模拟水质参数

在供水管网中，各个传感器节点监测的实测值不仅由该水质参数决定，而且与其他参数的实测值密切相关。以游离氯为例，若仅根据游离氯单一水质参数的历史数据进行建模，得到预测模型并计算预测值，预测值与实测值并未有很大偏离，但是，此时其他水质参数的实测值与正常状态有明显偏离。其原因是水质参数间相互作用，游离氯的实测值也产生了较大偏差，仅根据单一水质参数变量建立预测模型，准确性较低。本文采用BP模型，通过输入多个水质参数，训练BP模型能够较真实地反映水质变量间的相互关系，提高预测模型的预测精确度。本文构建的BP网络如式(1)所示：

(1)

其中：wjk、wij表示权重，w0、w0j表示偏差，φ和φ0分别为激活函数与输出函数，xi表示水质参数，fk(x,w)表示估计的目标值。

供水管网中的各个监测指标相互影响，针对多变量水质参数异常事件检测，需要为每个目标水质参数，构造与训练相应的BP模型，估计目标水质参数及其相互关系。每个BP模型对应模拟每个水质参数xi(t)(i=1,2,…,6)，分别为游离氯、TOC、EC、pH、温度和浊度。每个BP模型的输入参数包括某一时刻其他几个水质参数数据和目标水质参数前一时刻的数据。在每一时刻，共有6个输入，如式(2)所示：

(2)

例如，以游离氯为目标水质参数，构建相应的BP模型结构，如图4和式(3)所示：

(3)

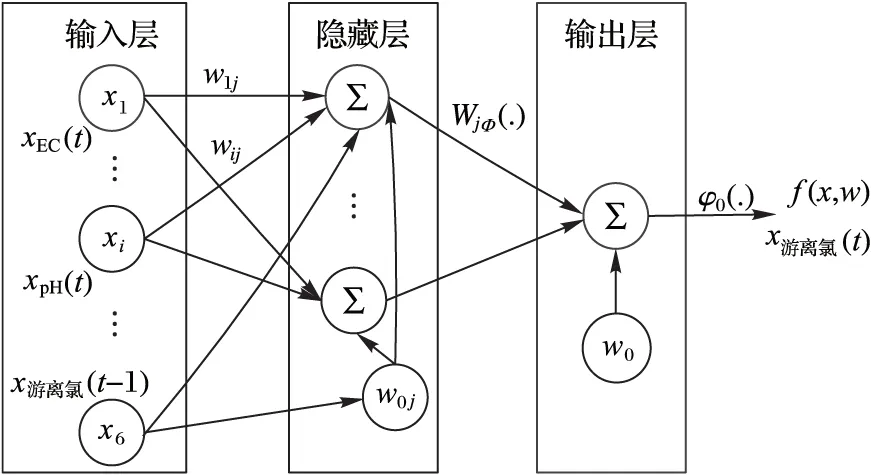
图4 游离氯参数的BP网络结构

4.2 误差评估与分类

利用历史数据对模型不断训练，构建数据驱动的BP模型。训练得到的BP模型预测供水管网中的水质参数数据，将预测值与实测值进行比较，确定预测误差，进行误差评估和分类分析。计算测量值和预测的水质参数值之间的差异可以得到估计误差，如式(4)所示：

(4)

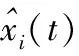
对于每个BP模型而言，估计的残差都是有界的，通过模型训练得到最优阈值。当某一时刻某水质参数的估计残差超过阈值，则被认为是离群值。为了将水质参数的正常状况与发生污染异常相区分，计算的残差ERi(t)作为“正常”“异常”的分类标准。利用训练得到的阈值进行误差分类，如果测量值在阈值范围内，表明没有异常事件发生，属于正常状况。在训练阶段，通过查看多次实验后的每个水质参数残差值，可以发现落在[96%,99%]这个上限和下限范围内的残差是可以接受的残差；若残差超过此范围，判定为异常值。

4.3 序贯贝叶斯更新

在不断训练BP模型的过程中，算法性能可以用混淆矩阵[12]来衡量。利用混淆矩阵进行模型分类，将所有观察值分为4类。真正类(TruePositive,TP)：真实的异常事件发生时，残差归类为一个离群点。假正类(FalsePositive,FP)：在正常情况下，残差归类为一个离群点。真负类(TrueNegative,TN)：在正常情况下，残差归类为合理的模型错误。假负类(FalseNegative,FN)：真实的异常事件发生时，残差归类为合理的模型错误。如表1所示。

表1 4种情况记号定义

RD和FAR是异常事件检测性能评价常用标准。RD表示检测出异常的数目占实际发生异常总次数的比值。FAR表示检测出的虚假异常占所有决策次数的比值，如式(5)所示：

(5)

在序贯贝叶斯概率更新阶段，对每个新观察值而言，事件的概率通过序贯贝叶斯分析[11]来更新。通过序贯贝叶斯分析，将检测到的异常点转换为污染异常事件的概率。在序贯分析中，观察值的数量事先不知；相反，观察值顺序读取，需要对当前的状态作出决策。每次经过序贯更新后，进行三种判断：有事件、无事件、额外观察。本文序贯更新后有两种状态：离群点和正常值，如式(6)所示。初始情况下，事件的概率很低，对于每次新到的观测值，事件的后验概率通过贝叶斯规则序贯更新，用式(7)可以计算得到：

(6)

(7)

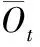
在本文应用中，污染事件的初始概率设为10-5，污染事件发生的阈值概率设为PThreshold=0.7。在这个阶段，每个参数的概率各自更新。如果某个参数事件更新的概率超过该参数设定的阈值，表明该参数发生异常事件。仿真实验模拟污染异常事件下，每个水质参数的更新概率，结果如表2。从表2中看出在08:20，6个参数中有一个参数确定有异常事件发生；在09:00，有3个参数确定了异常事件，发出预警。另外，从08:20到17:00时间段，随着污染事件发生，概率逐渐增加；当污染事件结束时，概率逐渐减少，当概率超过阈值时，发出相应报警。

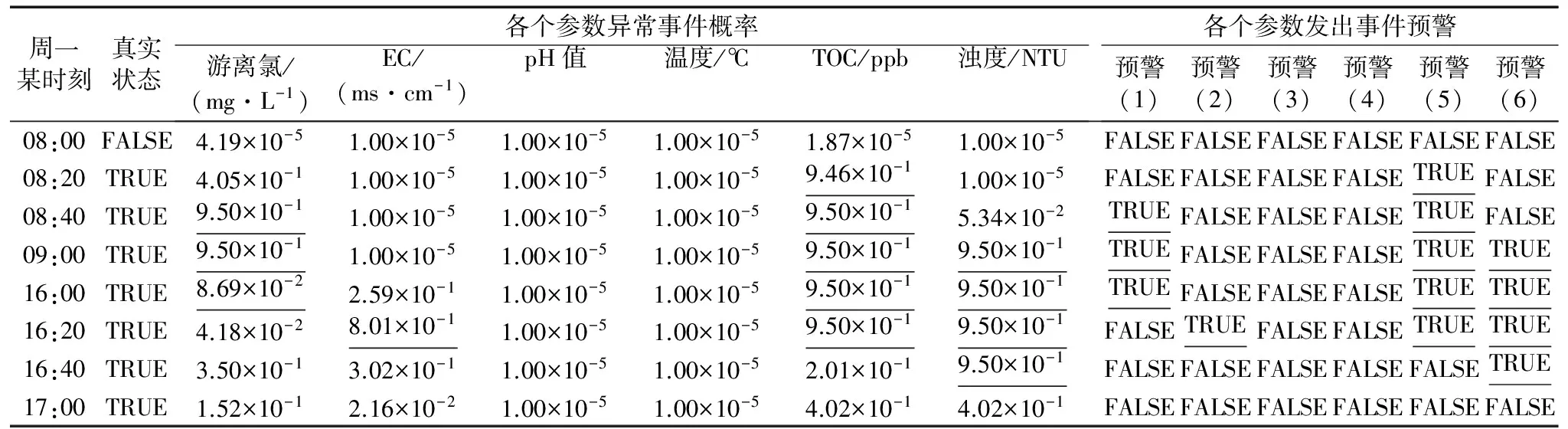
表2 污染事件概率更新

4.4 多变量融合决策

在每个时间段，通过单变量的事件概率融合为一个统一的多变量事件概率，可以反映一个事件基于所有参数的概率。此外，水质参数的权重也反映其对融合决策的影响。水质污染异常事件发生时，不同的水质参数对污染的预测能力不同。本文采用文献[1]中的方法为6个水质参数指标分配不同权重，在每个时间段，通过融合单变量的事件概率计算多参数变量的事件概率。

在模拟污染异常事件的情况下，在Matlab上完成仿真实验，模拟10个污染事件，单变量的水质参数概率更新的结果，表示在模拟污染异常事件的情况下，经过序贯贝叶斯更新后6个单变量水质参数的异常事件概率，如图5所示。以游离氯的单变量水质参数概率为例，黑线表示模拟的10次污染事件，点线表示在一定时间间隔，游离氯水质参数预测污染异常事件的概率。本文将污染异常事件发生的阈值概率设为PThreshold=0.7。每个水质参数事件更新的概率超过阈值0.7，表示在这一段时间间隔，该单变量参数有异常事件发生。从图5可以看出，模拟10个污染事件多次运行平均结果显示，游离氯指标检测出了7个异常事件，存在3次错误预警。其他5个水质参数的检测结果从图5中可以看出：EC指标检测出6个异常事件中，有1次错误预警；pH值指标检测出了5个异常事件，有1次错误预警；温度指标检测出了5个异常事件，没有错误预警；TOC指标检测出了9个异常事件，有3次错误预警；浊度指标检测出了8次异常事件，有2次错误预警。

将6个水质参数分配对应权重后，单变量的事件概率融合为一个统一的多变量事件概率。图6显示了6个事件概率图，其中：事件被预测出的概率为1，未被预测出的概率为0。每个子图表示了考虑一个或多个不同权重的水质参数得到的概率。例如，图6预警(1)表示有一个水质参数超过设定阈值，声明发生污染事件。在这种情况下，大多数事件能够被检测到。从图6预警(1)中可以看出检测出了10个异常事件中的9个，检出率很高，但是误报率也比较高，有4次错误预警。预警(2)表示至少两个或者更多个参数发出预警，表明发生了污染异常事件。在这种情况下，只有一个事件未被检测，有2次错误预警。从图6中可以看出，对于多变量参数指标而言，当3个参数融合发生预警时，检测精确度和误检率之间能达到比较好的权衡，误报率降到了0次。当4个或4个以上参数融合预警时，没有发生误报，但是检出率也降低了。从图6中可以看出，需要根据检出率和误报率做一个权衡，达到最佳检测效果。根据图6可以看出，本文确定当在一段时间内，供水管网中某个节点有3个或以上的水质参数经过序贯贝叶斯更新，概率超过给定的阈值PThreshold=0.7时，经过融合决定，认为在该节点发生了水质污染异常事件。

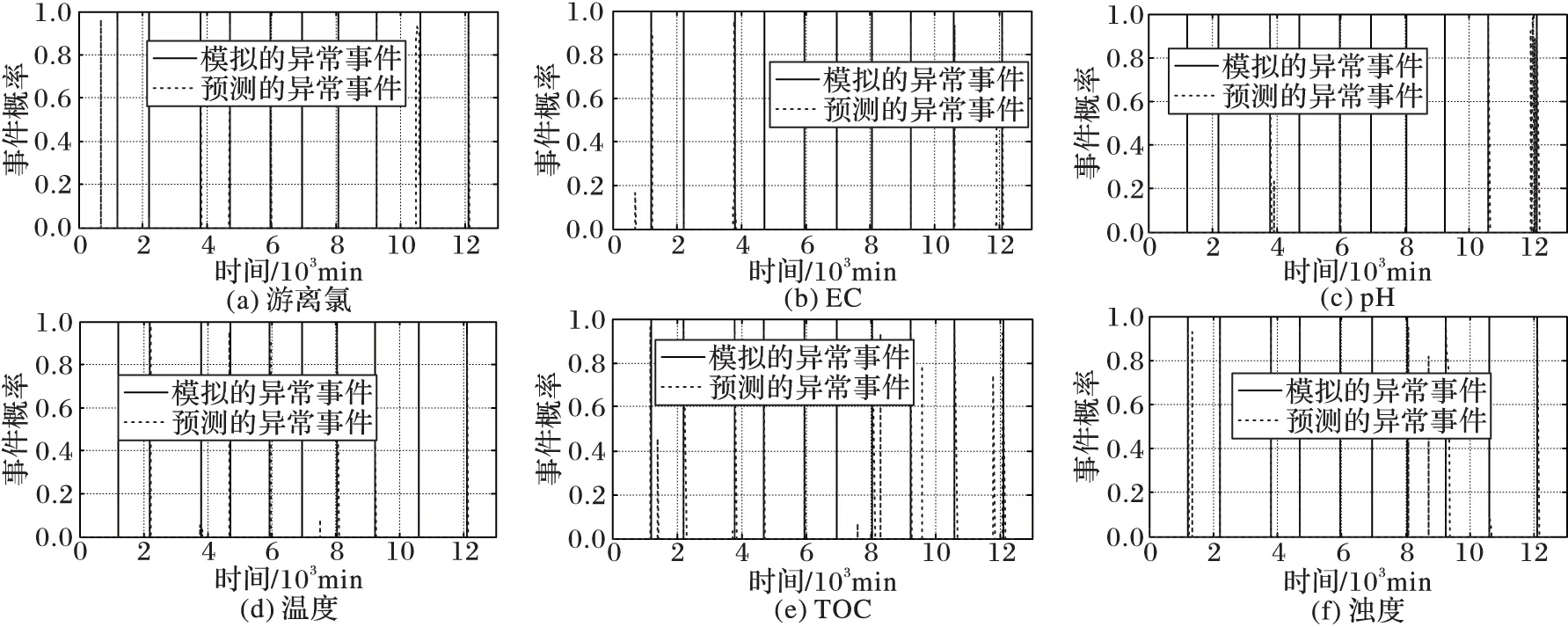
图5 单变量参数的事件概率

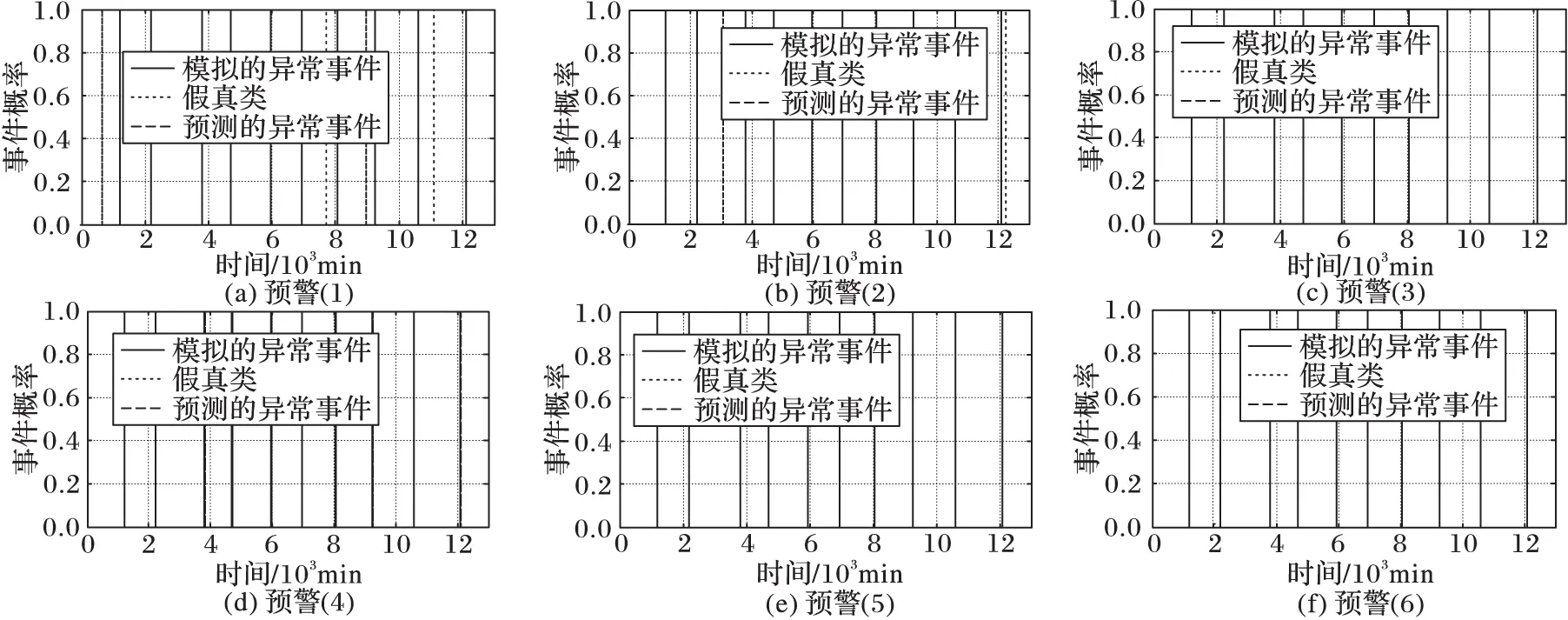
图6 多变量参数的事件概率

5 实验验证

5.1 实验环境设置

实验数据来自于从CANARY[13]获得的供水管网的真实水质数据集，在供水管网正常水质状况下每5 min采集一次(大约35 000个时间段)。检测下列水质参数：游离氯、电导率(EC)、pH值、温度、总有机碳(TOC)和浊度。通过在正常水质数据上引入泛型干扰来叠加污染异常事件[14]。将数据集分2个子集：67%数据用于训练，33%数据用于测试。

实验准备：由于污染物的异常行为对水质参数的影响在真实的供水管网系统不能实际地测试，对测量的时间序列数据通过引入泛型干扰来模拟污染异常事件。在常规数据上叠加模拟的异常事件，反映由污染异常事件引起水质参数的数据变化。事件模拟的方案是根据文献[15]提出方法，假定污染事件的分布形态是高斯分布，如图7显示本实验的6个水质参数在正常情况和叠加的污染异常事件情况下的部分时间序列。

实验分为两个部分：1)BP模型预测效果验证。BP模型模拟多变量水质参数时序数据，结合贝叶斯序贯分析独立更新每个参数的事件概率，BP模型的预测精度关系到M-TAEDA检测精确度，所以验证BP模型的预测精度。2)与S-TAEDA对比分析。控制变量，仅仅考虑一个水质参数，即将M-TAEDA与单变量参数时间异常事件检测算法S-TAEDA在相同的实验条件下进行对比分析，通过多项评价指标的对比分析来验证算法的优势。实验结果将从ROC曲线下面积、检出率RD、误报率FAR指标来验证模型的预测精确度。

5.2 实验结果分析

5.2.1 BP模型预测效果验证

本文选择前67%的数据作为训练数据，后33%作为测试数据。根据训练数据建模得到数据驱动的BP预测模型，用测试子集来评估该BP预测模型。对每个水质参数的新观测值，计算其残差作为总误差。考虑均值(Mean)、标准差(Standard Deviation, STD)、MSE(均方误差)和相关系数(R2)估计参数，表3列出了6个水质参数在BP模型训练阶段和测试阶段的结果。从表3中可以看出，在训练阶段6个水质参数数据的均值、标准差的预测值与实测值相差很小，均小于0.035。这表明该数据集没有过多的噪声数据，数据能够反映水质实际状况。另一方面，在测试阶段，6个水质参数的预测值与实测值相差不大，标准差、均方误差可接受，各个参数的相关系统差异也不大。从表3可以看到，BP模型的预测精度达约90%，效果理想，表明BP模型能够正确地分辨出水质正常与异常。

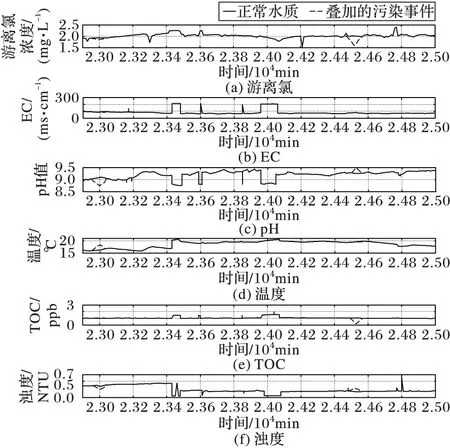
图7 多变量参数时间序列

表3 BP模型训练和测试阶段的结果

Tab.3 Training results and test results with BP model

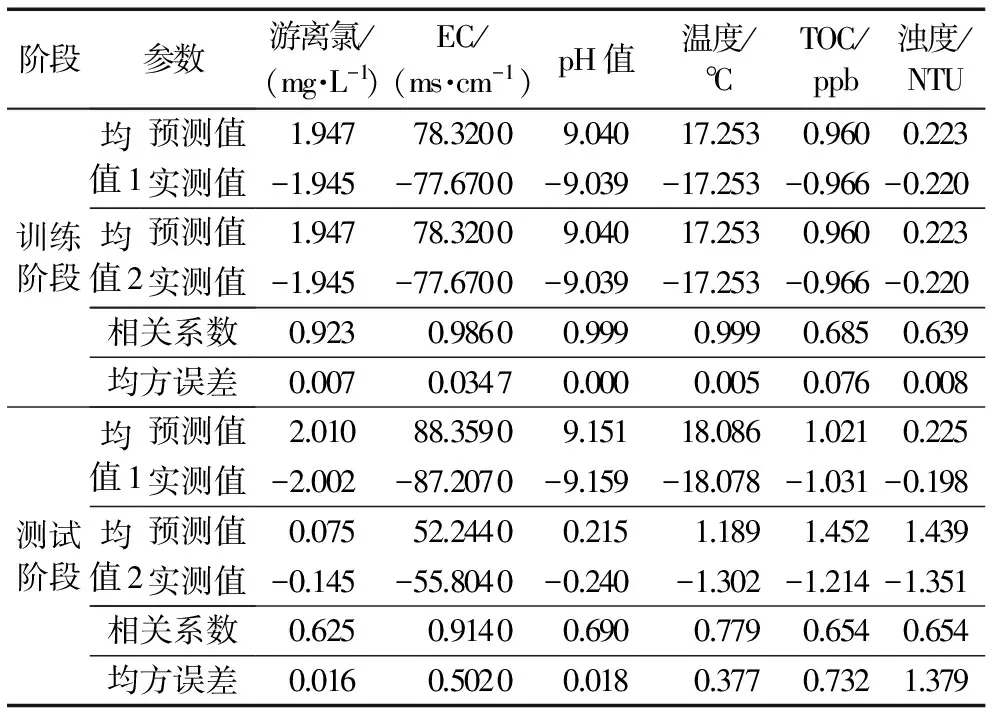
阶段参数游离氯/(mg·L-1)EC/(ms·cm-1)pH值温度/℃TOC/ppb浊度/NTU训练阶段测试阶段均值1均值2预测值实测值预测值实测值相关系数均方误差均值1均值2预测值实测值预测值实测值相关系数均方误差1．94778．32009．04017．2530．9600．223-1．945-77．6700-9．039-17．253-0．966-0．2201．94778．32009．04017．2530．9600．223-1．945-77．6700-9．039-17．253-0．966-0．2200．9230．98600．9990．9990．6850．6390．0070．03470．0000．0050．0760．0082．01088．35909．15118．0861．0210．225-2．002-87．2070-9．159-18．078-1．031-0．1980．07552．24400．2151．1891．4521．439-0．145-55．8040-0．240-1．302-1．214-1．3510．6250．91400．6900．7790．6540．6540．0160．50200．0180．3770．7321．379

5.2.2 与S-TAEDA对比分析

本文提出M-TAEDA用BP模拟各个水质参数，根据不同的水质参数对污染的预测能力不同，为多个水质参数分配对应的权重，可以大幅度降低单个参数检测算法的误报率对整个检测结果影响。从图8～9可以看出，模拟多次异常事件，M-TAEDA的检出率基本在75%以上，S-TAEDA的检出率基本在50%～60%，平均比S-TAEDA高约40%。同时，M-TAEDA的误报率都小于10%，相对于S-TAEDA约15%以上的误报率，误报率下降了45%。实验结果表明了本文提出的多变量参数的时间异常事件检测算法在检出率与误报率方面都较优。

ROC曲线是检出率和误报率一种更直观的表现，以可视化的方式表示RD和FAR之间的权衡关系。本实验通过设定出多个不同的临界值，计算出S-TAEDA和M-TAEDA的多个检出率和误报率的值。图10显示了S-TAEDA与M-TAEDA的ROC曲线。从图10中可以看出，M-TAEDA的ROC曲线下面积明显大于比S-TAEDA，表明M-TAEDA比S-TAEDA的检测精确度高，误报率低，检测效果理想。

图8 两种算法检出率的对比

图9 两种算法误报率的对比

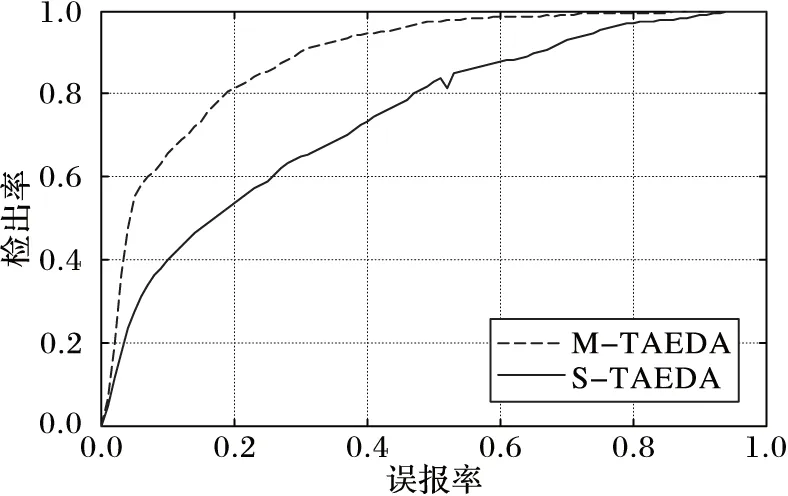
图10 两种算法对应的ROC曲线

从上述两个指标比较分析看出，本文提出的多变量参数水质异常事件检测算法M-TAEDA比单变量参数水质异常事件检测算法S-TAEDA具有很明显优势。这是因为M-TAEDA用BP模拟各个水质参数，预测目标参数下一个时刻的监测值，较符合真实应用场景中多个水质参数之间相互影响的实际情况；另外，由于不同水质参数对污染的预测能力不同，为多个水质参数分配相应权重，综合考虑多个参数的事件概率作出融合决策并预警。而S-TAEDA仅仅通过模拟一个水质参数，容易造成比较高的误报率。

6 结语

本文提出多变量水质参数时序数据异常事件检测的方法(M-TAEDA)，引入BP模型模拟供水管网中的水质参数，结合序贯贝叶斯更新确定单个水质参数的异常事件概率，最终将单变量事件概率融合为统一的多变量事件概率，最终作出融合判断，预测供水管网单个节点的异常事件。实验结果表明BP模型模拟多变量水质参数进行预测可以达到90%精确性；与S-TAEDA方法相比，M-TAEDA方法可以提高异常检出率约40%，降低误报率约45%。

References)

[1] HALL J, HERRMANN J G.On-line water quality parameters as indicators of distribution system contamination [J].Journal American Water Works Association, 2007, 99(1): 66-77.

[2] HUANG T, MA X, JI X, et al.Online detecting spreading events with the spatio-temporal relationship in water distribution networks [M]// Advanced Data Mining and Applications.Berlin: Springer, 2013: 145-156.

[3] STOTEY M V, GAAG B V D, BURNS B P.Advances in on-line drinking water quality monitoring and early warning systems [J].Water Research, 2011, 45(2): 741-747.

[4] YIM S J, CHOI Y H.Fault-tolerant event detection using two thresholds in wireless sensor networks [C]// Proceedings of the 15th IEEE Pacific Rim International Symposium on Dependable Computing.Piscataway, NJ: IEEE, 2009: 331-335.

[5] XUE W, LUO Q, WU H.Pattern-based event detection in sensor networks [J].Distributed & Parallel Databases, 2012, 30(1): 27-62.

[6] BYRT D, CARLSON K H.Expanded summary: real-time detection of intentional chemical contamination in the distribution system [J].Journal American Water Works Association, 2005, 97(7): 130-133.

[7] WANG X R, LIZIER J T, OBST O, et al.Spatiotemporal anomaly detection in gas monitoring sensor networks [C]// EWSN 2008: Proceedings of the 5th European Conference on Wireless Sensor Networks.Berlin: Springer, 2008: 90-105.

[8] UUSITAL L.Advantages and challenges of Bayesian networks in environmental modelling [J].Ecological Modelling, 2014, 203(3/4): 312-318.

[9] ELIADED G, LAMBROU T P, PANAYIOTOU C G, et al.Contamination event detection in water distribution systems using a model-based approach [J].Procedia Engineering, 2014, 89: 1089-1096.

[10] 侯迪波,陈玥,赵海峰,等.基于RBF神经网络和小波分析的水质异常检测方法[J].传感器与微系统,2013,32(2):138-141.(HOU D B, CHEN Y, ZHAO H F, et al.Based on the RBF neural network and wavelet analysis the water quality of anomaly detection method [J].Transducer and Microsystem Technologies, 2013, 32(2): 138-141.)

[11] PERELMAN L, OSTFELD A.Bayesian networks for source intrusion detection [J].Journal of Water Resources Planning and Management, 2012, 139(4): 426-432.

[12] 孔英会,景美丽.基于混淆矩阵和集成学习的分类方法研究[J].计算机工程与科学,2012,34(6):111-117.(KONG Y H, JING M L.Classification method based on confusion matrix and the integrated learning research [J].Computer Engineering and Science, 2012, 34(6): 111-117.)

[13] MURRAY R, HAXTON T, et al Water quality event detection systems for drinking water contamination warning systems: Development testing and application of CANARY [EB/OL].[2016-06-20].https://cfpub.epa.gov/si/si_public_file_download.cfm?p_download_id=496189.

[14] KLISE K A, MCKENNA S A.Multivariate applications for detecting anomalous water quality [C]// Proceedings of the 2006 Symposium on Water Distribution Systems Analysis.Cincinnati, OH: American Society of Civil Engineers, 2011: 1-11.

[15] MCKENNA S A, WILSON M, KLISE K A.Detecting changes in water quality data [J].Journal American Water Works Association, 2008, 77(1): 74-85.

This work is partially supported by the National Natural Science Foundation of China (U1301252), the National Science and Technology Support Program (2013BAB06B04), the National Key R&D Program (2016YFC0400910), the Technology Project of China Huaneng Group Company Headquarters (HNKJ13-H17-04), the Science and Technology Project of Yunnan Province (2014GA007), the Special Fund for Basic Scientific Research of Central Universities (2015B22214).

MAO Yingchi, born in 1976, Ph.D., associate professor.Her research interests include distributed computing and parallel processing, distributed data management.

QI Hai, born in 1994, M.S.candidate.His research interests include distributed computing, parallel processing.

JIE Qing, born in 1989, M.S.candidate.Her research interests include distributed computing, parallel processing, data management.

WANG Longbao, born in 1977, lecturer.His research interests include intelligent data processing.

M-TAEDA: temporal abnormal event detection algorithm for multivariate time-series data of water quality

MAO Yingchi*, QI Hai, JIE Qing, WANG Longbao

(CollegeofComputerandInformation,HohaiUniversity,NanjingJiangsu211100,China)

The real-time time-series data of multiple water parameters are acquired via the water sensor networks deployed in the water supply network.The accurate and efficient detection and warning of pollution events to prevent pollution from spreading is one of the most important issues when the pollution occurs.In order to comprehensively evaluate the abnormal event detection to reduce the detection deviation, a Temproal Abnormal Event Detection Algorithm for Multivariate time series data (M-TAEDA) was proposed.In M-TAEDA, it could analyze the time-series data of multiple parameters with BP (Back Propagation) model to determine the possible outliers, respectively.M-TAEDA algorithm could detect the potential pollution events through Bayesian sequential analysis to estimate the probability of an abnormal event.Finally, it can make decision through the multiple event probability fusion in the water supply systems.The experimental results indicate that the proposed M-TAEDA algorithm can get the 90% accuracy with BP model and improve the rate of detection about 40% and reduce the false alarm rate about 45% compared with the temporal abnormal event detection of Single-Variate Temproal Abnormal Event Detection Algorithm (S-TAEDA).

Wireless Sensor Network (WSN); abnormal event detection; Back Propagation (BP) model; multivariate water quality parameter; time-series data

2016-08-05;

2016-08-24。 基金项目:国家自然科学基金资助项目(U1301252)；国家科技支撑计划项目(2013BAB06B04)；国家重点研发计划项目(2016YFC0400910)；中国华能集团公司总部科技项目(HNKJ13-H17-04)；云南省科技计划项目(2014GA007)；中央高校基本科研业务费专项资金资助项目(2015B22214)。

毛莺池(1976—)，女，上海人，副教授，博士，CCF会员，主要研究方向：分布式计算与并行处理、分布式数据管理； 齐海(1994—)，男，安徽安庆人，硕士研究生，主要研究方向：分布式计算、并行处理； 接青(1989—)，女，山东烟台人，硕士研究生，主要研究方向：分布式计算、并行处理、数据管理； 王龙宝(1977—)，男，江苏盐城人，讲师，主要研究方向：智能数据处理。

1001-9081(2017)01-0138-07DOI:10.11772/j.issn.1001-9081.2017.01.0138

TP393;TP

A