基于三维模型的螺杆钻具传动轴螺纹强度评价研究*
2017-04-16练章华林铁军罗泽利
练章华, 刘 洋, 林铁军, 于 浩, 罗泽利 , 郝 军
(1.西南石油大学 油气藏地质及开发工程国家重点实验室,四川 成都 610500;2.中国石油集团钻井工程技术研究院 江汉机械研究所,湖北 荆州 434000)
0 引言
近年来油气开采工程中螺杆钻具已经获得了广泛应用,但是国产螺杆钻具总体上寿命短且不够稳定,螺杆钻具的失效严重影响生产,造成重大的经济损失,传动轴又是螺杆钻具中最薄弱的环节之一。目前,现场存在传动轴结构存在多种螺纹型号,但用的较多的为直扣型连接螺纹,国内外许多学者针对管柱连接螺纹的做过相关的研究,如白鹤、袁光杰等[1-3]利用有限单元法对拉伸条件下,当螺纹承载面角度越大时,接头滑脱趋势越明显,当螺纹承载面角度越小时,则接头断裂趋势越明显,为确定影响油套管螺纹粘扣失效的主要因素提供了理论依据;陈祖志,吕拴录等[4-6]对钻杆接头螺纹宏观形貌、化学成分、接头材料的力学性能、金相组织进行全面的分析,结果表明螺纹接头材质、材料的力学性能均符合标准要求,在螺纹旋合过程中发生错扣是导致接头螺纹粘扣的主要原因;张攀等[7]计算分析钻杆接头螺纹在受钻压、扭矩及钻井液压力时,钻杆发生弯曲变形前、后各螺纹牙受力和应力分布规律;韩传军等[8-9]应用故障树分析法建立了以传动轴总成失效为顶事件的故障树模型,对提高螺杆钻具的可靠性与安全性有一定的参考价值;练章华等[10-12]用弹塑性有限元法对套管偏梯形螺纹和圆形螺纹滑脱过程的对比分析表明在深井、超深井和复杂井套管柱设计中, 为套管接头螺纹的选择提供了理论数据。上述这些研究没有针对传动轴连接螺纹的力学强度做过分析,有关螺纹分析仅仅局限在二维模型分析,没有做过相关三维分析,因此不能分析螺纹在扭矩和弯矩下的应力变化。本文主要借鉴上述研究成果,分析现场传动轴粘扣及断裂事件的原因,提出一种带螺旋升角直扣螺纹连接的力学模型,对其进行有限元计算,得到与前述不同的结论,为进一步研究传动轴连接螺纹的受力提供一种新的认识,对完善螺纹设计和现场使用提供参考。
1 螺杆钻具结构及工作原理
单弯壳体+PDC钻头的螺杆钻具(简称PDM)主要由以下5部分组成:旁通阀总成、马达总成、防掉总成、万向轴总成和传动轴总成,其结构示意见图1。螺杆钻具在工作过程中[13-14],定子固定,转子在高压钻井液驱动下绕定子的轴线作行星运动。万向轴总成则把转子行星运动中的自转部分传递给传动轴,使传动轴作定轴转动,以驱动装在它下端的钻头,螺杆钻具把钻井液的水力能转化为钻头的机械能,从而破岩钻进。

图1 螺杆钻具结构示意Fig.1 Structural illustration of PDM
因为井眼轨迹是1条空间曲线,针对注采管柱运动特点,管柱在井底必然会发生疲劳,井下管柱会发生整体弯屈疲劳[15],常用空间直角坐标系Oxyz和自然坐标系OsTNB两种坐标系描述井眼轨迹,如图2所示。
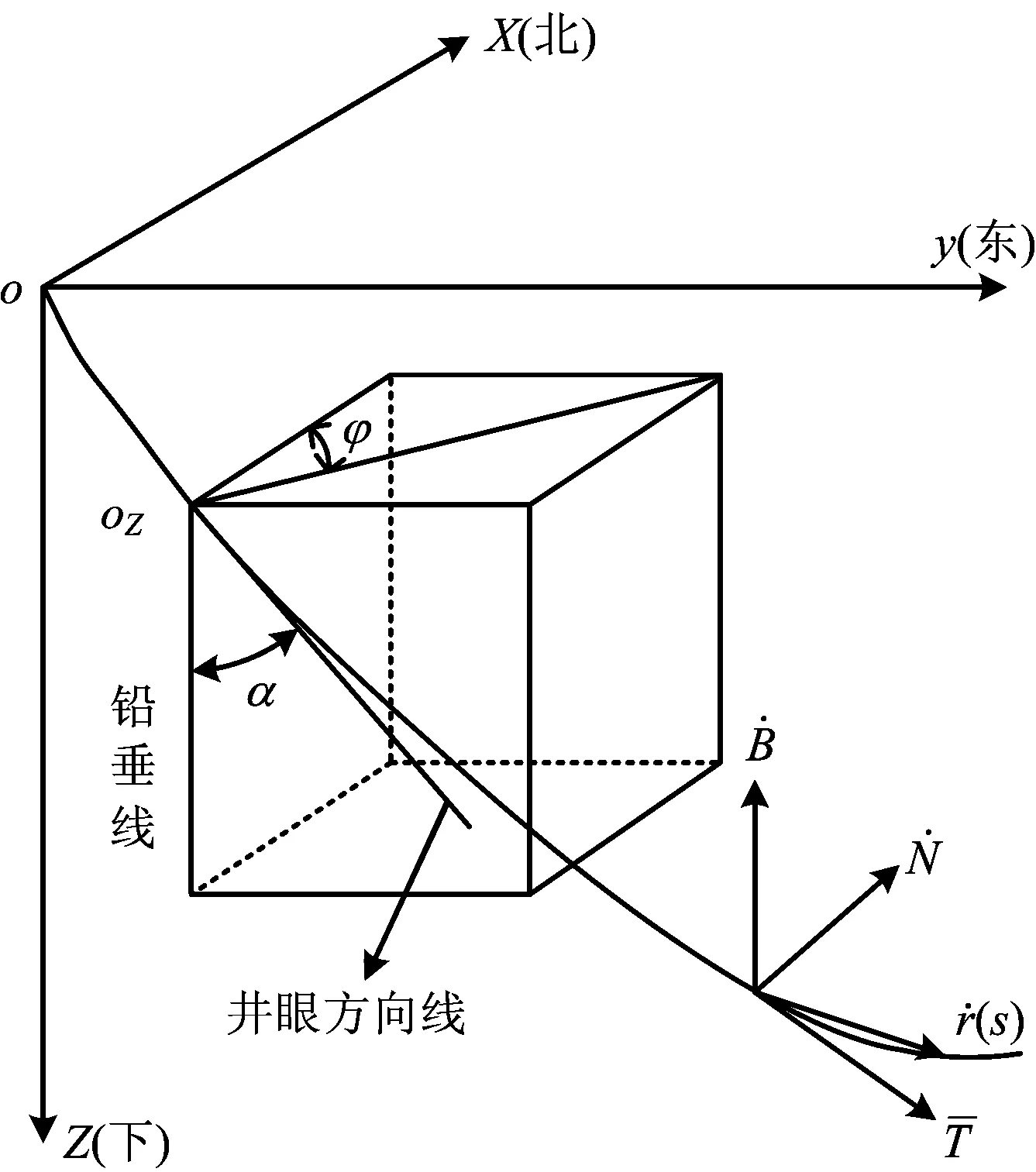
图2 三维井眼轨迹示意Fig.2 Schematic of three dimensional borehole trajectory
螺杆钻具在井底随着井眼轨迹会发生弯曲变形,会受到钻压,扭矩,弯矩的作用,还会受到三维方向复杂作用力的影响,容易发生导致螺杆钻具的传动轴及其接头螺纹容易发生粘扣、疲劳失效甚至断裂,如图3-5所示。

图3 传动轴螺纹端断裂Fig.3 Tread fracture of drive shaft

图4 传动轴轴端断裂Fig.4 Drive shaft fracture

图5 螺纹粘扣Fig.5 Drive shaft thread gluing
2 数值计算
2.1 螺纹有限元模型的建立
由前述分析已知,传动轴上端连接螺纹是传递扭矩和马达水推力的直接作用部位。调研国内不同厂家常用的传动轴上端连接螺纹型号,为便于计算分析,针对公扣与母扣之间的配合关系,根据传动轴连接螺纹相关设计尺寸,内、外螺纹螺距为6 mm,导程为6 mm[18],建立带螺旋升角的三维螺纹有限元模型,如图6所示。

图6 传动轴连接螺纹实体及有限元模型Fig.6 Connection thread material object and finite element model of drive shaft
其中,传动轴材料为42 CrMo高强度钢;弹性模量E=200 GPa;泊松比υ=0.3;其屈服强度σs=951 MPa;密度ρ=7.85×103kg/m3。
边界条件:根据实际工况,将公扣上端面扣底端面固定,在母扣底端面端施加载荷。
2.2 螺纹连接控制方程及计算准则
螺纹连接的有限元控制方程可以表示为[16-17]:
(1)
式中:δεij表示虚应变;xi表示单位表面上的载荷矢量;σij表示欧拉应力张量;s表示面积;δui表示虚位移。
在工作过程中,传动轴上端连接螺纹承受较大的拉压载荷及扭矩,螺纹接触面上产生的应力值会超出材料的屈服极限,因此在进行螺纹接触的有限元计算时,弹性变形和塑性变形都会出现,弹性阶段通常采用Hooked 定理,塑性变形阶段则采用Von Mises屈服准则。传动轴连接螺纹可看作均质金属,屈服后服从Prandtl-Reuss方程,应变增量为:
(2)
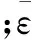
3 有限元结果分析
3. 1 在压缩载荷作用下接头螺纹应力应变的分析
通过有限元计算,螺纹接头分别在60,70,80 t压缩载荷作用下的Von Mises应力如图7所示,随着载荷增加,公母扣所受应力呈现增大的趋势,且公扣端所受到的应力比母扣端应力的大;载荷增大的同时,母扣端最大应力逐渐向内台肩部位转移,而公扣端整体应力分布区域变化较小,当载荷较小时,载荷主要由螺纹承受,随着载荷增加应力逐渐传递给传动轴部分。

图7 不同钻压条件下公母扣应力变化Fig.7 Von Mises Stress variation of pin and box under different bit pressure conditions
由于螺纹为带螺旋升角,三维状态下的受力并不是沿着竖直方向均匀分布的,在轴向载荷作用下产生应力分布较大的区域,螺纹牙为主要的承力单元,致使公母扣螺纹牙啮合的接触压力较大,较大的接触压力会导致传动轴螺纹连接粘扣,与现场拆卸的接头螺纹端粘扣位置相一致(如图5所示),表明在压缩载荷作用下是螺纹粘扣的重要因素。因此安全压缩载荷区间为60~80 t,如图8所示,随着压缩载荷增大,螺纹牙应力增大后变小循环变化,呈现类似正弦规律变化,每一牙在周向上的应力变化并不均匀,且整体偏差较大,在相同压缩载荷下,第1牙的应力大于第2牙应力,载荷但整体偏差较小。在井下工况下,80 t的压缩载荷下螺纹工作应力最大为383.5 MPa,远小于螺纹所受到的屈服强度,因此安全压缩载荷区间为60~80 t。

图10 不同扭矩作用下应力分布Fig.10 Von Mises Stress variation of pin and box under different torque conditions

图8 圆柱面处应力变化曲线Fig.8 Stress variation curve at the cylindrical surface
3.2 扭矩载荷作用下接头螺纹应力应变的分析
通过有限元计算,螺纹接头分别在20,25,30 kN·m扭矩作用下的Von Mises应力云图如图9和图10所示,随着扭矩增大,公母扣所受应力呈现增大的趋势,且公扣端所受到的最大应力为母扣端应力的2倍左右,公扣端靠近台肩圆柱面处的应力较大,螺纹受到的最大应力分别为688.1~822.5 MPa,接近螺纹所受到的屈服强度,公母扣从左往右第1牙、第2牙相对其他螺纹牙应力更大,这是螺纹牙受力较大区域。随着扭矩增大,螺纹牙对应地方的应力逐渐增大,每一牙在周向上的应力变化并不均匀,但整体偏差较小,整体分析扭矩作用下螺纹安全工作区间为20~30 kN·m。
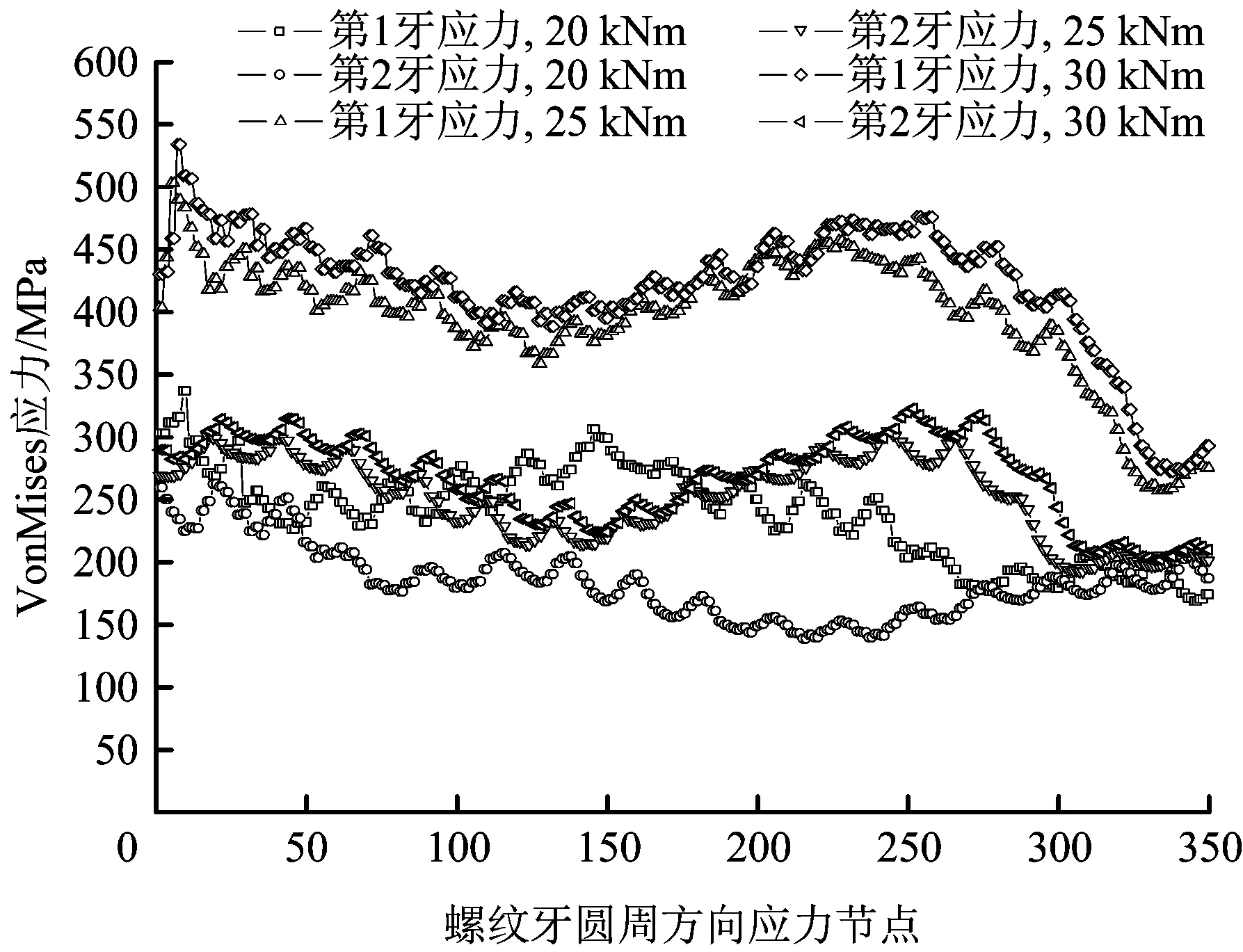
图9 螺纹牙应力变化曲线Fig.9 Stress variation curve at the thread tooth
3.3 弯扭组合作用下接头螺纹应力应变的分析
从图11得到,螺杆钻具在井底随着井眼轨迹会发生弯曲和扭转变形,当螺纹接头在扭矩为25 kN·m,曲率分别为10°/30 m及20°/30 m弯扭组合作用下,随着弯矩增大,公、母扣所受应力呈现增大的趋势,公扣端靠近台肩圆柱面处的应力较大,当扭矩为25 kN·m,曲率为20°/30 m时,最大应力达到972 MPa,超过了传动轴材料的屈服极限(材料屈服极限为951 MPa),此处过大的弯曲应力会直接传递到临近的第1牙及第2牙,在井下恶劣工况作用下更容易发生疲劳断裂,这与实际发生断裂的螺纹对比可以发现,此处连接部分发生了断裂。

图11 弯扭组合作用下应力分布Fig.11 Von Mises Stress of thread under combined bending and torsion conditions
由图12可知,沿着传动轴圆柱面圆周方向取2条路径,其第1、第2路径应力曲线如图12所示,当扭矩为25 kN·m,曲率10°/30 m及20°/30 m应力曲线圆滑过渡,呈现波浪式变化,在波峰处应力相对较大,曲率为20°/30 m时,应力达到972 MPa,超过近材料所承受的屈服极限,长时间处在这种状态下,必然导致传动轴截面破坏。

图12 圆柱面处应力变化曲线Fig.12 Stress variation curve at the cylindrical surface
由图13中第1牙和第2牙的应力曲线比较发现,当曲率为10°/30 m及20°/30 m时,螺纹牙应力分布并不是均匀变化的,且整体曲线为第1牙、第2牙所受的应力随着曲率的增大而增大,呈现先增大后变小并趋于平稳状态,扭矩为25 kN·m,20°/30 m时螺纹牙最大应力达到近900 MPa,虽然未达到材料屈服极限,长期受到此种载荷作用下,螺纹部分会发生疲劳失效,会影响螺纹牙顶的安全性,因此其安全区间在曲率为20°/30 m以下。

图13 螺纹牙应力变化曲线Fig.13 Stress variation curve at the thread tooth
4 结论
1)分别在压缩、扭转、弯扭组合载荷作用下,公扣螺纹端整体受到的应力比母扣螺纹要大3~4倍,且公扣螺纹牙顶受到的应力较其他部位要大一些。
2)通过过有限元分析,压缩载荷作用下螺纹部分应力分布在圆周方向周期性变化,压缩载荷也是连接螺纹粘扣的重要原因。
3)传动轴接头受到弯扭组合作用的影响较大,在公扣台肩面靠近第1牙地方最易发生应力集中现象,长期在这种复合载荷作用下工作,会导致螺纹接头发生屈服破坏,现场断裂情况和有限元分析结果一致。
4)压缩、扭转和弯扭等3种组合载荷下,传动轴接头断裂受到弯扭矩作用的影响最大,其次为扭矩载荷,影响最小的是压缩载荷。这有助于对引起断裂的载荷性质(压缩、扭转、弯扭组合)进行定性和定量判断,为传动轴在井下工作的受力状态提供安全评价基础。
[1] 白鹤,鲁碧为, 何石磊, 等. 拉伸载荷下承载面角度对特殊螺纹接头连接强度影响的有限元分析[J]. 焊管,2015, 38(9):26-31.
BAI He, LU Biwei, HE Shilei, et al. Finite element analysis on the effect of loading flank angle to premium connection tensile strength [J]. Welded pipe and tube,2015, 38(9):26-31.
[2] 袁光杰. API圆螺纹接头力学性能的数值仿真与实验研究[D]. 上海: 上海交通大学,2004.
[3] 高连新, 金烨, 张居勤. 石油套管特殊螺纹接头的密封设计[J]. 机械工程学报,2005,41(3):216-220.
GAO Lianxin, JIN Ye, ZHANG Juqin. Seal design of premium threaded casing connections [J].Chinese Journal of Mechanical Engineering, 2005, 41(3):216-220.
[4] 陈祖志,宋占兵, 石坤, 等.储气井螺纹连接安全性有限元模拟分析及实验研究[J]. 中国安全生产科学技术, 2012,8(10):58-63.
CHEN Zuzhi,SONG Zhanbing,SHI Kun,et al. Experimental study and finite element simulation on safety performance of gas storage well’s thread joint [J]. Journal of Safety Science and Technology, 2012, 8(10):58-63.
[5] 赵金凤,余世杰,袁鹏斌.定向穿越井中外螺纹接头粘扣原因分析[J]. 石油矿场机械,2014, 43(3):63-66.
ZHAO Jinfeng, YU Shijie, YUAN Pengbin. Cause analysis of thread galling on pin joint during directional drilling crossing [J]. Oil field equipment,2014, 43(3):63-66.
[6] 李晓晖,吕拴录,李艳丽,等.钻杆接头粘扣原因分析[J]. 理化检验-物理分册,2016,52(10):746-749.
LI Xiaohui, LYU Shuanlu, LI Yanli, et al. Cases analysis on thread gluing of tool joints [J]. PTCA(Part A:Physical testing),2016,52(10):746-749.
[7] 张攀, 夏换, 周宝库, 等.弯曲变形对钻杆接头螺纹粘扣的影响研究[J]. 石油机械,2013,41(10):21-24.
ZHANG Pan, XIA Huan, ZHOU Baoku, et al. Effects of bending deformation on drill pipe joint thread gluing [J]. China Petroleum Machinery,2013,41(10):21-24.
[8] 王炳英, 薄国公. 螺杆钻具主轴的断裂失效分析[J]. 热加工工艺, 2010,39(14):183-184, 187.
WANG Bingying, BO Guogong. Analysis on fracture failure of screw drill spindle [J]. Hot Working Technology,2010,39(14):183-184,187.
[9] 韩传军, 张杰, 刘洋, 等.螺杆钻具传动轴总成故障树建立及推力轴承应力分析[J]. 矿山机械,2012, 40(10):14-17.
HAN Chuanjun,ZHANG Jie,LIU Yang,et al. Modeling of fault tree of transmission shaft assembly in PDM drill and stress analysis of thrust bearing [J]. Mining & Processing Equipment, 2012, 40(10):14-17.
[10] LIU Yonggang, LIAN Zhanghua, LIN Tiejun, et al. A study on axial cracking failure of drill pipe body [J]. Engineering Failure Analysis, 2016,59:434-443.
[11] 练章华,韩建增, 张毅, 等.套管偏梯形和圆形螺纹滑脱载荷分析[J]. 石油机械,2004,32(5):7-9,49.
LIAN Zhanghua, HAN Jianzeng, ZHANG Yi, et al. Analysis of jump-out loads on connectors of buttress and round threads of casing[J]. CPM, 2004, 32 (5): 7-9,49.
[12] LIN Tiejun, ZHANG Qiang, LIAN Zhanghua, et al. Multi-axial fatigue life prediction of drill collar thread in gas drilling [J]. Engineering Failure Analysis, 2016,59:151-160.
[13] 苏义脑. 螺杆钻具研究及应用[M]. 北京: 石油工业出版社, 2001.
[14] Zhang Jie, Liang Zheng, Han Chuanjun. Failure analysis and finite element simulation of key components of PDM[J]. Engineering Failure Analysis, 2014, 45(45):15-25.
[15] 黄云, 刘清友, 赵华, 等. 一种基于能量法的三维弯曲井眼管柱力学模型研究[J]. 钻采工艺,2012,35(5):80-82.
HUANG Yun,LIU Qingyou,ZHAO Hua,et al. A study on mechanical model of the three dimensional curved hole based on energy method [J]. Drilling&Production Technology, 2012, 35 (5): 80-82.
[16] 祝效华, 高原, 贾彦杰.弯矩载荷作用下偏梯形套管连接螺纹参量敏感性分析[J]. 工程力学,2012, 29(10): 301-307.
ZHU Xiaohua, GAO Yuan, JIA Yanjie. The parameter sensitivity analysis of buttress casing connecting thread under action of bending loading [J]. Engineering Mechanics, 2012, 29(10): 301-307.
[17] SANTUS C, BERTINI L, BEGHINI M, et al. Torsional strength comparison between two assembling techniques for aluminium drill pipe to steel tool joint connection[J]. International Journal of Pressure Vessels and Piping, 2009, 86(2/3): 177-186.
[18] 全国螺纹标准化技术委员会.普通螺纹 直径与螺距标准:GB/T193-2003[S]. 北京:中国标准出版社,2004.
