基于风险熵的化工园区事故风险突变模型研究*
2017-04-16陈国华王永兴高子文
陈国华,王永兴,高子文
(1. 华南理工大学 安全科学与工程研究所,广东 广州 510640;2. 惠州大亚湾应急管理有限公司,广东 惠州 516081)
0 引言
化工园区主要是涉及化工行业的企业聚集区,其危险物质数量和潜在能量巨大[1],企业内部涉及的化学工艺复杂、设备装置众多、操作条件苛刻,稍有疏忽,极易造成严重的事故[2]。能否准确判断事故风险的发展演化过程,直接影响到应急决策方案制定的科学性、有效性及应急救援工作的顺利开展[3]。化工园区事故风险具有动态性和不确定性,如何判断事故风险演化状态并及时采取有效措施,是园区发展中面临的严峻现实。
熵(Entropy)是个源自热力学领域的物理概念,是表示系统无序程度和混乱程度的状态量[4]。风险熵是对系统风险程度不确定性的1种度量[5],常用于系统风险评估、突发事件预测[6],风险熵理论能够从系统风险动态变化的角度分析化工园区事故风险状态和演化方向。国外学者Johnson等[7]研究了熵增与突发事件的关系,指出突发事件发生是系统熵增和紊乱的后果;Spartalis等[8]建立模糊熵的风险评估模型用于自然灾害的风险等级评估。国内学者对熵理论的研究多与脆性理论、耗散结构等结合,用于风险状态的表征,陈伟珂等[9]通过分析熵增因素和负熵因素来说明突发事件的产生机理;汪送等[10]分析风险熵在事故演化网络中的动力学传播过程来为事故分析和预防提供思路。
近年来国内外化工事故不断发生[11],造成众多严重后果。国内外学者从事故多米诺效应[12]、后果模拟[13]、事故发生机理等角度分析了化工事故的发展演化特点。化工园区灾害事故发生过程中系统可能出现崩溃突变的情况,风险熵理论能够在初始事故发生后对系统风险进行研判,以判断是否可能会导致二次事故发生,当前依据风险熵理论分析化工园区事故风险发展演化的研究则较少涉及。
基于以上分析,依据尖点突变模型和风险熵理论,结合化工园区实际情景,构建化工园区系统风险熵突变模型,并对某危化品储存企业丁二烯泄漏情况下园区系统风险状态进行判断,以期为此类事故引发的园区二次事故风险突变提供判别依据和参考。
1 化工园区事故风险跃迁机理分析
化工园区是由物质、能量、信息等汇聚而成的复杂非线性系统,园区内具有众多危险源且与外界环境有相互作用,如图1所示。

图1 化工园区物质、能量、信息流动示意Fig.1 Material, energy and information flow charts in chemical industry parks
系统风险熵与化工园区的风险状态相对应,它有2部分组成,一部分是园区系统内部产生的风险熵增u,熵增会增加系统的紊乱程度;另一部分则是外界输入改善风险的风险熵减v,熵减有利于降低系统风险。
用风险状态参量λ表示化工园区系统风险偏离平衡态的程度,λ=0对应于平衡态,风险状态P是λ的函数,λc为临界状态,当λ<λc时,园区处于系统风险演化初期,风险熵增较少,系统保持稳定状态。当λ>λc,系统越过临界状态进入非线性区,在系统熵增的作用下园区风险状态发生随机“微涨落”,在风险状态临界点(点c,d,e),在突发因素或初始事故的诱发下园区风险状态发生突变[14],产生“巨涨落”,如图2所示,会引起更为严重的后果。

图2 化工园区风险状态跃迁Fig.2 Chemical industry park risk state transition diagram
2 系统风险熵突变模型的原理及构建
2.1 突变模型的原理
突变理论由法国数学家托姆(Renethom)于1972年创立,它通过势函数来描述和预测事物发展过程中的突变。突变模型在社会学、经济学、水资源评价、能源等领域得到广泛应用,常见的有尖点突变模型、燕尾突变模型、蝴蝶突变模型等[15]。突变模型在分析系统的不连续变化过程中不需要涉及到系统的内在机制,其特点是通过势函数来表征系统可能出现的状态,并通过研究参数变化时函数在临界点附近的不连续特征来判断系统是否发生突变。

表1 常用的突变模型
表1中,突变函数F(x1)表示1个系统中状态变量x1的势函数,状态变量系数u1,u2,u3,u4表示该状态变量的控制量。
2.2 化工园区系统风险熵突变模型构建
化工园区是1个复杂的非线性生产系统,将导致系统紊乱程度增加的因素定义为熵增因子,降低系统风险的因素定义为熵减因子,熵增因子和熵减因子相互作用的过程中,风险状态也会发生动态变化,例如火灾爆炸中毒等事故是园区系统风险状态突变的结果,这种状态的突变不是瞬间完成的,而是系统结构、功能朝某个方向演化的结果,当园区有事故征兆或发生初始事故时,通过突变模型对系统风险状态进行判断,以评估二次事故发生的可能性。
2.2.1突变数学模型的选择
化工园区事故风险的动态变化来源于熵增和熵减因子,风险熵增和风险熵减共同决定了事故风险的发展变化过程,由于事故状态是唯一的状态变量,风险熵增和熵减是2个控制变量,对于状态变量个数为1个,控制变量个数为2个,应对应选择表1中的尖点突变模型,用尖点突变理论进行分析,如式1所示。
F(x)=x4+ux2+vx
(1)
式中:x为状态变量,即用于反映园区的系统风险状态;u=fu(u1,u2,…,un)为控制变量,是影响化工园区系统风险状态,促使园区系统风险状态发生突变的因素,即为熵增因子;v=fv(v1,v2,…,vm)为控制变量,是对化工园区紧急情况下采取的各种防控措施降低系统危险程度、降低风险熵以减少事故损失的各种因素,即为熵减因子。
由F′(x)=0,得到风险熵突变模型平衡曲面M的方程为:
4x3+2ux+v=0
(2)
其对应的平衡曲面如图3所示。

图3 系统风险熵尖点突变模型Fig.3 Cusp catastrophe model of system risk entropy
曲面由上、中、下3叶构成,事故状态随状态参量的变化而变化;随着参量的增大,事故的平衡状态由曲面下页的稳定状态逐渐向上叶的事故激发状态移动。
2.2.2熵增和熵减估算模型
化工园区系统风险状态的变化由熵增和熵减因子共同决定,设1个事故场景中共有n个风险熵指标,整个事故的演化发展过程中需要计算的风险熵增(熵减)值的集合为T={A1,A2,…,Ak,…,Am},Ak表示第k时刻的风险熵增(熵减)值(k=1,2,…,m)。分别构建m×n阶熵增矩阵Bg和m×n阶熵减矩阵Bt,如式(3)所示。bg,ki表示第i个风险熵指标第k时刻的风险熵增值(i=1,2,…,n),bt,ki表示第i个风险熵指标第k时刻的风险熵减值(i=1,2,…,n)。
(3)
设ri为事故的演化过程中第i个风险熵指标的权重值(i=1,2,…,n),其中0 (4) 潜在事故发展演化场景各个指标的风险熵增和熵减值可以分别由式(5),(6)求得。 (5) (6) 式中:矩阵F为1×m阶矩阵,且矩阵的每1个元素都为1;gi表示第i个风险熵指标所有时刻熵增值之和,ti表示第i个风险熵指标所有时刻熵减值之和(i=1,2,…,n)。 熵增和熵减值之和由各个指标值根据权重计算得到,由式(7),(8)分别计算系统整体的熵增u和熵减v值。 u=Gu×RT=F×Bg×RT (7) v=Tv×RT=F×Bt×RT (8) 式中:RT为矩阵R的转置矩阵。 2.2.3系统风险状态的判断 对式(2)中的x进行求导,可得事故的临界状态。 F″(x)=12x2+2u=0 (9) 联立式(2),(9)可得系统的分叉集方程C,即平衡曲面上的折痕在控制平面上的投影。 Δ=8u3+27v2=0 (10) 分别根据式(7)和式(8)计算出的整体熵增和熵减,代入判别公式Δ=8u3+27v2判断系统的状态,若Δ>0,化工园区系统风险不被激发,保持稳定状态;若Δ<0,系统风险熵增和风险熵减构成的坐标(u,v)落在分叉集内,系统风险发生突变,化工园区可能存在事故升级的风险;若Δ=0,化工园区系统风险进入临界状态,此时若有不利因素影响可能促使风险状态跃迁到突变状态。 某化工园区现规划使用面积27.8 km2,园区内32家企业构成49个单元的危险化学品重大危险源,生产、 储存、使用、经营和运输过程中涉及到的危险物质共151种,各类危险物质的在线量为5.076 7 Mt,其中最多的危险物质为易燃液体,为4.928 Mt,占石化区危险物质总数的97.07%。这些危险物质广泛存在于企业的生产经营使用全过程中,其中大部分具有易燃易爆、有毒有害等危险特性。 化工园区事故风险状态判断包含6个方面的内容,主要包括突变模型研究、指标参数确定,赋值等方面的内容,具体判断思路如图4所示。 图4 事故风险状态判断思路Fig.4 Accident risk state judgment 根据调研统计,石化产业区储罐数量共计682个,罐容达1 187 178 m3。该石化区危险化学品库房54个,共51 083.1 m2,储存能力25 541.55 t,企业最大储存量5 480.91 t。 3.3.1风险熵指标建立 根据对园区事故风险来源分析可知,园区风险来源于企业内部和企业外部的公共区域,考虑化工园区事故特点和危险物质情况,分为公共区域和企业端,确定风险熵监测指标,并针对一般工艺情况和环境情景给出风险熵指标标准值、低限阈值、高限阈值和指标符号,见表2。 表2 风险熵指标 为了便于数据分析讨论,选择某危化品储存企业丁二烯泄漏情况下对数据进行分析,在监测平台上采集风险监测参数数据,数据采集过程中,分别监测公共区域和企业的端的风险熵指标变化情况,判断泄漏情况下园区事故风险演化状态。 3.3.2指标权重确定方法 在风险熵指标中,不同的指标对于事故演化的重要程度不同,分配的权重系数也不同,并对最终的判断结果有影响,因此要采用合理的方法赋予权重,采用改进的层次分析法[16](AHP)处理专家调查问卷,并计算各风险熵指标权重值。 3.3.3判断矩阵的一致性检验 在层次分析法的应用中,判断矩阵的一致性检验是为了使得到的结论基本合理,根据9个风险熵指标构造了9阶判断矩阵。 1)计算一致性指标CI。 CI=(λmax-n)/(n-1) (11) 式中:λmax为判断矩阵最大特征值;n为判断矩阵阶数。 2)根据表3查找平均随机一致性指标RI值。 3)计算一致性比率CR。 CR=CI/RI (12) 当CR<0.1时,认为判断矩阵具有满意的一致性,可以用于评估,否则需要重新调整判断矩阵。 表3 一致性指标RI值 石化区某危化品存储企业球罐发生丁二烯泄漏事故,该企业采用DCS集散型控制系统,罐区储罐主要工艺参数、全厂的可燃有毒气体检测报警器、火灾报警器引至全厂DCS中心控制室,并同时与园区应急指挥平台相连接。平台监测指标出现明显波动,有可能由泄漏事故引发二次事故,根据企业内和公共区域的监测探头从园区内采集的数据,分为5个时刻分析园区内系统风险熵情况,熵增值的判断主要根据指标检测的波动情况,熵减值的判断主要根据应急措施,系统自适应特性,本质安全设计等。 风险熵指标评分值区间为(-1.00,1.00),其中,熵增的取值区间为(-1.00,0.00),划分为5个等级:特别显著(-1.00,-0.80],比较显著(-0.80,-0.60],显著(-0.60,-0.40],一般(-0.40,-0.20],较小(-0.20,0.00)。相应熵减值的取值区间为(0.00,1.00),也划分为5个等级:较小(0.00, 0.20],一般(0.20,0.40],显著(0.40,0.60],比较显著(0.60, 0.80],特别显著(0.80,1.00),根据每位专家对每1指标不同时刻的等级打分区间取中值再求取它们的平均值(即表4中指标的风险熵增与熵减值),经过检验,专家打分符合一致性要求,然后根据化工园区系统风险熵突变模型进行判断。 表4 园区风险熵值分析 1)权重计算。根据调查问卷,用改进的AHP法计算得到各风险熵指标的权重见表4,其一致性比率CR=0.000 07<0.10,满足一致性要求。 2)事故风险状态判断。由表4数据,根据式(3),(5),(7)可得熵增值u=Gu×RT=P×Bg×RT=-1.503 84。同理根据式(3),(6),(8)可得熵减值v=Tv×RT=P×Bt×RT=0.816 84,带入分叉集方程(10),计算得: Δ=8u3+27v2=-9.192 76<0 可知在丁二烯发生泄漏的情况下化工园区发生了风险状态跃迁突变,系统处于无序崩溃的边缘,此时极易由泄漏事故导致二次事故发生,因此要注意风险管控,及时降低系统风险,防止事故升级。 风险熵指标数值如图5所示。分析显示,在L1(公共区域可燃气体)、L2(公共区域有毒气体)、L3(环境温度)、L4(相对湿度)、L5(风速)、L6(企业端可燃气体)、L7(企业端有毒气体)、L8(罐内温度)、L9(介质液位)等9个指标中, L1,L2,L6,L7指标相对其他指标熵增值较大,对系统风险突变影响较为显著,这是由于丁二烯发生泄漏,企业端和公共区域的可燃气体和有毒气体含量明显增加,监测指标数值发生波动。L6,L7熵减值相对于其他指标也较为明显,可知在发生泄漏事故后企业采取了积极的应急救援防护措施。 图5 风险熵指标数值Fig.5 Numerical value of risk entropy index 图6 各因素占风险熵增比例Fig.6 The ratio of each factor to risk entropy increases 企业端和公共区域所占的风险熵增比例如图6所示。分析表明,企业端是风险熵增的主要因素,可燃有毒气体泄漏很容易导致化工园区系统崩溃,增加二次事故风险突变概率,因此要增加企业内的监测探头,以做到事故的早期预警,配备应急装备物资,提升事故应对能力,加强安全管理和事故隐患排查治理,针对企业可能发生的事故类型定期开展应急演练,由于化工事故具有发展迅速的特点,因此事故的初始阶段是最有利的处置时期。做好特殊情况下园区的应急预案和风险防控措施,有利于将事故消灭在初始阶段,防止二次事故的发生,降低事故损失。 1)借鉴风险熵理论,将风险熵引入化工园区风险分析,提出化工园区事故风险跃迁概念,分析其形成机理。分析表明,化工园区事故风险的动态性和不确定性来源于熵增和熵减因子,风险熵增和熵减共同决定了事故风险的突变演化过程。 2)根据化工园区事故风险特点,结合尖点突变模型,构建化工园区系统风险熵突变模型,结果表明,该模型能对熵增(减)值进行准确的计算,可以为化工园区事故风险判断提供依据。 3)针对某危化品储存企业丁二烯泄漏事故进行分析,并以监测数据为基础,结合问卷调查和专家打分,分析园区风险熵增(减)值,根据计算结果判断化工园区事故风险状态发生突变,有发生二次事故(火灾、爆炸、中毒等)的危险。对各因素进行分析,得出企业端是导致风险熵增的主要因素,据此可提出相应的风险防控措施。 [1]邵辉, 杨丽丹, 李晶. 化工园区重大危险源分级方法研究[J]. 工业安全与环保, 2011, 37(9):12-14. SHAO Hui,YANG Lidan,LI Jing. The study on major hazards ranking for chemical industrial park [J]. Industrial Safety and Environmental Protection, 2011, 37(9):12-14. [2]陈文涛, 葛世友. 基于三角模糊数的化工园区事故应急救援能力评价[J]. 灾害学, 2015,30(2):167-171. CHEN Wentao, GEShiyou. Capability evaluation on emergency response ability for accidents in chemical industry parks based on triangular fuzzy number [J]. Journal of Catastrophology, 2015,30(2):167-171. [3]陈国华, 安霆, 陈培珠. 危险化学品多米诺事故应急资源需求量估算模型[J]. 中国安全科学学报, 2015, 25(4):87-93. CHEN Guohua, AN Ting, CHEN Peizhu. Estimation model of emergency resource demands for chemical accidents involving Domino effect [J]. China Safety Science Journal, 2015, 25(4):87-93. [4]Garrido P L, Goldstein S, Lebowitz J L. Boltzmann entropy for dense fluids not in local equilibrium.[J]. Physical Review Letters, 2003, 92(5):050602. [5]胡瑞敏,吕海涛,陈军.基于风险熵和Neyman-Pearson准则的安防网络风险评估研究[J]. 自动化学报, 2014, 40(12):2737-2746. HU Ruimin, LYU Haitao, CHEN Jun.Risk evaluation model of security and protection network based on risk entropy and Neyman-Pearson criterion[J]. Acta Automatica Sinica, 2014, 40(12):2737-2746. [6]于海峰, 王延章, 卢小丽,等. 基于知识元的突发事件风险熵预测模型研究[J]. 系统工程学报, 2016, 31(1):117-126. YU Haifeng, WANG Yanzhang, LU Xiaoli,et al. Emergency risk entropy forecasting model based on knowledge element[J]. Journal of Systems Engineering, 2016, 31(1):117-126. [7]Johnson IV J J, Tolk A, Sousa-Poza A. A theory of emergence and entropy in systems of systems[J]. Procedia Computer Science, 2013, 20: 283-289. [8]Spartalis S, Iliadis L, Maris F. An innovative risk evaluation system estimating its own fuzzy entropy[J]. Mathematical & Computer Modelling, 2007, 46(46):260-267. [9]陈伟珂, 向兰兰. 基于熵及耗散结构的公共安全突发事件的过程分析研究[J]. 中国软科学, 2007(10):149-154. CHEN Weike, XIANG Lanlan. The process analysis on pubic safety emergencies based on entropy and dissipative structure theory [J]. China Soft Science, 2007(10):149-154. [10]汪送, 王瑛, 杜纯,等. 复杂系统风险熵的涌现与动力学传播分析[J]. 安全与环境工程, 2013, 20(2):118-120,134. WANG Song,WANG Ying, DU Chun,et al. Emergence and dynamic transmission of risk entropy in complex system [J].Safety and Environmental Engineering, 2013, 20(2):118-120,134. [11]李健, 白晓昀, 任正中,等. 2011—2013年我国危险化学品事故统计分析及对策研究[J]. 中国安全生产科学技术, 2014,10(6):142-147. LI Jian,BAI Xiaoyun,REN Zhengzhong,et al. Statistic analysis and countermeasures of hazardous chemicals accidents occurring in China during 2011-2013 [J]. Journal of Safety Science and Technology, 2014,10(6):142-147. [12]Darbra R M, Palacios A, Casal J. Domino effect in chemical accidents: main features and accident sequences.[J]. Journal of Hazardous Materials, 2010, 183(1-3):565-573. [13]凌晓东, 党文义, 于安峰,等. 环己烷泄漏事故模拟与风险控制措施研究[J]. 中国安全生产科学技术, 2013, 9(8):33-39. LING Xiaodong, DANG Wenyi,YU Anfeng,et al. Research on the simulation of cyclohexane leakage accidents and development of risk control measures[J]. Journal of Safety Science and Technology,2013, 9(8):33-39. [14]凌复华. 突变理论及其应用[M]. 上海:上海交通大学出版社, 1987. [15]苗东升. 系统科学大学讲稿[M]. 北京:中国人民大学出版社, 2007. [16]陈国华, 梁韬, 张华文. 城域承灾能力评估研究及其应用[J]. 安全与环境学报, 2008, 8(2):156-162. CHEN Guohua, LIANG Tao, ZHANG Huawen. Evaluation model for urban-regional disaster-bearing capacity and its application[J]. Journal of Safety and Environment, 2008, 8(2):156-162.3 化工园区事故风险突变实例分析
3.1 某化工园区概况
3.2 化工园区事故风险突变判断思路

3.3 风险熵指标体系构建


3.4 事故风险突变分析
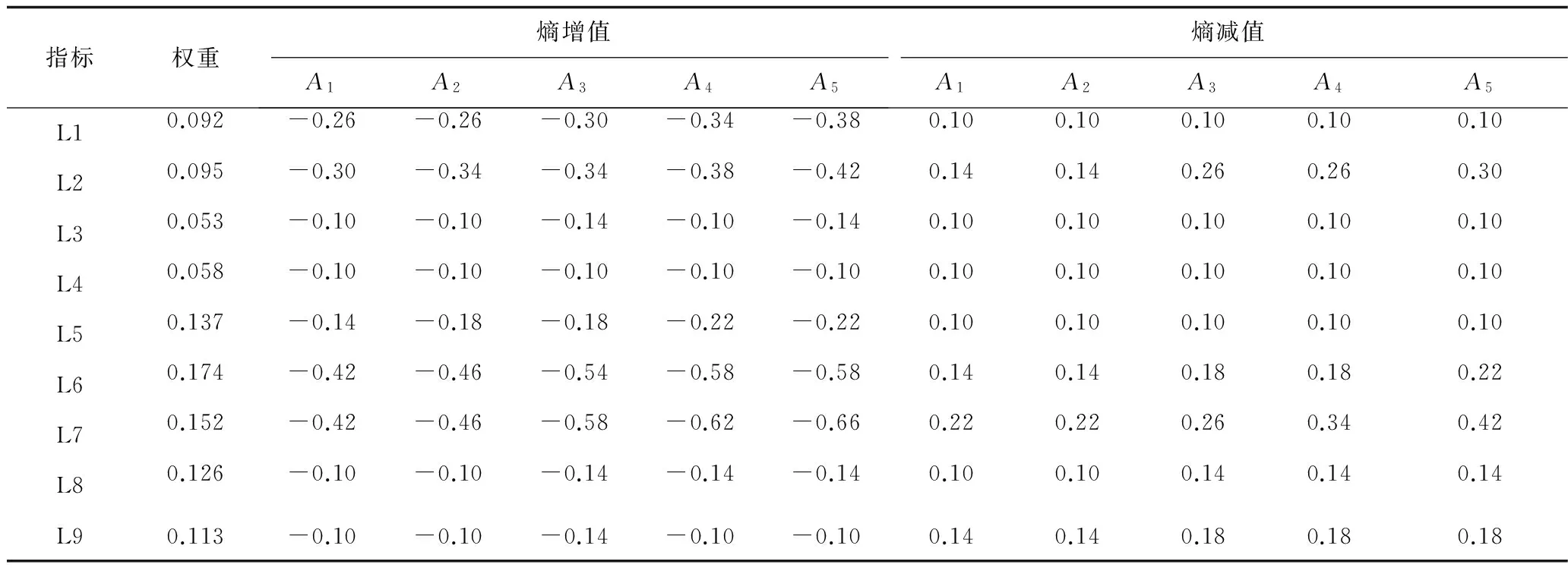
3.5 分析与建议


4 结论
