进化算法求解背包问题研究

黄林峰

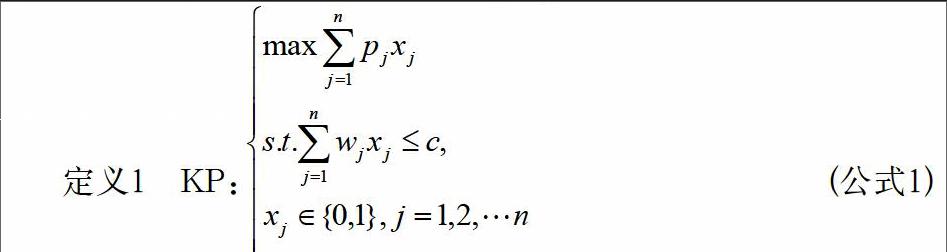
摘要：01背包问题（Knapsack Problem）是运筹学中一个经典的优化难题，在现实生活中有着非常广泛的实际应用背景（如预算控制、货物装载、项目选择等）。背包问题的求解算法很多，进化计算作为其中的一种，具有不依赖于初始群体的全局搜索能力，比较适合用来求解背包问题。本文研究了利用进化算法求解背包问题的具体实现，对于现实中背包问题实际应用的求解有重要的意义。

关键词：背包问题 进化算法 进化策略

中图分类号：TP181 文献標识码：A 文章编号：1007-9416（2016）12-0142-01

1 进化算法简介

进化算法（Evolutionary Algorithms，简称EA）也称为进化计算（Evolutionary Computation，简称EC）[1]，是基于自然界中的进化策略，模拟自然生物进化而形成的自适应全局优化搜索算法。它以一个初始种群为对象，通过随机选择种群中个体进行重组、变异来产生新的个体。这些个体根据适应能力强弱而被选择或淘汰，被选择的个体形成新一代种群。重组、变异、选择组成了进化算法的三个基本操作。个体编码，适应度函数计算等是进化算法的重要内容。基于对生物进化的模拟，共产生了三种典型的进化算法模型：

（1）遗传算法（Genetic Algorithms，简称GA）；

（2）进化策略（Evolution Strategy，简称ES）；

（3）进化规划（Evolutionary Programming，简称EP）。

这些进化模型基于不同的生物进化背景，有不同的侧重点，它们的进化框架是一样的，只是在具体的重组、变异或选择算子上有所不同。

2 背包问题定义

背包问题（KP）是运筹学中一个典型的优化难题，在现实生活中有着广泛的实际应用背景（如预算控制、货物装载、项目选择等），基本的0/1背包问题的形式化定义如下[2]。

其中，n为所有物品的数目，pj和wj分别为第j个物品的价值和重量分别，c为背包的容量。背包问题的目标就是从给定物品的集合中选出一个子集，使得选中的所有物品的价值和最大，但是重量和不能超过背包的容量c。

3 进化算法求解背包问题框架

进化算法是一种启发式的群体搜索算法，符合达尔文“适者生存”和随机信息交换的思想。进化算法与传统优化方法相比具有不依赖于初始群体的全局搜索能力等多方面的优势，因此被广泛的用来求解现实中的各种优化问题，其中包括背包问题。图1给出了进化算法求解背包问题的伪代码。

4 结语

背包问题是一种NP难解问题，不存在多项式时间算法能求得其精确解，进化算法由于其自身特点比较适合用来求解背包问题，并得到了很多具体的应用。

参考文献

[1]Deb K. Multi2Objective Optimization Using Evolutionary Algorithms. Chicester， UK： JohnWiley & Sons， 2001.

[2]Hans Kellerer Ulrich Pferschy， David Pisinger. Knapsack Problems， Springer-Verlag Berlin，2004.