基于遗传算法的岩土及填料热物性参数评估

张泉+马小威+张林锋

摘 要：岩土及填料的热物性参数可直接影响地埋管换热器的性能设计.针对现场热响应测试中填料热物性参数需要预先测量，而无法通过计算直接评估的难题，在无限长线热源模型及管壁热阻修正复合介质线热源模型的基础上，应用遗传算法对岩土及填料的热物性参数同时进行评估，并结合热响应测试实验，验证了该方法的准确性.钻孔热阻、岩土导热系数和填料导热系数的评估值与实测值的相对误差分别为3.47%，1.42%和4.93%.2种模型计算所得流体平均温度与实测值的均方根误差分别为0.050 5 ℃和0.172 ℃.研究结果对地埋管换热器的设计具有重要参考价值.

关键词：填料热物性；遗传算法；复合介质线热源；热响应

中图分类号：TU831.6 文献标志码：A

文章编号：1674-2974（2017）03-0151-06DOI：10.16339/j.cnki.hdxbzkb.2017.03.019

Abstract：The parameters for thermal properties of ground and grout have directly effect on the performance of ground heat exchanger （GHE）. For the problem that grout thermal properties of in-situ thermal response test （TRT） need to be measured in advance and cannot be evaluated directly by calculation， this paper applied genetic algorithm to evaluate the parameters of ground and grout thermal properties simultaneously on the basis of infinite line source （ILS） model and composite media line source （CMLS） model with wall thermal resistance correction. The method was validated by in situ TRT. Compared with the measured values， the calculation relative error of borehole thermal resistance， ground thermal conductivity and diffusivity was 3.47%， 1.42% and 4.93%， respectively. The root mean square error （RMSE） of the calculated average temperature by these two models and the measured value is 0.0505 and 0.172 ℃， respectively. The results provide important reference for GHE design.

Key words：grout thermal properties；genetic algorithms；composite media line source；thermal response test

岩土及填料的热物性参数是地埋管换热器设计的关键参数，准确地评估岩土及填料的热物性参数可以解决地埋管换热器设计不当的问题.目前，岩土热物性参数主要采用斜率法和参数估计法进行评估计算.相比于斜率法，参数估计法可有效降低测试中热流不恒定对评估参数值的影响，其评估精度较高[1].因此，在ASHRAE手册中，推荐采用参数估计法进行岩土热物性参数的评估[2].

参数估计法评估岩土热物性参数是一个典型的逆传热问题.该方法以岩土热物性参数为决策变量，以各时刻流体平均温度的计算值和实测值的平方和误差（SSE）或均方根误差（RMSE）为目标函数，通过最小化寻优算法求解岩土热物性参数.但目前所采用的参数估计法存在以下2个方面的问题：1） 主要运用单纯形法、模式搜索法等算法寻优求解[3]，其收敛速度较慢，并受迭代初值的影响，导致评估结果可能存在较大误差.2） 参数估计法评估岩土热物性参数时，常以钻孔壁温度为计算耦合点，忽略了钻孔内填料的热物性，无法采用参数估计模型直接评估填料热物性参数.

为克服参数估计法的上述缺点，本文结合地埋管无限长线源模型和管壁热阻修正的复合介质线热源模型，利用遗传算法同时评估钻孔热阻、岩土导热系数和热扩散系数以及填料导热系数和热扩散系数等5个参数，并结合热响应测试实验，验证了该方法的准确性.

1 地埋管传热模型

1.1 无线长线热源模型

Kelvin[4]提出了竖直地埋管钻孔外一维无限长线热源传热模型，该模型通过钻孔壁温度耦合钻孔内稳态导热和钻孔外非稳态导热.当传热时间大于10 h时，通过该简化模型可求得流体平均温度为[5-6]：

1.2 复合介质线热源模型

在无限长线热源模型的基础上，Li等[7]提出了一种全时间范围内的地埋管温度响应G函数模型.该模型将U型管管壁作为温度耦合点，以U型管外壁面A和B两点的平均温度代表U型管管壁的平均温度，如图1所示.

复合介质线热源模型由于考虑了填料热容和钻孔埋管几何尺度对换热性能的影响，在一定时间范围内，可较准确地计算流体平均温度.

2 基于遺传算法的热物性参数评估

遗传算法（Genetic Algorithm）是一种模仿自然界生物进化，并带有随机性的全局搜索方法.该算法由可能潜在解集的种群开始计算，通过优胜劣汰的准则产生适应度较高的解集（种群），在每一代进化过程中，选择种群中适应度水平较高的个体进行交叉重组以及变异，并产生子种群，由此通过一定代数的进化即可得到最优解的个体[10].与传统优化算法相比，遗传算法具有较好的全局收敛性、计算速度快、不受目标函数的约束、可并行计算等诸多优点，在工程计算中得到了广泛应用.

本文遺传算法采用谢菲尔德大学所开发的Matlab遗传算法工具箱（gatbx）[11].求解中，设定钻孔热阻Rb，岩土导热系数λs，岩土热扩散系数as，填料导热系数λb和填料热扩散系数ab等5个参数为决策变量.以式（1）和式（6）计算所得的流体平均温度与实测值的综合均方根误差为目标函数[12]，如式（7）所示.该目标函数最小时所对应的决策变量即为最终评估结果.

式中：Tf，ILS为无限长线热源模型计算的各时刻流体平均温度，℃；Tf，CMLS为复合介质线热源模型计算的各时刻流体平均温度，℃；Tf，EX为实测各时刻流体平均温度，℃，计算中取各时刻U型管流体进出口温度的算术平均值；n为用于无限长线热源模型计算的测量数据组数；m为用于复合介质线热源模型计算的测量数据组数.

在算法优化过程中，几个关键遗传操作设置如下：

1）编码：为提高算法效率和求解精度，本文采用实数型编码的方式对种群进行编码.

2）适应度函数：目标函数至适应度函数的转换，采用非线性排序算法且选择压差为2[11].

3）交叉：采用随机遍历抽样（SUS）选择父体进行交叉运算.由于采用实数型编码，交叉概率的取值不影响离散重组产生子代个体的表征，故将其设为1[11].

4）变异：为防止算法局部收敛，变异运算采用自适应算法[13].

5）迁移：在子种群迁移中，将子种群定义成网状结构，并根据其适应度值进行各子种群间的个体迁移[14].

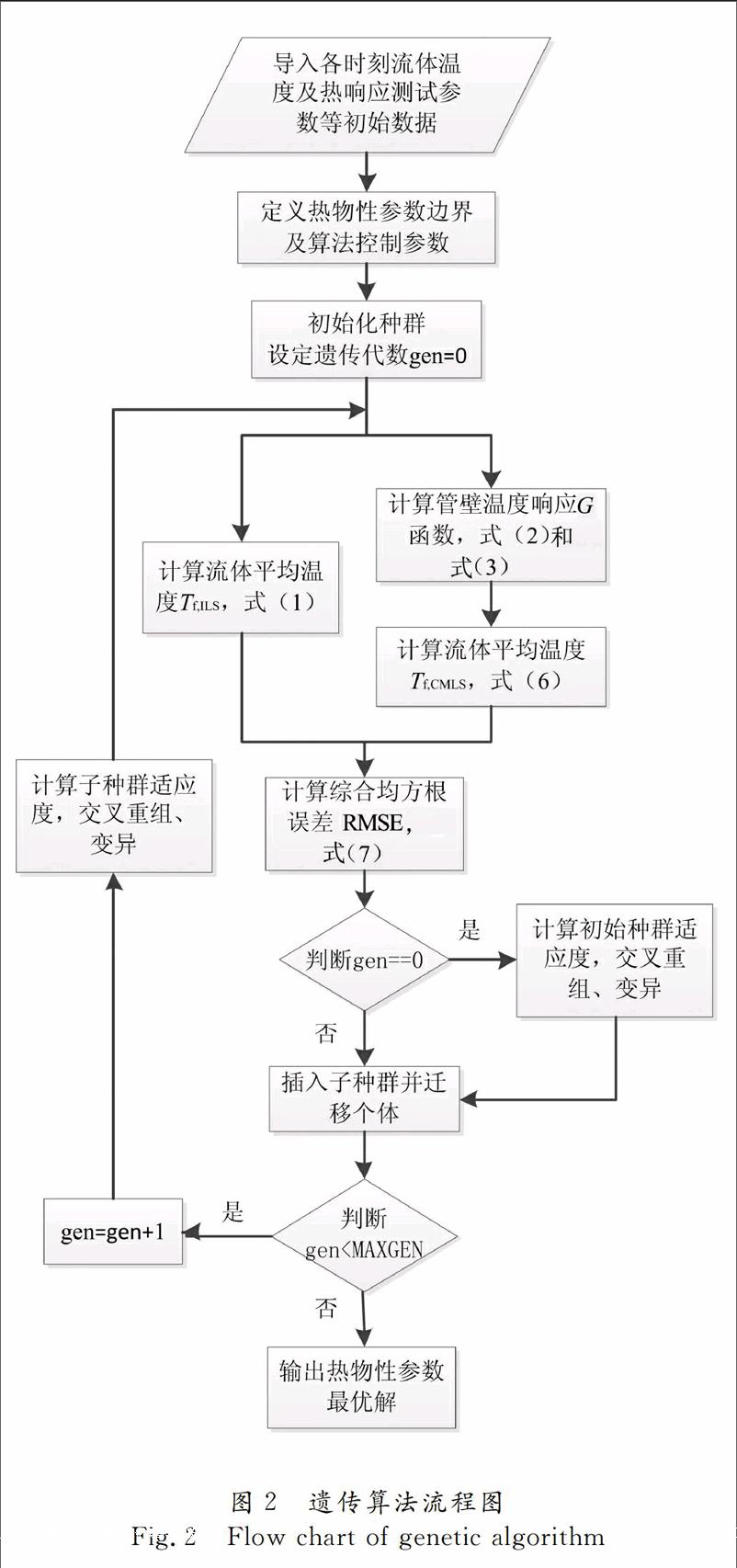
算法中各控制参数设置及优化流程分别如表1和图2所示.

3 算法应用及分析

3.1 沙箱热响应测试

Beier等[15]在实验室中搭建了一个较大的沙箱（sandbox）进行热响应测试实验.沙箱周围采用木板结构固定，里面填充潮湿沙土，其长和宽分别为18.32 m和1.83 m.中心处设置内径为12.6 cm的铝管构建钻孔壁，其内水平安装单U型地埋管换热器，并用质量分数为20%的泥浆膨润土进行回填.

热响应测试实验中利用2台电加热器对流体进行加热，加热器输入功率不确定性为±1%；热敏电阻测量U型管进出口流体温度，其测量不确定性为±0.03 ℃；流量计测量流体体积流量，其测量不确定性为±5%.总测试时长为48 h，其主要测试参数见表2.

3.2 目标函数进化

图3给出了综合均方根误差（RSME）最小值及平均值随遗传代数的变化.可以看出，目标函数（综合均方根误差）在40代以后变化较缓，此时计算收敛，最小值和平均值分别为0.111和0.118 ℃.

当目标函数最小时，2个模型分别计算所得的均方根误差遗传代数的变化如图4所示.当算法逐渐收敛之后，复合介质线热源模型计算所得均方根误差比无限长线热源模型大，收敛之后其差异平均值为0.124 ℃.这是因为采用复合介质模型计算流体平均温度时，未舍去热响应测试前10 h的温度数据，其计算时长即为热响应测试总时长.由于传热前期钻孔内非稳态传热对流体温度的影响较大，根据复合介质模型计算的流体平均温度和实际值的温度差也相应较大.

3.3 参数评估结果及分析

基于地埋管无限长线源模型和管壁热阻修正的复合介质线热源模型，分别采用模式搜索法（Hooke-Jeeves算法）、单纯形法和遗传算法进行岩土及填料热物性参数评估，结果见表3.表中钻孔热阻的实测值是通过单独测量钻孔壁平均温度计算所得.模式搜索法由初始值开始交替实施轴向搜索和模式搜索，直至找到最优值.单纯形算法则是基于线性规划问题的可行域多面凸集原理，通过查找该凸集的某顶点得出最优值.可以发现，遗传算法计算所得的综合均方根误差最小，为0.111 ℃，且钻孔热阻和导热系数的评估相对误差均小于5%.

图5所示为综合均方根误差最小时所对应的流体平均温度随时间的变化曲线.由图可知，模型计算流体平均温度与实测值均吻合较好，所得流体平均温度与实测值的均方根误差分别为0.0505和0.172 ℃.同时可见，复合介质模型计算流体平均温度与实测值的差异主要集中在前10 h以内.

4 结 论

本文采用管壁热阻修正的复合介质线热源模型与无限长线热源模型并联求解流体平均温度，并以流体平均温度的综合均方根误差为目标函数，采用自适应变异型多种群遗传算法寻优求解了钻孔热阻、岩土导热系数及热扩散系数、填料导热系数及热扩散系数等5个热物性参数.与传统参数估计法相比，通过管壁热阻修正复合介质线热源模型可较准确地计算流体平均温度，同时可评估填料热物性参数.在沙箱热响应测试中应用遗传算法进行岩土及填料热物性参数评估，通过计算可以得出以下结论：

1）寻优过程中，遗传进化到40代左右时计算收敛，所得最终均方根误差的最小值为0.111 ℃.

2）与其他寻优算法相比，应用遗传算法评估岩土及填料的热物性参数，精度较高，钻孔热阻、岩土导热系数、填料导热系数的相对误差分别为3.47%，1.42%和4.93%.

3）通过评估所得岩土及填料热物性参数计算流体平均温度，与实测值相比，根据线热源模型和复合模型计算所得流体平均温度的均方根误差分别为0.050 5 ℃和0.172 ℃.

参考文献

[1] SPITLER J D，GEHLIN S E A. Thermal response testing for ground source geat pump systems-an historical review[J]. Renewable and Sustainable Energy Reviews，2015， 50：1125-1137.

[2] ASHRAE. ASHRAE handbook： HVAC applications [M]. Atlanta，GA： American Society of Heating，Refrigerating and Air-Conditioning Engineers，Inc， 2011：34.13-34.17.

[3] ZHANG C，GUO Z， LIU Y， et al. A review on thermal response test of ground-coupled heat pump systems[J]. Renewable and Sustainable Energy Reviews，2014，40（8）：851-867.

[4] KELVIN T W. Mathematical and physical papers II[M]. London：Cambridge University Press，1884：41-60.

[5] 刁乃仁，方肇洪.地埋管地源热泵技术[M].北京：高等教育出版社，2006：47-50.

DIAO Nairen，FANG Zhaohong.Ground-coupled heat pump technology [M]. Beijing：Higher Education Press，2006：47-50.（In Chinese）

[6] ZHANG L F，ZHANG Q，HUANG G S，et al. A P（t）-linear average method to estimate the thermal parameters of the borehole heat exchangers for in situ thermal response test[J]. Applied Energy，2014，131（7）：211-221.

[7] LI M，LI P，CHAN V，et al. Full-scale temperature response function （G-function） for heat transfer by borehole ground heat exchangers （GHEs） from sub-hour to decades [J]. Applied Energy，2014，136：197-205.

[8] LI M， LAI A C K. Analytical model for short-time responses of ground heat exchangers with U-shaped tubes： Model development and validation [J]. Applied Energy，2013，104：510-516.

[9] ZHANG L F，ZHANG Q，HUANG G S. A transient quasi-3D entire time scale line source model for the fluid and ground temperature prediction of vertical ground heat exchangers[J]. Applied Energy，2016，170：65-75.

[10]张泉，杜亚星，张林峰，等. 基于遗传算法的单U地源热泵钻孔内热阻研究[J]. 湖南大学学报：自然科学版，2014，41（9）：100-105.

ZHANG Quan，DU Yaxing，ZHANG Linfeng，et al. A study on the heat resistance of single U pipe in the ground source heat pump system based on genetic algorithm[J].Journal of Hunan University： Natural Sciences， 2014，41（9）：100-105. （In Chinese）

[11]ANDREW C，PETER F，HARTMUT P，et al. Genetic algorithm TOOLBOX for use with MATLAB，users guide v1.2[R]. Sheffield：University of Sheffield，2003：9-36.

[12]FUJII H，OKUBO H，NISHI K，et al. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers [J]. Geothermics，2009，38（4）：399-406.

[13]SRINIVAS M，PATNALK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on Systems，Man and Cybernetics，1994，24（4）：656-667.

[14]雷英杰.MATLAB遺传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005：68-69.

LEI Yingjie. Genetic algorithm toolbox and application[M].Xian：Xidian University Press，2005：68-69. （In Chinese）

[15]BEIER R A，SMITH M D，SPITLER J D. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis [J]. Geothermics，2011，40（1）：79-85.